[SDOI2009]HH的项链 题解
题目地址:洛谷:【P1972】[SDOI2009]HH的项链 – 洛谷、BZO …
May all the beauty be blessed.
题目地址:洛谷:【P1110】[ZJOI2007]报表统计 – 洛谷、BZOJ:Problem 1058. — [ZJOI2007]报表统计
Q的妈妈是一个出纳,经常需要做一些统计报表的工作。今天是妈妈的生日,小Q希望可以帮妈妈分担一些工作,作为她的生日礼物之一。
经过仔细观察,小Q发现统计一张报表实际上是维护一个非负整数数列,并且进行一些查询操作。
在最开始的时候,有一个长度为N的整数序列,并且有以下三种操作:
INSERT i k:在原数列的第i个元素后面添加一个新元素k;如果原数列的第i个元素已经添加了若干元素,则添加在这些元素的最后(见下面的例子)
MIN_GAP:查询相邻两个元素的之间差值(绝对值)的最小值
MIN_SORT_GAP:查询所有元素中最接近的两个元素的差值(绝对值)
例如一开始的序列为5 3 1
执行操作INSERT 2 9将得到:5 3 9 1
此时MIN_GAP为2,MIN_SORT_GAP为2。
再执行操作INSERT 2 6将得到:5 3 9 6 1
注意这个时候原序列的第2个元素后面已经添加了一个9,此时添加的6应加在9的后面。这个时候MIN_GAP为2,MIN_SORT_GAP为1。
于是小Q写了一个程序,使得程序可以自动完成这些操作,但是他发现对于一些大的报表他的程序运行得很慢,你能帮助他改进程序么?
输入格式:
第一行包含两个整数N,M,分别表示原数列的长度以及操作的次数。
第二行为N个整数,为初始序列。
接下来的M行每行一个操作,即“INSERT i k”,“MIN_GAP”,“MIN_SORT_GAP”中的一种(无多余空格或者空行)。
输出格式:
对于每一个“MIN_GAP”和“MIN_SORT_GAP”命令,输出一行答案即可。
输入样例#1:
3 5 5 3 1 INSERT 2 9 MIN_SORT_GAP INSERT 2 6 MIN_GAP MIN_SORT_GAP
输出样例#1:
2 2 1
对于30%的数据,N ≤ 1000 , M ≤ 5000
对于100%的数据,N , M ≤500000
对于所有的数据,序列内的整数不超过5×10^8。
我们只需要记下原数列中某元素对应的序列的头与尾以及全局和差分分别开一个multiset就能解决本题。
插入一个元素的时候,用该元素与插入序列的尾及后一个序列的头的差更新差分multiset,并且从全局multiset中找到lower_bound位置,计算MIN_SORT_GAP即可。
// Code by KSkun, 2018/4
#include <cstdio>
#include <algorithm>
#include <set>
inline int abs(int x) {
return x >= 0 ? x : -x;
}
inline int min(int a, int b) {
return a < b ? a : b;
}
const int MAXN = 500005, INF = 1e9;
int n, m, x, k, msg = INF;
char op[30];
int a[MAXN][2];
std::multiset<int> glo, del;
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
scanf("%d", &x);
a[i][0] = a[i][1] = x;
glo.insert(x);
if(i > 1) del.insert(abs(a[i][0] - a[i - 1][0]));
}
for(std::multiset<int>::iterator it = ++glo.begin(); it != glo.end(); it++) {
msg = min(msg, *it - *--it); it++;
}
while(m--) {
scanf("%s", op);
if(op[0] == 'I') {
scanf("%d%d", &x, &k);
if(x < n) del.erase(del.find(abs(a[x][1] - a[x + 1][0])));
del.insert(abs(k - a[x][1]));
a[x][1] = k;
if(x < n) del.insert(abs(a[x][1] - a[x + 1][0]));
std::multiset<int>::iterator pre = glo.lower_bound(k);
if(pre != glo.end()) msg = min(msg, *pre - k);
if(pre != glo.begin()) msg = min(msg, k - *--pre);
glo.insert(k);
} else if(op[4] == 'G') {
printf("%d\n", *del.begin());
} else {
printf("%d\n", msg);
}
}
return 0;
}
题目地址:洛谷:【P2146】[NOI2015]软件包管理器 – 洛谷、BZOJ:Problem 4196. — [Noi2015]软件包管理器
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入格式:
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式:
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
输入样例#1:
7 0 0 0 1 1 5 5 install 5 install 6 uninstall 1 install 4 uninstall 0
输出样例#1:
3 1 3 2 3
输入样例#2:
10 0 1 2 1 3 0 0 3 2 10 install 0 install 3 uninstall 2 install 7 install 5 install 9 uninstall 9 install 4 install 1 install 9
输出样例#2:
1 3 2 1 3 1 1 1 0 1
n,q<=10000
考虑安装软件包即安装从根0到该点的路径上的所有软件包,则先求和算出改变数再链改值。卸载软件包即卸载其子树中所有软件包,则先求和算出改变值再子树改值。
由于0号点不好处理,我们给点的编号加1。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline int readop() {
char c;
int res = 1;
while(!isalpha(c = fgc()));
while(isalpha(c)) {
if(c == 'u') res = 2;
c = fgc();
}
return res;
}
const int MAXN = 1000005;
int n, dfn[MAXN], ptn[MAXN];
std::vector<int> gra[MAXN];
// Segment Tree
#define lch o << 1
#define rch (o << 1) | 1
#define mid ((l + r) >> 1)
int val[MAXN << 2], tag[MAXN << 2];
inline void pushdown(int o, int l, int r) {
if(tag[o] != -1) {
tag[lch] = tag[rch] = tag[o];
val[lch] = tag[o] * (mid - l + 1);
val[rch] = tag[o] * (r - mid);
tag[o] = -1;
}
}
inline void merge(int o) {
val[o] = val[lch] + val[rch];
}
inline void modify(int o, int l, int r, int ll, int rr, int v) {
if(l >= ll && r <= rr) {
val[o] = v * (r - l + 1);
tag[o] = v;
return;
}
pushdown(o, l, r);
if(ll <= mid) modify(lch, l, mid, ll, rr, v);
if(rr > mid) modify(rch, mid + 1, r, ll, rr, v);
merge(o);
}
inline int query(int o, int l, int r, int ll, int rr) {
if(l >= ll && r <= rr) {
return val[o];
}
pushdown(o, l, r);
int res = 0;
if(ll <= mid) res += query(lch, l, mid, ll, rr);
if(rr > mid) res += query(rch, mid + 1, r, ll, rr);
return res;
}
int fa[MAXN], siz[MAXN], dep[MAXN], top[MAXN], son[MAXN], clk;
inline void dfs1(int u) {
siz[u] = 1;
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(v == fa[u]) continue;
fa[v] = u;
dep[v] = dep[u] + 1;
dfs1(v);
siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
}
inline void dfs2(int u, int tp) {
dfn[u] = ++clk;
ptn[dfn[u]] = u;
top[u] = tp;
if(son[u]) {
dfs2(son[u], tp);
}
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline void modify(int x, int y, int z) {
int tx = top[x], ty = top[y];
while(tx != ty) {
if(dep[tx] > dep[ty]) {
std::swap(x, y);
std::swap(tx, ty);
}
modify(1, 1, n, dfn[ty], dfn[y], z);
y = fa[ty];
ty = top[y];
}
if(dep[x] > dep[y]) {
std::swap(x, y);
}
modify(1, 1, n, dfn[x], dfn[y], z);
}
inline int query(int x, int y) {
int tx = top[x], ty = top[y];
int res = 0;
while(tx != ty) {
if(dep[tx] > dep[ty]) {
std::swap(x, y);
std::swap(tx, ty);
}
res += query(1, 1, n, dfn[ty], dfn[y]);
y = fa[ty];
ty = top[y];
}
if(dep[x] > dep[y]) {
std::swap(x, y);
}
res += query(1, 1, n, dfn[x], dfn[y]);
return res;
}
inline void modify(int x, int z) {
modify(1, 1, n, dfn[x], dfn[x] + siz[x] - 1, z);
}
inline int query(int x) {
return query(1, 1, n, dfn[x], dfn[x] + siz[x] - 1);
}
int q, op, x;
int main() {
memset(tag, -1, sizeof(tag));
n = readint();
for(int i = 2; i <= n; i++) {
x = readint() + 1;
gra[x].push_back(i);
gra[i].push_back(x);
}
dfs1(1);
dfs2(1, 1);
q = readint();
while(q--) {
op = readop(); x = readint() + 1;
if(op == 1) {
printf("%d\n", dep[x] + 1 - query(1, x));
modify(1, x, 1);
} else {
printf("%d\n", query(x));
modify(x, 0);
}
}
return 0;
}
题目地址:BZOJ:Problem 5146. — 有趣的概率
“可爱的妹子就像有理数一样多,但是我们知道的,你在数轴上随便取一个点取到有理数的概率总是0,”芽衣在床
上自顾自的说着这句充满哲理的话,”诶,柚子,我写完概率论的作业你就和我出去约会怎么样””好呀,但是你要
做完才可以哦”柚子回答道,芽衣立刻从床上翻下来冲到了座位上,诶,就一道题啊,真好,题目是这样的:在一
个圆上任取n个点,求由这n个点依次围成的凸n边形至少有一个锐角的概率是多少,芽衣急于和柚子去约会,当然
没有心情想这一道题,于是她就来求助聪明的你啦。
输入格式:
一个n,4<=N<=10000000000
输出格式:
至少有一个锐角的概率,为了避免精度问题,对1e9+7取模
输入样例#1:
136865353
输出样例#1:
423626558
参考资料:【bzoj5146】有趣的概率 微积分 – GXZlegend – 博客园
这个凸多边形的一个锐角的一个邻角必然是钝角,而这个钝角在锐角的逆时针方向的组合只会有一种。我们只研究这两个角。
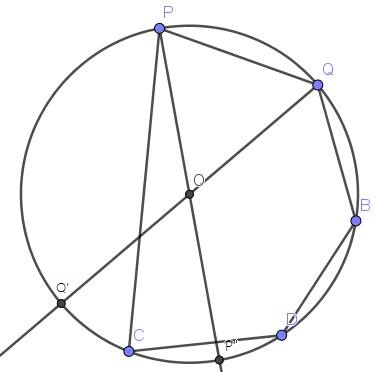
我们看锐角P与钝角Q,设\angle POQ = 2 \pi x,显然这个凸多边形至少有一个点在弧\overgroup{QP'}上,且所有点都分布在弧\overgroup{Q'PQ}上。因此,除了P、Q外其他n-2个点合法的概率为都在弧\overgroup{Q'PQ}上的概率减去都在\overgroup{P'Q'}上的概率,为 (\frac12)^{n-2} - x^{n-2} 。由于x是一个连续的随机变量,我们需要积分出最后的概率。x \in [0, \frac12],故上述概率为\int_0^{\frac12}((\frac12)^{n-2}-x^{n-2})\mathrm{d}x = \frac{n-2}{n-1}(\frac12)^{n-1}。
注意上述概率是有顺序的,换句话说就是剩余n-2个点的标号已经确定,因此还需要枚举P与Q的标号,即最后的答案是n(n-1) \cdot \frac{n-2}{n-1}(\frac12)^{n-1} = n(n-2)(\frac12)^{n-1}。
注:有标号的意义可以理解为组合数和排列数的区别,即每个点都是不同的,即使它们忽略不同点的分布一致,也视作不同的情况。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MO = 1e9 + 7;
inline LL fpow(LL n, LL k) {
LL res = 1;
while(k) {
if(k & 1) res = res * n % MO;
n = n * n % MO;
k >>= 1;
}
return res;
}
LL n;
int main() {
n = readint() % MO;
printf("%lld\n", n * (n - 2) % MO * fpow(fpow(2, n - 1), MO - 2) % MO);
return 0;
}