[CSP-S2 2019]树的重心 题解
题目地址:洛谷:P5666 树的重心 – 洛谷 | 计算机科学教育新生态 题目 …
May all the beauty be blessed.
题目地址:洛谷:P5659 树上的数 – 洛谷 | 计算机科学教育新生态
给定一个大小为 $n$ 的树,它共有 $n$ 个结点与 $n-1$ 条边,结点从 $1 \sim n$ 编号。初始时每个结点上都有一个 $1 \sim n$ 的数字,且每个 $1 \sim n$ 的数字都只在恰好一个结点上出现。
接下来你需要进行恰好 $n-1$ 次删边操作,每次操作你需要选一条未被删去的边,此时这条边所连接的两个结点上的数字将会交换,然后这条边将被删去。
$n-1$ 次操作过后,所有的边都将被删去。此时,按数字从小到大的顺序,将数字 $1 \sim n$ 所在的结点编号依次排列,就得到一个结点编号的排列 $P_i$ 。现在请你求出,在最优操作方案下能得到的字典序最小的 $P_i$ 。
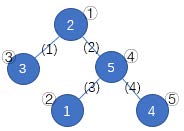
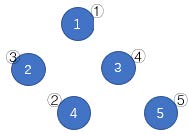
如上图,蓝圈中的数字 $1 \sim 5$ 一开始分别在结点②、①、③、⑤、④。按照 (1)(4)(3)(2) 的顺序删去所有边,树变为下图。按数字顺序得到的结点编号排列为①③④②⑤,该排列是所有可能的结果中字典序最小的。
一棵 $n$ 个节点的树上每个节点有一个 $1 \sim n$ 中的数字,定义对边 $(u, v)$ 进行删边操作为删边且交换 $u, v$ 节点上的数字,定义 $P_i$ 为数字 $i$ 所在的节点编号,求使得 $P_i$ 字典序最小的删边顺序。仅输出字典序最小的 $P_i$ 。
输入格式:
从文件 tree.in 中读入数据。
本题输入包含多组测试数据。
第一行一个正整数 $T$ ,表示数据组数。
对于每组测试数据:
第一行一个整数 $n$ ,表示树的大小。
第二行 $n$ 个整数,第 $i \ (1 \leq i \leq n)$ 个整数表示数字 $i$ 初始时所在的结点编号。
接下来 $n – 1$ 行每行两个整数 $x, y$ ,表示一条连接 $x$ 号结点与 $y$ 号结点的边。
输出格式:
输出到文件 tree.out 中。
对于每组测试数据,输出一行共 $n$ 个用空格隔开的整数,表示最优操作方案下所能得到的字典序最小的 $P_i$ 。
输入样例#1:
4 5 2 1 3 5 4 1 3 1 4 2 4 4 5 5 3 4 2 1 5 1 2 2 3 3 4 4 5 5 1 2 5 3 4 1 2 1 3 1 4 1 5 10 1 2 3 4 5 7 8 9 10 6 1 2 1 3 1 4 1 5 5 6 6 7 7 8 8 9 9 10
输出样例#1:
1 3 4 2 5 1 3 5 2 4 2 3 1 4 5 2 3 4 5 6 1 7 8 9 10
| 测试点编号 | $n \leq$ | 特殊性质 |
|---|---|---|
| $1 \sim 2$ | $10$ | 无 |
| $3 \sim 4$ | $160$ | 树的形态是一条链 |
| $5 \sim 7$ | $2000$ | 树的形态是一条链 |
| $8 \sim 9$ | $160$ | 存在度数为 $n-1$ 的结点 |
| $10 \sim 12$ | $2000$ | 存在度数为 $n-1$ 的结点 |
| $13 \sim 16$ | $160$ | 无 |
| $17 \sim 20$ | $2000$ | 无 |
由于作者水平有限,本题解表述、逻辑可能存在不足之处,欢迎读者以自身理解提出改进意见。
参考资料:[CSP-S2019]树上的数 – 仰望星空,脚踏实地 – 洛谷博客
刚看到这个题目的时候,总是想发掘树链上的性质,处理点上的信息,这种惯性思维使我完全没有思路。事实上,这个题处理边上的信息更好。
本题中,有 $25$ 分的菊花图部分分,在菊花图和链两个部分分中,菊花图事实上相对好思考一些,因此先考虑菊花图的情况。
假如我们已经得到了菊花图上删边的顺序为 $(1, u_1), (1, u_2), \dots, (1, u_m)$ ,则按顺序删边后,容易发现, $1$ 号点的数字移动至 $u_1$, $u_1$ 的数字移动至 $u_2$,……, $u_m$ 的数字移动至 $1$ 。
因此我们可以贪心地构造这个顺序,枚举数字 $1 \sim n$ ,每个数字贪心地选择删边顺序中的下一条边,该数字最后的位置就是该边对应的 $u_i$ 。
链的情况同样是 $25$ 分。
在链的情况中,分析边的关系是必要的。对于一个数字 $k$ 从初始位置 $u_1$ 移动至 $u_m$ ,在路径 $u_1, u_2, \dots, u_m$ 上有以下性质:
因此对于每个点可以获得一个删边的顺序,左先于右或右先于左。仍然按 $1 \sim n$ 的顺序枚举数字,检查每个数字从初始位置向左向右能走到的点中的最小编号。不能走仅当该点已确定的顺序不满足当前需要的顺序。
与链类似,对于一个数字 $k$ 从初始位置 $u_1$ 移动至 $u_m$ ,在路径 $u_1, u_2, \dots, u_m$ 上有以下性质:
容易发现,这些限制都是应用在某一点的边中的,因此可以单独考虑每个点的情况。依然是 $1 \sim n$ 枚举每个数字,从这个数字的初始位置开始 DFS ,检查路径上的点是否可以作为中间点/终点即可。
这里是这个题的实现中最难的位置,即检查是否满足中间点/终点的条件。这里,我使用了链表+并查集的实现方法管理边的关系。用类似链表的结构存储某个点的边是否被应用了在某边之后/之前被删的限制,用并查集存储某个点的边的限制连成的链式结构,且用两个数组 beg 和 end 存储某个点的边中,被固定为第一条/最后一条被删的边。
对于一个点,它能作为终点的条件为:
对于一个点,它能作为中间点的条件为:
根据以上条件进行判断一个点是否能作为中间点/终点,寻找每个数字的最小编号终点,并在路径上应用出入边的限制即可。
由于细节众多,文字描述无法包括所有方面,可以参考代码中的注释来理解。
UPD:被卡常了,开 O2 洛谷可过。
// Code by KSkun, 2019/11
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#include <vector>
#include <utility>
typedef long long LL;
typedef std::pair<int, int> PII;
inline char fgc() {
static char buf[100000], * p1 = buf, * p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
LL res = 0, neg = 1; char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
char c;
while(!isgraph(c = fgc())) {}
return c;
}
const int MAXN = 2005;
int T, n, ptn[MAXN], deg[MAXN], beg[MAXN], end[MAXN]; // 每个点的第一条/最后一条被删的边
std::vector<int> gra[MAXN];
struct UnionFindSet {
int fa[MAXN];
bool pre[MAXN], nxt[MAXN]; // 一条边有无前后关系
void clear() {
for (int i = 1; i <= n; i++) fa[i] = i;
memset(pre, 0, sizeof(pre));
memset(nxt, 0, sizeof(nxt));
}
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void join(int x, int y) {
int fx = find(x), fy = find(y);
fa[fy] = fx;
nxt[x] = pre[y] = true;
}
bool sameset(int x, int y) {
return find(x) == find(y);
}
} ufs[MAXN];
int dfs(int u, int f) {
int mn = n + 1;
// 能作为终点的条件:不是起点;入边可以是最后删边;入边之后无必须删边;入边和最后删边不在一条关系链中(只剩一条链时除外)
if (f != 0 && (end[u] == 0 || end[u] == f) && !ufs[u].nxt[f] &&
!(beg[u] != 0 && deg[u] > 1 && ufs[u].sameset(f, beg[u]))) {
mn = std::min(mn, u);
}
for (int v : gra[u]) {
if (v == f) continue;
if (f == 0) {
// 不能作为起点之后的点的条件:起点的最后删边不是这条;这条边之前有必须删的边;这条边与最后删边在同一条关系链中,且仍有未加入关系链中的边
if (beg[u] != 0 && beg[u] != v) continue;
if (ufs[u].pre[v]) continue;
if (end[u] != 0 && deg[u] > 1 && ufs[u].sameset(v, end[u])) continue;
mn = std::min(mn, dfs(v, u));
} else {
// 不能作为中间点的条件:入边是最后删边;出边是最先删边;入边和出边已在同一条关系链中;出边之前有必须删边;入边之后有必须删边;应用出入边关系后让最先删边和最后删边在同一条关系链中,且有其他边未在该关系链中
if (f == end[u] || v == beg[u] || ufs[u].sameset(f, v)) continue;
if (ufs[u].pre[v] || ufs[u].nxt[f]) continue;
if (beg[u] != 0 && end[u] != 0 && deg[u] > 2 &&
ufs[u].sameset(f, beg[u]) && ufs[u].sameset(v, end[u])) continue;
mn = std::min(mn, dfs(v, u));
}
}
return mn;
}
bool dfs2(int u, int f, int& tar) {
if (u == tar) {
end[u] = f; return true;
}
for (int v : gra[u]) {
if (v == f) continue;
if (dfs2(v, u, tar)) {
if (f == 0) {
beg[u] = v;
} else {
ufs[u].join(f, v);
deg[u]--;
}
return true;
}
}
return false;
}
int main() {
T = readint();
while (T--) {
n = readint();
// init
memset(beg, 0, sizeof(beg));
memset(end, 0, sizeof(end));
memset(deg, 0, sizeof(deg));
for (int i = 1; i <= n; i++) {
gra[i].clear();
ufs[i].clear();
}
// input
for (int i = 1; i <= n; i++) ptn[i] = readint();
for (int i = 1, x, y; i < n; i++) {
x = readint(); y = readint();
gra[x].push_back(y);
gra[y].push_back(x);
deg[x]++; deg[y]++; // deg 表示一个点的边关系构成的链的数量,初始为度数,之后每加入一个关系就对其减 1
}
// process
for (int i = 1; i <= n; i++) {
int mn = dfs(ptn[i], 0);
dfs2(ptn[i], 0, mn);
printf("%d ", mn);
}
putchar('\n');
}
return 0;
}题目地址:Codeforces:Problem – 5C – Codeforces、洛谷:CF5C Longest Regular Bracket Sequence – 洛谷 | 计算机科学教育新生态
This is yet another problem dealing with regular bracket sequences.
We should remind you that a bracket sequence is called regular, if by inserting «+» and «1» into it we can get a correct mathematical expression. For example, sequences «(())()», «()» and «(()(()))» are regular, while «)(», «(()» and «(()))(» are not.
You are given a string of «(» and «)» characters. You are to find its longest substring that is a regular bracket sequence. You are to find the number of such substrings as well.
给一个括号序列,求其最长的完全匹配连续子串长度及数量。
输入格式:
The first line of the input file contains a non-empty string, consisting of «(» and «)» characters. Its length does not exceed 10^6.
输出格式:
Print the length of the longest substring that is a regular bracket sequence, and the number of such substrings. If there are no such substrings, write the only line containing “0 1”.
输入样例#1:
)((())))(()())
输出样例#1:
6 2
输入样例#2:
))(
输出样例#2:
0 1
求括号序列匹配的常用方式是利用栈,即遇到一个左括号将其放入栈中,遇到一个右括号取栈顶元素并将这一对括号设置为已匹配。如果中间出现了未匹配段,则一定是右括号有多的,因此连续的已匹配段构成的子串一定是完全匹配子串。计算出匹配情况后,统计连续匹配的最长段及其数量即可。
// Code by KSkun, 2019/6
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <stack>
const int MAXN = 1000005;
int n;
bool match[MAXN];
char s[MAXN];
std::stack<int> sta;
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
for(int i = 1; i <= n; i++) {
if(s[i] == '(') sta.push(i);
else {
if(sta.empty()) continue;
int l = sta.top(); sta.pop();
match[l] = match[i] = true;
}
}
int mx = 0, mxcnt = 1, now = 0;
for(int i = 1; i <= n; i++) {
if(match[i]) {
now++;
} else {
if(now > mx) {
mx = now; mxcnt = 1;
} else if(now == mx) {
mxcnt++;
}
now = 0;
}
}
if(now > mx) {
mx = now; mxcnt = 1;
} else if(now == mx) {
mxcnt++;
}
if(mx == 0) mxcnt = 1;
printf("%d %d", mx, mxcnt);
return 0;
}
题目地址:洛谷:【P3957】跳房子 – 洛谷
跳房子,也叫跳飞机,是一种世界性的儿童游戏,也是中国民间传统的体育游戏之一。跳房子的游戏规则如下:
在地面上确定一个起点,然后在起点右侧画n个格子,这些格子都在同一条直线上。每个格子内有一个数字(整数),表示到达这个格子能得到的分数。玩家第一次从起点开始向右跳,跳到起点右侧的一个格子内。第二次再从当前位置继续向右跳,依此类推。规则规定:玩家每次都必须跳到当前位置右侧的一个格子内。玩家可以在任意时刻结束游戏,获得的分数为曾经到达过的格子中的数字之和。
现在小R研发了一款弹跳机器人来参加这个游戏。但是这个机器人有一个非常严重的缺陷,它每次向右弹跳的距离只能为固定的d。小R希望改进他的机器人,如果他花g个金币改进他的机器人,那么他的机器人灵活性就能增加g,但是需要注意的是,每次弹跳的距离至少为1。具体而言,当g<d时,他的机器人每次可以选择向右弹跳的距离为d-g,d-g+1,d-g+2,…,d+g-2,d+g-1,d+g;否则(当g≥d时),他的机器人每次可以选择向右弹跳的距离为1,2,3,…,d+g-2,d+g-1,d+g。
现在小R希望获得至少k分,请问他至少要花多少金币来改造他的机器人。
输入格式:
第一行三个正整数 n , d , k ,分别表示格子的数目,改进前机器人弹跳的固定距离,以及希望至少获得的分数。相邻两个数 之间用一个空格隔开。
接下来 n 行,每行两个正整数 xi, si ,分别表示起点到第 i 个格子的距离以及第 i 个格子的分数。两个数之间用一个空格隔开。保证 xi 按递增顺序输入。
输出格式:
共一行,一个整数,表示至少要花多少金币来改造他的机器人。若无论如何他都无法获得至少 k 分,输出 -1 。
输入样例#1:
7 4 10 2 6 5 -3 10 3 11 -3 13 1 17 6 20 2
输出样例#1:
2
输入样例#2:
7 4 20 2 6 5 -3 10 3 11 -3 13 1 17 6 20 2
输出样例#2:
-1

很容易看出来这应该是一个二分答案验证的套路,我们二分花费金币的数量,通过这个值确定跳跃的长度范围,可以用这样的DP来计算到每个位置为终点的最大路径和。
$$ dp[i] = \max_{\text{在跳跃范围内}} \{ dp[j] \} + val[i] $$
由于跳跃范围是定长区间,我们想到了滑动窗口,显然可以用单调队列来维护定长区间最大值,从而完成$O(1)$的转移。这样,复杂度就降为$O(n \log n)$,可以通过本题。
吐槽:好久没写代码了手都生成什么样子了QAQ,这破题还花了半小时……
// Code by KSkun, 2018/8
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
register char c;
while(!isgraph(c = fgc())) {}
return c;
}
const int MAXN = 5000005;
int n, d, k, dis[MAXN], val[MAXN], que[MAXN], ql, qr;
LL dp[MAXN], sum;
inline bool check(int mid) {
memset(dp, 0xc0, sizeof(dp));
dp[0] = 0;
int dl = std::max(1, d - mid), dr = d + mid, now = 0;
ql = qr = 0;
for(int i = 1; i <= n; i++) {
while(dis[i] - dis[now] >= dl && now < i) {
while(ql < qr && dp[que[qr - 1]] <= dp[now]) qr--;
que[qr++] = now; now++;
}
while(ql < qr && dis[i] - dis[que[ql]] > dr) ql++;
if(ql < qr) dp[i] = dp[que[ql]] + val[i];
if(dp[i] >= k) return true;
}
return false;
}
int main() {
n = readint(); d = readint(); k = readint();
for(int i = 1; i <= n; i++) {
dis[i] = readint(); val[i] = readint();
if(dis[i] > 0) sum += dis[i];
}
if(sum < k) {
puts("-1"); return 0;
}
int l = 0, r = dis[n] + 5, mid;
while(r - l > 1) {
mid = (l + r) >> 1;
if(check(mid)) r = mid; else l = mid;
}
printf("%d", r);
return 0;
}