题目地址：POJ：1151 — Atlantis、vjudge：Atlantis – POJ 1151 – Virtual Judge

题目描述

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
给若干矩形，求矩形并的总面积（即多个矩形重叠的部分只计算一次）。

输入输出格式

输入格式：
The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.
The input file is terminated by a line containing a single 0. Don’t process it.
输出格式：
For each test case, your program should output one section. The first line of each section must be Test case #k, where k is the number of the test case (starting with 1). The second one must be Total explored area: a, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.
Output a blank line after each test case.

输入输出样例

输入样例#1：

2
10 10 20 20
15 15 25 25.5
0

输出样例#1：

Test case #1
Total explored area: 180.00 

题解

本题是一个扫描线的经典应用，我们按x从小到大的顺序依次扫过矩形的每一条横边，统计每扫过这一段的覆盖宽度，计算出这一段的覆盖面积，加入答案。
具体而言，我们将y坐标离散化，这有利于用线段树存储y坐标。每扫到一个矩形的下边，就向线段树中插入这个下边线段，插入线段的权值是1；扫到一个上边，就插入权值为-1的线段。插入后，线段树动态维护当前覆盖的长度。当同一x坐标的线段都插入完成后，计算这一块的面积。
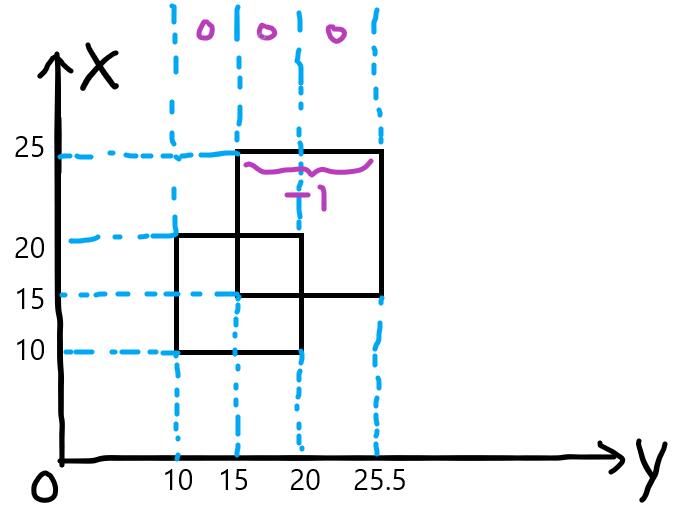
以样例为例吧。下图是样例的示意图。

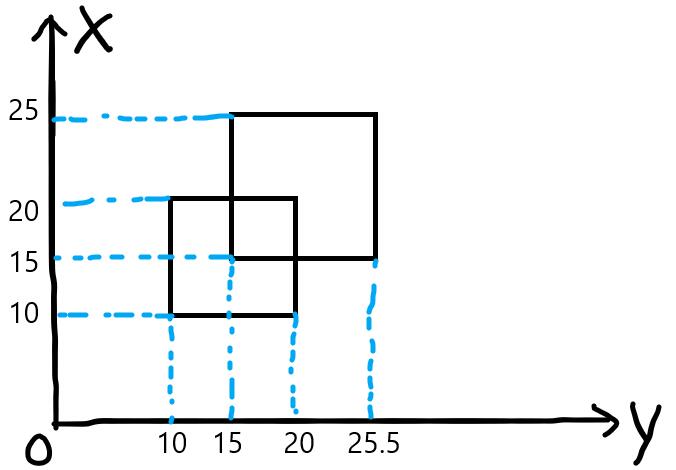
首先x=10的线段，向线段树中插入线段(10, 20)权值1，此时长度为10。

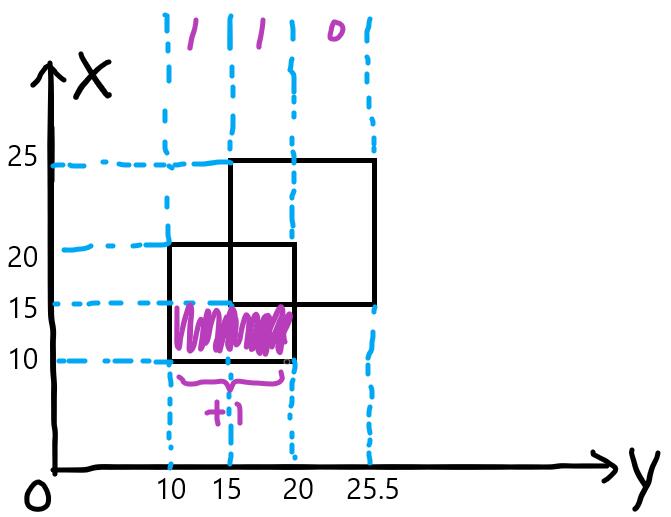
x=15的线段，向线段树中插入线段(15, 25.5)权值1，此时长度为20.5。

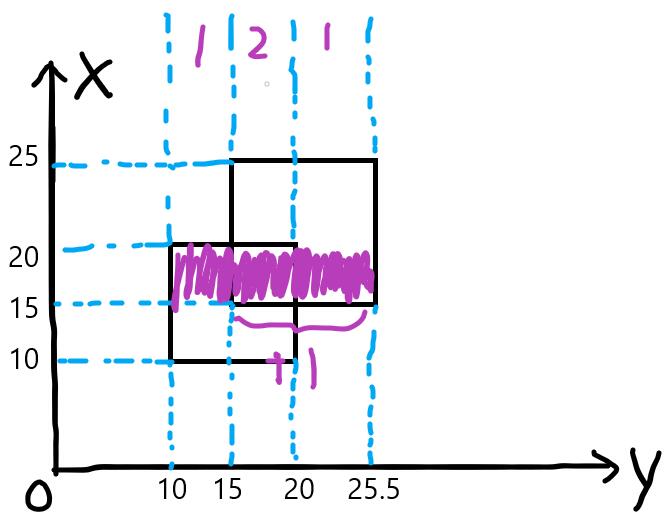
x=20的线段，向线段树中插入线段(10, 20)权值-1，此时长度为10.5。

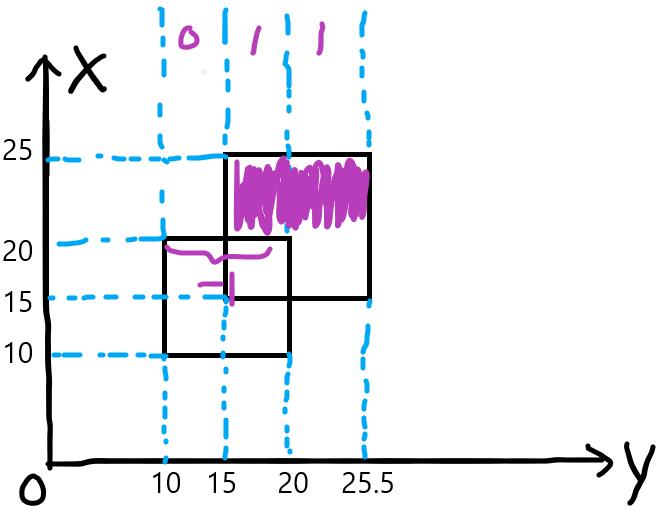
x=25的线段，向线段树中插入线段(15, 25.5)权值-1，此时长度为0。（其实这一步可以不做）

代码

// Code by KSkun. 2018/2
#include <cstdio> 
#include <cstring>
#include <vector>
#include <algorithm>

struct Line {
    double x, y1, y2;
    int v;
} line[205];

inline bool cmp(Line a, Line b) {
    return a.x < b.x; 
} 

int n, N, kase = 0;
double xa, ya, xb, yb, ans;
std::vector<double> vecy;
std::vector<double>::iterator yend;

// Segtree

#define lch o << 1
#define rch (o << 1) | 1
#define mid ((l + r) >> 1)

int val[1005];
double len[1005];

inline void callen(int o, int l, int r) {
    if(val[o] > 0) {
        len[o] = vecy[r - 1] - vecy[l - 1];
    } else {
        len[o] = len[lch] + len[rch];
    }
}

inline void add(int o, int l, int r, int ll, int rr, int v) {
    if(l == ll && r == rr) {
        val[o] += v;
        callen(o, l, r);
        return;
    }
    if(rr <= mid) {
        add(lch, l, mid, ll, rr, v);
    } else if(ll >= mid) {
        add(rch, mid , r, ll, rr, v);
    } else {
        add(lch, l, mid, ll, mid, v);
        add(rch, mid, r, mid, rr, v);
    }
    callen(o, l, r);
}

int main() {
    while(scanf("%d", &n) != EOF && n != 0) {
        kase++;
        ans = 0;
        vecy.clear();
        memset(val, 0, sizeof val);
        memset(len, 0, sizeof len);
        for(int i = 1; i <= n; i++) {
            scanf("%lf%lf%lf%lf", &xa, &ya, &xb, &yb);
            vecy.push_back(ya);
            vecy.push_back(yb);
            line[i].x = xa;
            line[i].y1 = ya;
            line[i].y2 = yb;
            line[i].v = 1;
            line[i + n].x = xb;
            line[i + n].y1 = ya;
            line[i + n].y2 = yb;
            line[i + n].v = -1;
        }
        std::sort(vecy.begin(), vecy.end());
        yend = std::unique(vecy.begin(), vecy.end());
        N = yend - vecy.begin();
        for(int i = 1; i <= n << 1; i++) {
            line[i].y1 = std::lower_bound(vecy.begin(), yend, line[i].y1) - vecy.begin() + 1;
            line[i].y2 = std::lower_bound(vecy.begin(), yend, line[i].y2) - vecy.begin() + 1;
        }
        std::sort(line + 1, line + (n << 1) + 1, cmp);
        add(1, 1, N, line[1].y1, line[1].y2, line[1].v);
        for(int i = 2; i <= n << 1; i++) {
            if(line[i].x > line[i - 1].x) {
                ans += len[1] * (line[i].x - line[i - 1].x);
            }
            add(1, 1, N, line[i].y1, line[i].y2, line[i].v);
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n", kase, ans);
    }
    return 0;
}