拉格朗日乘数法及其应用

概述
拉格朗日乘数法是数学中一种求带限制时多元函数的极值的常用方法。下面我们介绍拉格朗日乘数法的过程以及原理。
过程
对于多元函数f(x_1, x_2, \ldots, x_n),有限制g_1(x_1, x_2, \ldots, x_n)=0, \ldots, g_m(x_1, x_2, \ldots, x_n)=0,求原函数f的极值。
首先,我们对于每个限制引入拉格朗日乘数,分别为\lambda_1, \lambda_2, \ldots, \lambda_m,然后构造拉格朗日函数\mathcal{L}(x_1, x_2, \ldots, x_n, \lambda_1, \lambda_2, \ldots, \lambda_m) = f(x_1, x_2, \ldots, x_n) + \sum_{i=1}^m \lambda_ig_i(x_1, x_2, \ldots, x_n)。对于每一个未知数,对拉格朗日函数求偏导,得到方程组\frac{\partial \mathcal{L}}{\partial x_i} = 0及\frac{\partial \mathcal{L}}{\partial \lambda_i} = 0。该方程组的一个解即为原函数取得极值的一个解。
例子
问题:求双曲线xy = 3上离原点最近的点。
现在我们来求解它,首先问题可以转化为xy = 3时,f(x, y) = x^2 + y^2取得最小值的解。那么我们引入一个系数\lambda,构造拉格朗日函数为\mathcal{L}(x, y, \lambda) = x^2 + y^2 + \lambda(xy - 3)。对函数求偏导得到方程组如下:
\begin{cases} \frac{\partial \mathcal{L}}{\partial x} = 2x + \lambda y = 0 \\ \frac{\partial \mathcal{L}}{\partial y} = 2y + \lambda x = 0 \\ \frac{\partial \mathcal{L}}{\partial \lambda} = xy - 3 = 0 \end{cases}
解上面的方程组,得到一组解为
\begin{cases} \lambda = -2 \\ x = \sqrt{3} \\ y = \sqrt{3} \end{cases}
则点(\sqrt{3}, \sqrt{3})为一个所求点。
原理
注:下面的介绍仅提供一种理解方法,而非严谨证明。严谨证明参见:拉格朗日乘数 – 维基百科,自由的百科全书。
假如有函数f(x, y)及限制条件g(x, y) = c,我们可以类似地理上的等高线那样,在二维平面中绘制出f(x, y) = C的曲线,再把g(x, y) = c的曲线画上去。它可能看起来像下面这样。
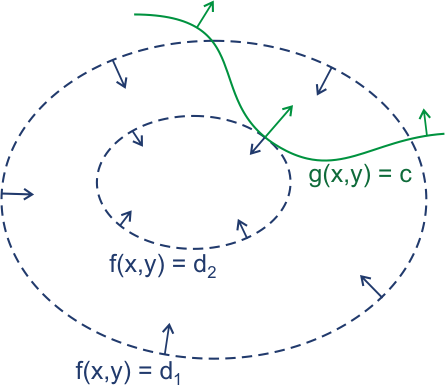
(图片来自维基百科:拉格朗日乘数 – 维基百科,自由的百科全书)
我们知道,f(x, y)的等高线和g(x, y) = c曲线的交点就是一组可行解。现在我们想求得极值,就要考虑上面的常数C取得极值时的情况,容易发现,当等高线与限制曲线相切的时候,就会出现极值。求出这个极值点的方法即为偏导取0时的解。

对函数求偏导得到方程组如下:
$$\begin{cases} \frac{\partial \mathcal{L}}{\partial x} = 2x – \lambda y = 0 \ \frac{\partial \mathcal{L}}{\partial y} = 2y – \lambda x = 0 \ \frac{\partial \mathcal{L}}{\partial \lambda} = xy – 3 = 0 \end{cases} $$
难道不应该是 $2x + \lambda y = 0$ ? 或者是我算错了?qwq
实在抱歉这个评论好像不滋磁latex qwq,我现在检查一下
是我打错了,抱歉qwq 已修正