[洛谷1357]花园 题解
题目地址:洛谷:【P1357】花园 – 洛谷 题目描述 小L有一座环形花园,沿 …
May all the beauty be blessed.
题目地址:洛谷:【P2331】[SCOI2005]最大子矩阵 – 洛谷、BZOJ:Problem 1084. — [SCOI2005]最大子矩阵
这里有一个n*m的矩阵,请你选出其中k个子矩阵,使得这个k个子矩阵分值之和最大。注意:选出的k个子矩阵不能相互重叠。
输入格式:
第一行为n,m,k(1≤n≤100,1≤m≤2,1≤k≤10),接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。
输出格式:
只有一行为k个子矩阵分值之和最大为多少。
输入样例#1:
3 2 2 1 -3 2 3 -2 3
输出样例#1:
9
我们注意到m的范围只有2,不如先想一下m=1的时候怎么做。我们可以设计一个状态dp[i][j]表示选到i这个位置且选择了j段的最大和。转移有两种情况,一是这个i位置不选进去,则从dp[i-1][j]转移过来;二是选进去,则枚举这个第j段的起点k,从dp[k-1][j-1]转移过来,加上这个第j段的和。
m=2的时候实际可以把上下两行拼一起做,因此矩形要么只有一行宽要么就是两行宽。设计状态dp[i][j][p]表示第一行到i位置,第二行到j位置,且分了p段的状态。i位置不选进去的情况变为2种,第一行不选进去和第二行不选进去,实际上第一第二都不选的情况已经包含进去了,可以从dp[i-1][j][p]和dp[i][j-1][p]转移过来。选进去的话,矩形全在第一行/全在第二行/两行都有三种情况都要枚举,即可以从dp[i][k][p-1]、dp[k][j][p-1]和dp[k][k][p-1]转移而来。
// Code by KSkun, 2018/4
#include <cstdio>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register char c = fgc(); register LL res = 0, neg = 1;
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 105;
int n, m, k, mat[MAXN][3], dp[MAXN][MAXN][15], sum[MAXN][3];
int main() {
n = readint(); m = readint(); k = readint();
for(int i = 1; i <= n; i++) {
sum[i][0] = sum[i - 1][0];
for(int j = 1; j <= m; j++) {
mat[i][j] = readint();
sum[i][j] = mat[i][j] + sum[i - 1][j];
sum[i][0] += mat[i][j];
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
for(int p = 1; p <= k; p++) {
dp[i][j][p] = std::max(dp[i][j - 1][p], dp[i - 1][j][p]);
for(int q = 1; q <= i; q++) {
dp[i][j][p] = std::max(dp[i][j][p],
dp[q - 1][j][p - 1] + sum[i][1] - sum[q - 1][1]);
}
for(int q = 1; q <= j; q++) {
dp[i][j][p] = std::max(dp[i][j][p],
dp[i][q - 1][p - 1] + sum[j][2] - sum[q - 1][2]);
}
for(int q = 1; q <= std::min(i, j); q++) {
dp[i][j][p] = std::max(dp[i][j][p],
dp[q - 1][q - 1][p - 1] + sum[std::min(i, j)][0] - sum[q - 1][0]);
}
}
}
}
printf("%d", dp[n][n][k]);
return 0;
}
965A Paper Airplanes 题意简述 一张纸可以做s个纸飞机,现在有k个人, …
题目地址:TopCoder Arena:Practice – TopCoder Arena、vjudge:CurvyonRails – TopCoder 12432 – Virtual Judge
There is a country with n cities, numbered 0 through n-1. City 0 is the capital. The road network in the country forms an undirected connected graph. In other words: Some pairs of cities are connected by bidirectional roads.
For every city there is at least one sequence of consecutive roads that leads from the city to the capital. (Whenever two roads need to cross outside of a city, the crossing is done using a bridge, so there are no intersections outside of the cities.)
You are given a linked that describes the road network. For each i and j, linked[i][j] is ‘Y’ if the cities i and j are already connected by a direct road, and it is ‘N’ otherwise.
The distance between two cities is the smallest number of roads one needs to travel to get from one city to the other. The people living outside of the capital are usually unhappy about their distance from the capital. You are also given a want with n elements. For each i, want[i] is the desired distance between city i and the capital (city 0).
Fox Ciel is in charge of building new roads. Each new road must again be bidirectional and connect two cities. Once the new roads are built, the citizens will evaluate how unhappy they are with the resulting road network:
For each i: Let real[i] be the new distance between city i and the capital. Then the people in city i increase the unhappiness of the country by (want[i] – real[i])^2.
Return the minimal total unhappiness Ciel can achieve by building some (possibly zero) new roads.
给定一个n个点的图,你现在可以往图上加边,每个点有个值want[i],加边后每个点到0的最短路为real[i],要求最小化\sum_{i=0}^{n-1} (want[i] - real[i])^2。
类名:FoxAndCity
函数名:minimalCost
参数:vector <string>, vector <int>
返回值:int
函数声明:int minimalCost(vector <string> linked, vector <int> want)
样例#1:
{"NYN", "YNY", "NYN"}
{0, 1, 1}
样例#1结果:
0
其他样例参见原网站。
参考资料:[最小割] SRM 590 div1 FoxAndCity – CSDN博客
我们考虑有以下性质:
因此我们可以建立最小割模型,类似[HNOI2013]切糕 题解 | KSkun’s Blog,对每个点的n-1种real[i]取值(0, 1, …, n-1)建点连成链,设置每个点对应的边的容量为选择该real[i]对答案的贡献,其中源→(i, real[i]=0)的点容量无限,因为要满足性质1。对于原图中有边相连的点(u, v),我们建边(u, real[u]=k)→(v, real[v]=k-1)表示性质2的限制。
注意0点的real只能取0,因此我们的源→(0, real[0]=0)边容量为0,可以选择不建。但是要建(0, real[0]=0)→T的边,容量无限,用于限制与0有边相连的点的real值。
由于TopCoder要求实现一个class,下面的代码并不是标准输入/输出格式(传统OI题目)的实现方式,但是把调试注释给去掉就可以用标准输入/输出了。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <queue>
const int MAXN = 1000005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
inline void reset() {
memset(head, -1, sizeof(head)); tot = 0;
}
int level[MAXN];
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == -1) {
level[v] = level[u] + 1;
if(v == t) return true;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || !left) return left;
int flow = 0;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
flow += d; left -= d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(!left) return flow;
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, S, T;
class FoxAndCity {
public:
inline int minimalCost(std::vector<std::string> linked, std::vector<int> want) {
n = linked.size();
S = n * n + 1; T = S + 1;
reset();
addedge(1, T, INF);
for(int i = 2; i <= n; i++) {
addedge(S, (i - 1) * n + 1, INF);
for(int j = 1; j < n; j++) {
addedge((i - 1) * n + j, (i - 1) * n + j + 1,
(j - want[i - 1]) * (j - want[i - 1]));
}
addedge((i - 1) * n + n, T, INF);
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(linked[i - 1][j - 1] == 'Y') {
for(int k = 1; k < n; k++) {
addedge((i - 1) * n + k + 1, (j - 1) * n + k, INF);
}
}
}
}
return dinic(S, T);
}
};
/*int main() {
FoxAndCity solver;
printf("%d", solver.minimalCost({"NYNNNY", "YNYNNN", "NYNYNN", "NNYNYN",
"NNNYNY", "YNNNYN"}, {0, 2, 2, 2, 2, 2}));
return 0;
}*/
题目地址:洛谷:【P3965】[TJOI2013]循环格 – 洛谷、BZOJ:Problem 3171. — [Tjoi2013]循环格
一个循环格就是一个矩阵,其中所有元素为箭头,指向相邻四个格子。每个元素有一个坐标(行,列),其中左上角元素坐标为(0,0)。给定一个起始位(r,c),你可以沿着箭头方向在格子间行走。即:如果(r,c)是一个左箭头,那么走到(r,c-1);如果是一个右箭头,走到(r,c+1);如果是上箭头,走到(r-1,c);如果是下箭头,走到(r+1,c)。每一行和每一列都是循环的,即如果走出边界,你会出现在另一侧。比如在一个5*5的循环格里,从(3,0)向左走会出现在(3,4)。
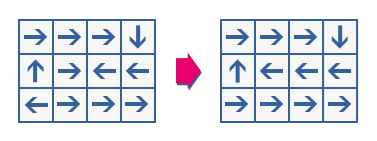
一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。例如下图,左边不是一个完美的循环格,因为只有从(1,1),(1,2),(2,0),(2,3)出发才会回到起始位置。通过修改其中两个箭头,可以得到右图,一个完美的循环格。
给定一个循环格,你需要计算最少需要修改多少个元素使其完美。
输入格式:
第一行两个整数R和C,表示循环格的行和列。接下来R行,每一行包含C个字符LRUD表示左右上下
输出格式:
一个整数,表示最少需要修改多少个元素使得给定的循环格完美。
输入样例#1:
4 4 RRRD URDD UULD ULLL
输出样例#1:
0
输入样例#2:
3 4 RRRD URLL LRRR
输出样例#2:
2
数据范围
30%的数据,1 ≤ R, C ≤ 7
100%的数据,1 ≤ R, C ≤ 15
把方格图抽象成图,我们得出结论:一个循环上的点,入度=出度=1。而题目则让我们求一个使原图变为由多个环组成的图的最小费用。如果我们对于每个点拆点,分别表示入度和出度,则本题就是一个流量平衡问题,即流入=流出=1。
我们将原图中的每一条已经存在的边的出点出度点与入点入度点相连,这样就完成了一个二分图。如果该二分图存在完全匹配(或者说,可以跑满流),则说明这个图本来就是合法的,不需要对边进行改动。如果需要改动边,我们考虑改成一个费用流的网络,对于不存在的边,建成容量1费用1的边即可。接着就是对这个二分图求最小权匹配的事情,可以用费用流来解决。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline bool isdir(char c) {
return c == 'R' || c == 'L' || c == 'U' || c == 'D';
}
inline char readdir() {
char c;
while(!isdir(c = fgc()));
return c;
}
const int MAXN = 100005, INF = 1e9;
struct Edge {
int to, cap, cost, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap, int cost) {
gra[tot] = Edge {v, cap, cost, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, -cost, head[v]}; head[v] = tot++;
}
int f[MAXN], dis[MAXN], pre[MAXN], pree[MAXN];
std::queue<int> que;
bool inque[MAXN];
inline bool spfa(int s, int t) {
memset(f, 0, sizeof(f));
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; inque[s] = true; f[s] = INF; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop(); inque[u] = false;
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && dis[v] > dis[u] + gra[i].cost) {
pre[v] = u; pree[v] = i;
f[v] = std::min(f[u], gra[i].cap);
dis[v] = dis[u] + gra[i].cost;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
return f[t];
}
int flow, cost;
inline void mcmf(int s, int t) {
while(spfa(s, t)) {
for(int i = t; i != s; i = pre[i]) {
gra[pree[i]].cap -= f[t];
gra[pree[i] ^ 1].cap += f[t];
}
flow += f[t];
cost += f[t] * dis[t];
}
}
const int fix[2][4] = {{1, -1, 0, 0}, {0, 0, 1, -1}};
const char dirs[] = {'D', 'U', 'R', 'L'};
int n, m, S, T;
char dir;
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint();
S = n * m * 2 + 1; T = S + 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
dir = readdir();
addedge(S, (i - 1) * m + j, 1, 0);
addedge((i - 1) * m + j + n * m, T, 1, 0);
for(int k = 0; k < 4; k++) {
int nx = i + fix[0][k], ny = j + fix[1][k];
if(nx == 0) nx = n; if(nx == n + 1) nx = 1;
if(ny == 0) ny = m; if(ny == m + 1) ny = 1;
addedge((i - 1) * m + j, (nx - 1) * m + ny + n * m, 1, dir != dirs[k]);
}
}
}
mcmf(S, T);
printf("%d", cost);
return 0;
}