[BJOI2006]狼抓兔子 题解
![[BJOI2006]狼抓兔子 题解](https://ksmeow.moe/wp-content/uploads/2018/04/180420a.jpg "180420a")
题目地址：洛谷：【P4001】[BJOI2006]狼抓兔子 – 洛谷、BZOJ：Problem 1001. — [BeiJing2006]狼抓兔子
题目描述
现在小朋友们最喜欢的”喜羊羊与灰太狼”,话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：
![catch bjoi06 - [BJOI2006]狼抓兔子 题解](https://ksmeow.moe/wp-content/uploads/2018/04/catch_bjoi06.png "[BJOI2006]狼抓兔子 题解")
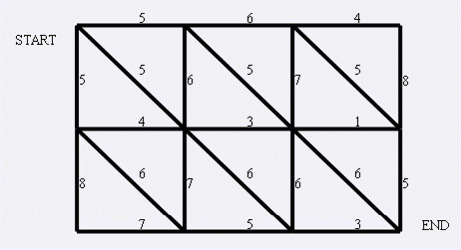
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
输入输出格式
输入格式：
第一行为N,M.表示网格的大小，N,M均小于等于1000.
接下来分三部分
第一部分共N行，每行M-1个数，表示横向道路的权值.
第二部分共N-1行，每行M个数，表示纵向道路的权值.
第三部分共N-1行，每行M-1个数，表示斜向道路的权值.
输出格式：
输出一个整数，表示参与伏击的狼的最小数量.
输入输出样例
输入样例#1：
3 4 5 6 4 4 3 1 7 5 3 5 6 7 8 8 7 6 5 5 5 5 6 6 6
输出样例#1：
14
题解
网络流
我们可以直接按照图示建立网络，求最小割。Dinic跑是很快的。
对偶图
这有个讲解对偶图的ppt：点击下载
然后我们可以利用对偶图的性质，建立对偶图，求S到T的最短路，即为最小割。这样来做点数边数能够变小，避免了空间爆炸的情况。
下面的代码中，建图的规律是第一行右上三角形的编号为1~m-1，左下三角形的编号为m~2m-2，底下以此类推。需要判断越界的面属于S还是T。
代码
网络流
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 2000005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXN * 5];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, cap, head[v]}; head[v] = tot++;
}
int level[MAXN];
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(level[v] == -1 && gra[i].cap > 0) {
level[v] = level[u] + 1;
if(v == t) return true;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || left <= 0) return left;
int flow = 0;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
flow += d; left -= d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(left <= 0) break;
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, m, t;
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint();
for(int i = 1; i <= n; i++) {
for(int j = 1; j < m; j++) {
t = readint();
addedge((i - 1) * m + j, (i - 1) * m + j + 1, t);
}
}
for(int i = 1; i < n; i++) {
for(int j = 1; j <= m; j++) {
t = readint();
addedge((i - 1) * m + j, i * m + j, t);
}
}
for(int i = 1; i < n; i++) {
for(int j = 1; j < m; j++) {
t = readint();
addedge((i - 1) * m + j, i * m + j + 1, t);
}
}
printf("%d", dinic(1, n * m));
return 0;
}
对偶图
参考资料：【BJOI2006】狼抓兔子 – flow丶 – 博客园
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 2000005, INF = 1e9;
struct Edge {
int to, w, nxt;
} gra[MAXN << 2];
int head[MAXN], tot;
inline void addedge(int u, int v, int w) {
gra[tot] = Edge {v, w, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, w, head[v]}; head[v] = tot++;
}
int dis[MAXN];
bool inque[MAXN];
inline void spfa(int s) {
std::queue<int> que;
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; inque[s] = true;
que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop(); inque[u] = false;
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(dis[v] > dis[u] + gra[i].w) {
dis[v] = dis[u] + gra[i].w;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
}
int n, m, t, S, T;
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint();
S = 0; T = (n - 1) * (m - 1) * 2 + 1;
int u = 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j < m; j++) {
t = readint();
int v = u - (m - 1), u1 = u, v1 = v;
if(v <= S) v1 = S;
if(u >= T) u1 = T;
addedge(u1, v1, t);
u++;
}
u += m - 1;
}
u = m;
for(int i = 1; i < n; i++) {
for(int j = 1; j <= m; j++) {
t = readint();
int v = u - m, u1 = u, v1 = v;
if(v <= 2 * (i - 1) * (m - 1)) v1 = T;
if(u > 2 * i * (m - 1)) u1 = S;
addedge(u1, v1, t);
u++;
}
u += m - 2;
}
u = 1;
for(int i = 1; i < n; i++) {
for(int j = 1; j < m; j++) {
t = readint();
addedge(u, u + m - 1, t);
u++;
}
u += m - 1;
}
spfa(S);
printf("%d", dis[T]);
return 0;
}
