Codeforces Round #462 (Div. 2) 题解

比赛地址:Dashboard – Codeforces Round #462 (Div. 2) – Codeforces,也可以在底下的赛题列表点进题目。
赛题列表
#A 934A – A Compatible Pair | 暴力,枚举
#B 934B – A Prosperous Lot | 贪心
#C 933A – A Twisty Movement | 枚举
#D 933B – A Determined Cleanup | 数学
#E 933C – A Colourful Prospect | 计算几何
934A A Compatible Pair
题目描述
给两个数列a, b长分别为n, m,其中a数列要删去一个数,求一种删数的方案,使得所有a_i \cdot b_j中的最大值最小。只需要输出这个最小值。
数据范围:2 \leq n, m \leq 50
样例
样例1
输入:
2 2 20 18 2 14
输出:
252
说明:
删去20,此时最大值为18*14=252。
样例2
输入:
5 3 -1 0 1 2 3 -1 0 1
输出:
2
说明:
删去3,最大值为2*1=2。
题解
枚举删去的数,然后枚举求出此时最大值,维护全部情况的最大值的最小值即可。
复杂度:O(n^3)
代码
// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>
int n, m;
long long ans = 1e18 + 10;
long long a[55], b[55];
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
}
for(int i = 1; i <= m; i++) {
scanf("%lld", &b[i]);
}
for(int k = 1; k <= n; k++) {
long long mx = -1e18 - 10;
for(int i = 1; i <= n; i++) {
if(i == k) continue;
for(int j = 1; j <= m; j++) {
mx = std::max(mx, a[i] * b[j]);
}
}
ans = std::min(ans, mx);
}
printf("%lld", ans);
return 0;
}
934B A Prosperous Lot
题目描述
定义一个数的圈的个数为这个数中包含数码的圈的个数和,其中,数码的圈的个数依照下图计算。
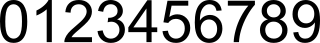
例如,8的圈的个数为2,而5的圈的个数为0。
给定一个数k,求任意一个不大于10^{18}的非负整数使得其圈的个数为k。如果不存在,输出-1。
数据范围:1 \leq k \leq 10^6
样例
样例1
输入:
2
输出:
462
样例2
输入:
6
输出:
8080
题解
我们知道8有两个圈,而6有一个圈。先贪心一下,全用8,如果还剩下1就用1个6,加一起长度超没超18。超了就无解,没超就输出。
复杂度:O(1)
代码
// Code by KSkun, 2018/2
#include <cstdio>
int k, c2, c1;
int main() {
scanf("%d", &k);
c2 = k / 2;
c1 = k % 2;
if(c1 + c2 > 18) {
printf("-1");
return 0;
}
if(c1) putchar('6');
for(int i = 1; i <= c2; i++) putchar('8');
return 0;
}
933A A Twisty Movement
题目描述
给定一个只由1和2构成的数列,长为n,有一次机会翻转任意区间[l, r],求一种翻转方法,使得翻转后的序列的LIS最长。只需要输出最长的LIS长度。
数据范围:1 \leq n \leq 2000
样例
样例1
输入:
4 1 2 1 2
输出:
4
说明:
翻转区间[2, 3]得到序列1 1 2 2。
样例2
输入:
10 1 1 2 2 2 1 1 2 2 1
输出:
9
说明:翻转区间[3, 7]得到序列1 1 1 1 2 2 2 2 2 1。
题解
这个题需要一些思考。
首先传统的LIS求法是O(n \log n)的,但是12序列可以做到O(n)的。枚举LIS中1和2的分界点,即为该点前1的个数加该点后2的个数。可以分别预处理出来。
我们考虑枚举分界点,然后枚举翻转的区间。可以发现,如果分界点不在区间内部,翻转区间是没有用的。所以区间应该包含这个分界点。翻转后的答案应该是1~区间左端点1的个数+区间左端点~分界点2的个数+分界点~区间右端点1的个数+区间右端点~n 2的个数。左端点和右端点的计算是分开的,所以可以分开枚举分别求最大值,加起来就是一个完整的最大值。
复杂度:O(n^2)
代码
// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>
int n, a[2005], c1[2005], c2[2005], ans = 0;
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
c1[i] = c1[i - 1];
c2[i] = c2[i - 1];
if(a[i] == 1) {
c1[i]++;
} else {
c2[i]++;
}
}
for(int i = 0; i <= n; i++) {
ans = std::max(ans, c1[i] + c2[n] - c2[i]);
}
for(int i = 0; i <= n; i++) {
int mx1 = 0, mx2 = 0;
for(int l = 1; l < i; l++) {
mx1 = std::max(mx1, c1[l - 1] + c2[i - 1] - c2[l - 1]);
}
for(int r = i; r <= n; r++) {
mx2 = std::max(mx2, c1[r] - c1[i - 1] + c2[n] - c2[r]);
}
ans = std::max(ans, mx1 + mx2);
}
printf("%d", ans);
return 0;
}
933B A Determined Cleanup
题目描述
给两个数p和k,要求求一个多项式f(x),使得f(x)满足f(x)=q(x) \cdot (x+k)+p,其中q(x)是另一个多项式,且f(x)各项的系数和常数项都不大于k。如果无解,输出-1。
数据范围:1 \leq p \leq 10^{18}, 2 \leq k \leq 2000
样例
样例1
输入:
46 2
输出:
7 0 1 0 0 1 1 1
说明:
f(x) = x^6 + x^5 + x^4 + x = (x^5 - x^4 + 3x^3 - 6x^2 + 12x - 23)(x + 2) + 46
样例2
输入:
2018 214
输出:
3 92 205 1
说明:
f(x) = x^2 + 205x + 92 = (x - 9)(x + 214) + 2018
题解
本题需要用到余式定理。余式定理的内容是多项式f(x)除以多项式(x – a)的余式为f(a)。
余式定理的证明可以参考余式定理_百度百科。
这里需要f(x)除以(x + k)余p,就是说f(-k) = p。那么我们只需要将p化成一个-k进制数即可。这样看来,本题不存在无解的情况。
复杂度:O(\log p)
代码
// Code by KSkun, 2018/2
#include <cstdio>
#include <vector>
long long p;
int k;
std::vector<int> vec;
int main() {
scanf("%lld%d", &p, &k);
while(p != 0) {
vec.push_back((p % k + k) % k);
p = (vec.back() - p) / k;
}
printf("%d\n", vec.size());
for(int i = 0; i < vec.size(); i++) {
printf("%d ", vec[i]);
}
return 0;
}
933C A Colourful Prospect
题目描述
给n个圆,求n个圆将平面分成几个区域(内部不包含任何弧线)。
数据范围:1 \leq n \leq 3
样例
样例1
输入:
3 0 0 1 2 0 1 4 0 1
输出:
4
说明:
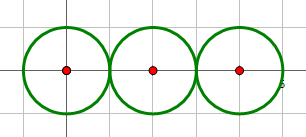
样例2
输入:
3 0 0 2 3 0 2 6 0 2
输出:
6
说明:
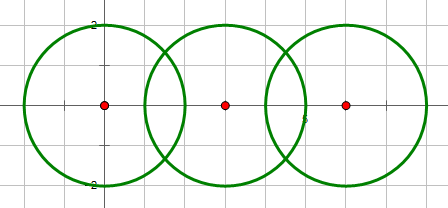
样例3
输入:
3 0 0 2 2 0 2 1 1 2
输出:
8
说明:
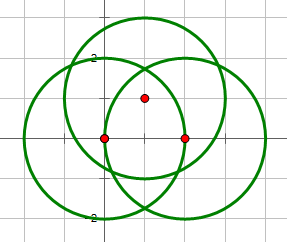
题解
需要使用欧拉定理(V-E+F=2)解决。暂未解决。
复杂度:
