题目地址：洛谷：【P1169】[ZJOI2007]棋盘制作 – 洛谷、BZOJ：Problem 1057. — [ZJOI2007]棋盘制作

题目描述

国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想，棋盘是一个8*8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。
而我们的主人公小Q，正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由N*M个正方形的格子组成的矩形纸片，每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘，当然，他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘（当然，不管哪种，棋盘必须都黑白相间，即相邻的格子不同色），所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积，从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你，你能帮助他么？

输入输出格式

输入格式：
包含两个整数N和M，分别表示矩形纸片的长和宽。接下来的N行包含一个N * M的01矩阵，表示这张矩形纸片的颜色（0表示白色，1表示黑色）。
输出格式：
包含两行，每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积，第二行为可以找到的最大矩形棋盘的面积（注意正方形和矩形是可以相交或者包含的）。

输入输出样例

输入样例#1：

3 3
1 0 1
0 1 0
1 0 0

输出样例#1：

4
6

说明

对于20%的数据，N, M ≤ 80
对于40%的数据，N, M ≤ 400
对于100%的数据，N, M ≤ 2000

题解

这道题是一个最大子矩形（考虑障碍点，点无权值）的模型，可以采用悬线法解决。关于悬线法，这里将会详细介绍。

将黑白交替统一化

通过思考，发现棋盘只有2种，一是两坐标奇偶相同时白，二是不同时白。为了统一黑白交替的情况，我们可以将同一种棋盘的一部分用一个记号表示。比如将两坐标奇偶相同的白格子和两坐标奇偶不同的黑格子记为1，另一种情况以此类推。这样就成了最大全0/全1矩阵问题了。

朴素的悬线法

首先我们给定悬线的定义：以一个点为终点的悬线是一条竖直的以上边界或最近障碍点为起点的线段。如下图，黑色为边界，紫色点为障碍点，蓝色为悬线，红色不是悬线。

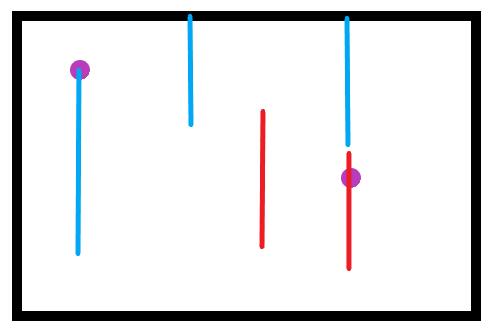
如果一个悬线左右平移，即可扫出一个矩形，也就是说，对于每个点，我们只需要求出它的悬线长与左右最多能平移的距离。下面我们用h[i][j]表示点(i, j)处的悬线长，l[i][j]表示向左最多能平移到的位置，r[i][j]表示向右最多能平移到的位置。如图，紫色为蓝色悬线能扫过的最大矩形。

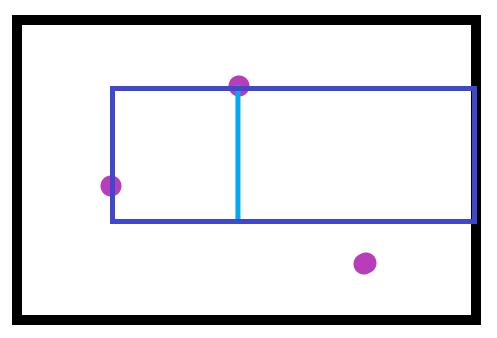
对于i=1的一排点，h值显然为0。对于j=1的一列点，l值显然为1。对于j=m的一列点，r值显然为m。除此以外，任何点的h值应该不大于n，l值应该不小于1，r值应该不大于n。
考虑每一个数组如何递推得到它的值。各位可以以下图作为参考。

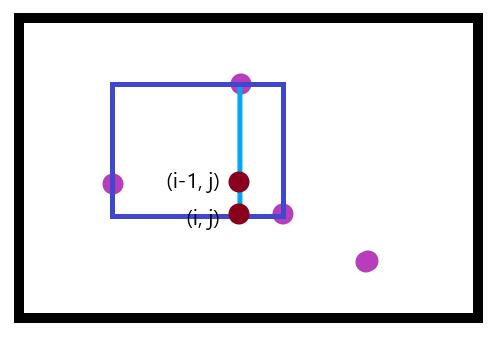
对于h数组，如果该点为上边界点或障碍点，h值为0。否则有h[i][j]=h[i-1][j]+1。
对于l数组，考虑这个点左边最近的障碍点/边界点，令这个点的位置为L。有l[i][j]=max(l[i-1][j], L)。
同理有r[i][j]=min(r[i-1][j], R)。
这样我们就得到了这三个数组的递推式。需要注意的是，l数组从左向右更新，而r数组从右向左。

优化空间：滚动数组

发现i层只跟i-1层有关系，自然可以滚动。

优化空间：降维

发现转移只跟j相同的状态有关，i维度可以删去。

正方形？

正方形一定在极大子矩形中，通过极大子矩形的短边长计算即可。

复杂度

代码

// Code by KSkun. 2018/2
#include <cstdio>
#include <cstring>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

int n, m, l[2005], r[2005], x[2005], L, R, ans1 = 0, ans2 = 0, sedge;
bool mmp[2005][2005];

inline void workdp() {
    memset(x, 0, sizeof x);
    for(int i = 1; i <= m; i++) {
        l[i] = 1;
        r[i] = m;
    }
    for(int i = 1; i <= n; i++) {
        L = 0;
        R = m + 1;
        for(int j = 1; j <= m; j++) {
            if(mmp[i][j]) {
                l[j] = 1;
                L = j;
                x[j] = 0;
            } else {
                x[j]++;
                l[j] = std::max(l[j], L + 1);
            }
        } 
        for(int j = m; j >= 1; j--) {
            if(mmp[i][j]) {
                r[j] = m;
                R = j;
            } else {
                r[j] = std::min(r[j], R - 1);
            }
            sedge = std::min(x[j], r[j] - l[j] + 1);
            ans1 = std::max(ans1, sedge * sedge); // 正方形
            ans2 = std::max(ans2, x[j] * (r[j] - l[j] + 1)); // 矩形 
        }
    }
}

int main() {
    n = read();
    m = read();
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            mmp[i][j] = read();
            if((i & 1) == (j & 1)) {
                mmp[i][j] = !mmp[i][j];
            }
        }
    }
    workdp();
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            mmp[i][j] = !mmp[i][j];
        }
    } 
    workdp();
    printf("%d\n%d", ans1, ans2);
    return 0;
}

变式

点上有权值，求最大权子矩形

预处理二维前缀和，计算极大子矩形的时候用前缀和即可

另外一种做法

计算出每个点向左向右值相同的个数，对每一列上的每个点求上下不小于该点值的最长长度，乘上该点值即为这个点所在的极大子矩形面积。