题目地址：洛谷：【P3965】[TJOI2013]循环格 – 洛谷、BZOJ：Problem 3171. — [Tjoi2013]循环格

题目描述

一个循环格就是一个矩阵,其中所有元素为箭头,指向相邻四个格子。每个元素有一个坐标(行,列),其中左上角元素坐标为(0,0)。给定一个起始位(r,c),你可以沿着箭头方向在格子间行走。即:如果(r,c)是一个左箭头，那么走到(r,c-1);如果是一个右箭头,走到(r,c+1);如果是上箭头,走到(r-1,c);如果是下箭头,走到(r+1,c)。每一行和每一列都是循环的,即如果走出边界,你会出现在另一侧。比如在一个5*5的循环格里,从(3,0)向左走会出现在(3,4)。

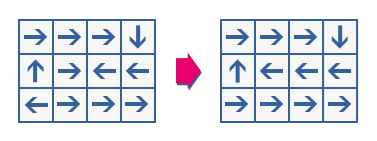
一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。例如下图,左边不是一个完美的循环格,因为只有从(1,1),(1,2),(2,0),(2,3)出发才会回到起始位置。通过修改其中两个箭头,可以得到右图,一个完美的循环格。
给定一个循环格,你需要计算最少需要修改多少个元素使其完美。

输入输出格式

输入格式：
第一行两个整数R和C,表示循环格的行和列。接下来R行,每一行包含C个字符LRUD表示左右上下

输出格式：
一个整数,表示最少需要修改多少个元素使得给定的循环格完美。

输入输出样例

输入样例#1：

4 4
RRRD
URDD
UULD
ULLL

输出样例#1：

0

输入样例#2：

3 4
RRRD
URLL
LRRR

输出样例#2：

2

说明

数据范围
30%的数据，1 ≤ R, C ≤ 7
100%的数据，1 ≤ R, C ≤ 15

题解

把方格图抽象成图，我们得出结论：一个循环上的点，入度=出度=1。而题目则让我们求一个使原图变为由多个环组成的图的最小费用。如果我们对于每个点拆点，分别表示入度和出度，则本题就是一个流量平衡问题，即流入=流出=1。
我们将原图中的每一条已经存在的边的出点出度点与入点入度点相连，这样就完成了一个二分图。如果该二分图存在完全匹配（或者说，可以跑满流），则说明这个图本来就是合法的，不需要对边进行改动。如果需要改动边，我们考虑改成一个费用流的网络，对于不存在的边，建成容量1费用1的边即可。接着就是对这个二分图求最小权匹配的事情，可以用费用流来解决。

代码

// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>

#include <queue>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF 
        : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    register char c = fgc();
    while(c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

inline bool isdir(char c) {
    return c == 'R' || c == 'L' || c == 'U' || c == 'D';
}

inline char readdir() {
    char c;
    while(!isdir(c = fgc()));
    return c;
}

const int MAXN = 100005, INF = 1e9;

struct Edge {
    int to, cap, cost, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;

inline void addedge(int u, int v, int cap, int cost) {
    gra[tot] = Edge {v, cap, cost, head[u]}; head[u] = tot++;
    gra[tot] = Edge {u, 0, -cost, head[v]}; head[v] = tot++;
}

int f[MAXN], dis[MAXN], pre[MAXN], pree[MAXN];
std::queue<int> que;
bool inque[MAXN];

inline bool spfa(int s, int t) {
    memset(f, 0, sizeof(f));
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0; inque[s] = true; f[s] = INF; que.push(s);
    while(!que.empty()) {
        int u = que.front(); que.pop(); inque[u] = false;
        for(int i = head[u]; ~i; i = gra[i].nxt) {
            int v = gra[i].to;
            if(gra[i].cap > 0 && dis[v] > dis[u] + gra[i].cost) {
                pre[v] = u; pree[v] = i;
                f[v] = std::min(f[u], gra[i].cap);
                dis[v] = dis[u] + gra[i].cost;
                if(!inque[v]) {
                    inque[v] = true;
                    que.push(v);
                }
            }
        }
    }
    return f[t];
}

int flow, cost;

inline void mcmf(int s, int t) {
    while(spfa(s, t)) {
        for(int i = t; i != s; i = pre[i]) {
            gra[pree[i]].cap -= f[t];
            gra[pree[i] ^ 1].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

const int fix[2][4] = {{1, -1, 0, 0}, {0, 0, 1, -1}};
const char dirs[] = {'D', 'U', 'R', 'L'};

int n, m, S, T;
char dir;

int main() {
    memset(head, -1, sizeof(head));
    n = readint(); m = readint();
    S = n * m * 2 + 1; T = S + 1;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            dir = readdir();
            addedge(S, (i - 1) * m + j, 1, 0);
            addedge((i - 1) * m + j + n * m, T, 1, 0);
            for(int k = 0; k < 4; k++) {
                int nx = i + fix[0][k], ny = j + fix[1][k];
                if(nx == 0) nx = n; if(nx == n + 1) nx = 1;
                if(ny == 0) ny = m; if(ny == m + 1) ny = 1;
                addedge((i - 1) * m + j, (nx - 1) * m + ny + n * m, 1, dir != dirs[k]);
            }
        }
    }
    mcmf(S, T);
    printf("%d", cost);
    return 0;
}