[JSOI2008]Blue Mary开公司 题解
![[JSOI2008]Blue Mary开公司 题解](https://ksmeow.moe/wp-content/uploads/2018/02/180225a.png)
题目地址:洛谷:、BZOJ:Problem 1568. — [JSOI2008]Blue Mary开公司
题目背景
Blue Mary 最近在筹备开一家自己的网络公司。由于他缺乏经济头脑,所以先后聘请了若干个金融顾问为他设计经营方案。
题目描述
万事开头难,经营公司更是如此。开始的收益往往是很低的,不过随着时间的增长会慢慢变好。也就是说,对于一个金融顾问 i,他设计的经营方案中,每天的收益都比前一天高,并且均增长一个相同的量 Pi。
由于金融顾问的工作效率不高,所以在特定的时间,Blue Mary 只能根据他已经得到的经营方案来估算某一时间的最大收益。由于 Blue Mary 是很没有经济头脑的,所以他在估算每天的最佳获益时完全不会考虑之前的情况,而是直接从所有金融顾问的方案中选择一个在当天获益最大的方案的当天的获益值,例如:
有如下两个金融顾问分别对前四天的收益方案做了设计:
| 第一天 | 第二天 | 第三天 | 第四天 | Pi | |
|---|---|---|---|---|---|
| 顾问 1 | 1 | 5 | 9 | 13 | 4 |
| 顾问 2 | 2 | 5 | 8 | 11 | 3 |
在第一天,Blue Mary认为最大收益是 2(使用顾问 2 的方案),而在第三天和第四天,他认为最大收益分别是 9 和 13(使用顾问 1 的方案)。而他认为前四天的最大收益是:
2 + 5 + 9 + 13 = 29
现在你作为 Blue Mary 公司的副总经理,会不时收到金融顾问的设计方案,也需要随时回答 Blue Mary 对某天的“最大收益”的询问(这里的“最大收益”是按照 Blue Mary 的计算方法)。一开始没有收到任何方案时,你可以认为每天的最大收益值是 0。下面是一组收到方案和回答询问的例子:
询问 2 回答 0 收到方案:0 1 2 3 4 5 …… 询问 2 回答 1 收到方案:2 2.1 2.2 2.3 2.4 …… 询问 2 回答 2.1
输入输出格式
输入格式:
第一行 :一个整数 N,表示方案和询问的总数。
接下来 N 行,每行开头一个单词Query或Project。
若单词为Query,则后接一个整数 T,表示 Blue Mary 询问第 T 天的最大收益。
若单词为Project,则后接两个实数 S,P,表示该种设计方案第一天的收益 S,以及以后每天比上一天多出的收益 P。
输出格式:
对于每一个Query,输出一个整数,表示询问的答案,并精确到整百元(以百元为单位,例如:该天最大收益为 210 或 290 时,均应该输出 2)。没有方案时回答询问要输出 0。
输入输出样例
吐槽:这个样例给了跟没给有啥区别?
输入样例#1:
10 Project 5.10200 0.65000 Project 2.76200 1.43000 Query 4 Query 2 Project 3.80200 1.17000 Query 2 Query 3 Query 1 Project 4.58200 0.91000 Project 5.36200 0.39000
输出样例#1:
0 0 0 0 0
说明
数据范围:
1 \leq N \leq 100000, 1 \leq T \leq 50000, 0 < P < 100, |S| \leq 10^5
提示:
本题读写数据量可能相当巨大,请选手注意选择高效的文件读写方式。
题解
这个要用到线段树的标记永久化用法。
标记永久化
标记永久化是指一个标记打到区间上以后,不再下放(即pushdown),而是由查询的时候向上查询标记并更新答案。
模型转化
这里相当于加入若干直线,并且询问x坐标固定时y坐标最大的值。我们考虑让线段树中存下这些直线在每个区间对应的中点值最大的线段(这里的线段是抽象说法,而非实现写法)。对于插入一根直线,我们考虑这根直线跟现在已有的直线的关系。如下图,共有4种情况:
黑色为已有直线,蓝色为待加入直线。
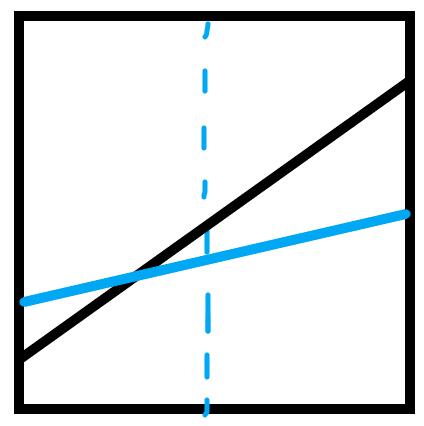
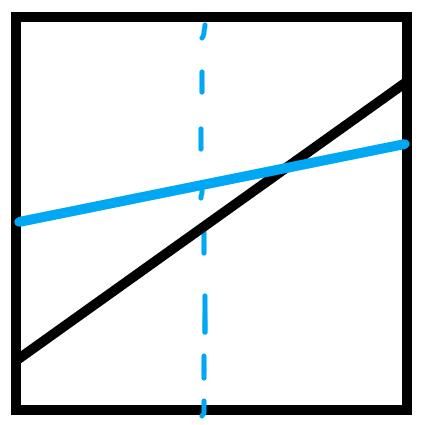
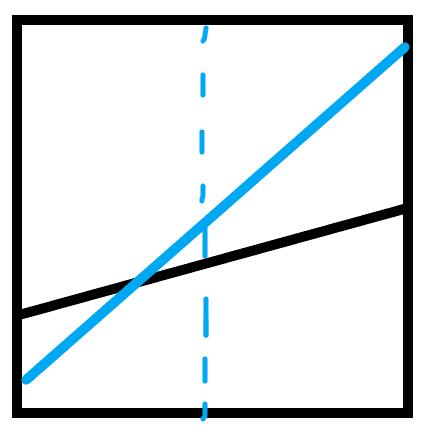
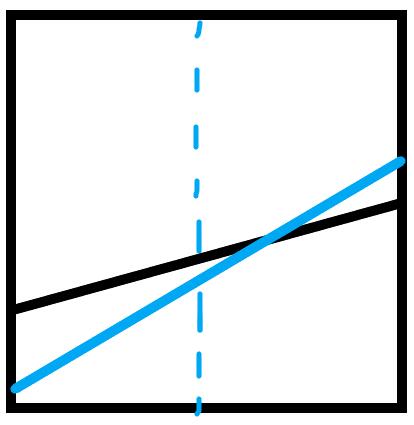
对于每种情况,我们把中点值大的直线存在这个区间,并且把有交点的那一半区间递归下去处理。
查询时,从该点往上找,更新区间存的直线该点的函数值。
代码
// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while (c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline double readdemi() {
register double res = 0;
register int siz = 0, neg = 1;
register bool indem = false;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while ((c >= '0' && c <= '9') || c == '.') {
if(c == '.') {
indem = true;
c = fgc();
continue;
}
if(indem) siz++;
res = res * 10 + c - '0';
c = fgc();
}
while(siz--) res /= 10;
return res * neg;
}
const int MAXN = 50005, N = 50000, MAXM = 100005;
inline bool isop(char c) {
return c == 'P' || c == 'Q';
}
inline char readop() {
char c = fgc();
while (!isop(c)) c = fgc();
return c;
}
int q, t;
char op;
double s[MAXM], p[MAXM];
int ptot = 1;
inline double cal(int line, int x) {
return s[line] + (x - 1) * p[line];
}
inline bool cmp(int l1, int l2, int x) { // if l1 bigger than l2 on pos x
return cal(l1, x) > cal(l2, x);
}
#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)
int tree[MAXN << 2];
inline void modify(int o, int l, int r, int line) {
if(l == r) {
if(cmp(line, tree[o], l)) tree[o] = line;
return;
}
if(p[line] > p[tree[o]]) {
if(cmp(line, tree[o], mid)) {
modify(lch, l, mid, tree[o]);
tree[o] = line;
} else {
modify(rch, mid + 1, r, line);
}
} else {
if(cmp(line, tree[o], mid)) {
modify(rch, mid + 1, r, tree[o]);
tree[o] = line;
} else {
modify(lch, l, mid, line);
}
}
}
inline double query(int o, int l, int r, int x) {
double res = cal(tree[o], x);
if(l == r) {
return res;
}
if(x <= mid) res = std::max(res, query(lch, l, mid, x));
if(x > mid) res = std::max(res, query(rch, mid + 1, r, x));
return res;
}
int main() {
q = readint();
while(q--) {
op = readop();
if(op == 'P') {
s[ptot] = readdemi();
p[ptot] = readdemi();
modify(1, 1, N, ptot);
ptot++;
}
if(op == 'Q') {
t = readint();
printf("%.0lf\n", floor(query(1, 1, N, t) / 100));
}
}
return 0;
}
