2018年1月4日

网络流24题题解

网络流24题题目可以在洛谷上找到。点击题目标题也可以直接进入该题目。
本题解中只讲到了解决这些问题的一种方法，这种方法可能并非最优的方法，仅是提供一种思维方式，供各位参考。
网络流相关模板：

2018/1/26 完工。

飞行员配对方案问题

一句话题意

求最大匹配。
数据范围：总点数 $< 200$

题解

匈牙利算法的模板。

代码

// Code by KSkun, 2017/12 
#include <cstdio>
#include <cstring>
#include <vector>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') {
            if(*s == '-') neg = -1;
            s++;
        }
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
};

io ip;

#define read ip.read 

std::vector<int> vec[2005]; 

int n, m;
bool vis[2005];
int match[2005];

inline bool dfs(int u) {
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if(!vis[v]) {
            vis[v] = true;
            if(match[v] == -1 || dfs(match[v])) {
                match[v] = u;
                match[u] = v;
                return true;
            }
        }
    }
    return false;
} 

inline int hungarian() {
    int ans = 0;
    memset(match, -1, sizeof match);
    for(int i = 1; i <= n; i++) {
        if(match[i] == -1) {
            memset(vis, 0, sizeof vis);
            if(dfs(i)) ans++;
        }
    }
    return ans;
}

int ut, vt;

int main() {
    m = read();
    n = read();
    for(;;) {
        ut = read();
        vt = read();
        if(ut == -1 && vt == -1) break;
        vec[ut].push_back(vt);
        vec[vt].push_back(ut);
    }
    printf("%d\n", hungarian());
    for(int i = m + 1; i <= n; i++) {
        if(match[i] != -1) printf("%d %d\n", i, match[i]);
    }
    return 0;
}

软件补丁问题

一句话题意

默认这个程序有一些漏洞，给你一些补丁，补丁必须在一些漏洞存在而一些漏洞不存在的时候才能使用，使用后补丁会使一些漏洞被修好，但同时又加入了另外的一些漏洞，每个补丁运行需要一定的时间。求把漏洞完全修好需要的最短时间。
数据范围：补丁数 $\leq 100$ ，漏洞数 $\leq 20$

题解

漏洞数比较小，可以考虑状态压缩最短路。由于补丁存在一些漏洞不作要求，需要建的边可能会很多，因此我们可以在SPFA的过程中枚举补丁来转移，这样反而更快。

代码

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>

const int INF = 0x3f3f3f3f;

struct Fix {
    int time;
    char str1[500], str2[500];
} fixs[105];

std::queue<int> que;
int n, m, t, dis[1 << 21], sta1, sta2;
char str1[500], str2[500];
bool inque[1 << 21];

inline void spfa(int st) {
    memset(dis, 0x3f, sizeof dis);
    memset(inque, 0, sizeof inque);
    que.push(st);
    inque[st] = true;
    dis[st] = 0;
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        inque[u] = false;
        for(int i = 0; i < m; i++) {
            bool success = true;
            for(int j = 0; j < n; j++) {
                if(fixs[i].str1[j] == '+' && !(u & (1 << j))) {
                    success = false;
                    break;
                }
                if(fixs[i].str1[j] == '-' && (u & (1 << j))) {
                    success = false;
                    break;
                }
            }
            if(!success) continue;
            int v = u;
            for(int j = 0; j < n; j++) {
                if(fixs[i].str2[j] == '+' && !(u & (1 << j))) {
                    v |= (1 << j);
                }
                if(fixs[i].str2[j] == '-' && (u & (1 << j))) {
                    v ^= (1 << j);
                }
            }
            if(dis[v] > dis[u] + fixs[i].time) {
                dis[v] = dis[u] + fixs[i].time;
                if(!inque[v]) {
                    inque[v] = true;
                    que.push(v);
                }
            }
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 0; i < m; i++) {
        scanf("%d%s%s", &fixs[i].time, fixs[i].str1, fixs[i].str2);
    }
    spfa((1 << n) - 1);
    printf("%d", dis[0] == INF ? 0 : dis[0]);
    return 0;
}

负载平衡问题

一句话题意

一排仓库按照环形排列，每个仓库里有若干货物，货物可以在相邻的仓库间运输，现在想求最少运输多少货物能够使每个仓库的货物数量相等。
数据范围：仓库数 $\leq 100$

题解

这个题解的思路来自hzwer，这是他的博客。
我们对每个仓库创建两个节点 $X_i$ 和 $Y_i$ ，前者为供应节点，后者为需求节点。求出最终要达到的货物值即平均数，然后把初始值处理成偏移值（初始值-平均数）。

偏移小于0。表明这个节点需要运入货物，将节点的 $X_i$ 与源点 $S$ 相连，容量为偏移，费用为0。
偏移大于0。表明这个节点需要运出货物，将节点的 $Y_i$ 与汇点 $T$ 相连，容量为偏移的绝对值，费用为0。

然后再考虑相邻节点的关系。

相邻节点互相补充。将 $X_i$ 与 $Y_j$ 相连，容量为 $+ \infty$ ，费用为1，表示运输单位货物需要1的费用。
不是直接补充，而是作为中间节点转运。将 $X_i$ 与 $X_j$ 相连，容量为 $+ \infty$ ，费用为1，意义同上。

以以上方式建图跑最小费用最大流即可。最大流保证能够平衡货物，而最小费用流能保证运输的货物最少。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <utility>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 1005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int n, remain[1005], sum = 0, s, t; 

int main() {
    n = read();
    s = n * 2 + 1;
    t = s + 1;
    for(int i = 1; i <= n; i++) {
        remain[i] = read();
        sum += remain[i];
    }
    sum /= n;
    for(int i = 1; i <= n; i++) {
        remain[i] -= sum;
        if(remain[i] < 0) {
            addedge(i + n, t, -remain[i], 0);
        } else {
            addedge(s, i, remain[i], 0);
        }
        if(i - 1 > 0) {
            addedge(i, i - 1, INF, 1);
            addedge(i, i - 1 + n, INF, 1);
        }
        if(i + 1 <= n) {
            addedge(i, i + 1, INF, 1);
            addedge(i, i + 1 + n, INF, 1);
        }
    }
    addedge(1, n, INF, 1);
    addedge(1, n << 1, INF, 1);
    addedge(n, 1, INF, 1);
    addedge(n, 1 + n, INF, 1);
    min_cost_flow(s, t);
    printf("%d", cost);
    return 0;
}

魔术球问题

一句话题意

有n根柱子，每根柱子上可以放入一定数量的球，但只能从最上面往上堆。每个柱子的球要求相邻两个的编号和为完全平方数。求最多能放入多少球
数据范围： $4 \leq n \leq 55$

题解

这个题解的思路来自mjtlyzbsy，这是他的博客。
首先我们考虑如何建图，即表达相邻球之间的关系。
可以将一个球拆点为 $A_i$ 和 $B_i$ ，先从源点 $S$ 向 $A_i$ 连容量为1的边，从 $B_i$ 向汇点连容量为1的边。对于能够与它编号和为完全平方数的球j，连接 $A_j$ 和 $B_i$ 。这样的图有什么特性，在底下的分析中会展现出来。
枚举球数，球数每增加1就建立新加入的球的关系，并且重复地跑最大流。柱子数对于球数存在一种单调递增的相关关系，我们这样可以求出某一柱子数下最多能放置的球数，因为当新加入的球能够加入柱子时，重复跑最大流是能得到新流（即：该球可与其他球构成新的相邻关系）的，只要一直能得到新流，就说明柱子上还可以再加，当有一次得不到新流，就说明柱子满了，新加入的球并没能加入到任何一个柱子上。此时我们就加柱子。直到柱子加到超过n，此时的球数-1就是最大球数（因为此时实际上柱子加到超过n了）。
至于输出每个柱子上的球，我们可以记下第一个加入柱子的球。在DFS得到增广路的过程中，总是记下该点连接的下一个点的球的编号，形成类似链表的结构。最后再取出第一个加入柱子的球，来遍历它所在的那条链。
注释中也有部分说明。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cmath>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

const int MAXN = 1000005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN], pre[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                // u representes the ball number floor(u / 2), and so as v
                pre[u >> 1] = v >> 1;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int n, s = 1000001, t = 1000002, pillar = 0, now = 0, head[10005];
bool vis[1000005];

int main() {
    scanf("%d", &n);
    // add more pillars if possible
    while(pillar <= n) {
        now++; // try to add one more ball
        addedge(s, now << 1, 1);
        addedge((now << 1) | 1, t, 1);
        // find the ball which can connect to this
        for(int i = sqrt(now) + 1; i * i < (now << 1); i++) {
            addedge((i * i - now) << 1, (now << 1) | 1, 1);
        }
        int flow = max_flow(s, t);
        if(!flow) {
            // when it needs to add more pillars, record the first ball added to the next pillar
            head[++pillar] = now;
        }
    }
    printf("%d\n", now - 1);
    for(int i = 1; i <= n; i++) {
        if(!vis[head[i]]) {
            for(int u = head[i]; u != 0 && u != (t >> 1); u = pre[u]) {
                vis[u] = true;
                printf("%d ", u);
            }
            printf("\n");
        }
    }
    return 0;
}

餐巾计划问题

题面

一个餐厅在相继的 $N$ 天里，第 $i$ 天需要 $R_i$ 块餐巾( $1 \leq i \leq N$ )。餐厅可以从三种途径获得餐巾。

购买新的餐巾，每块需 $p$ 分；
把用过的餐巾送到快洗部，洗一块需 $m$ 天，费用需 $f$ 分( $f < p$ )。如 $m = 1$ 时，第一天送到快洗部的餐巾第二天就可以使用了，送慢洗的情况也如此。
把餐巾送到慢洗部，洗一块需 $n$ 天( $n > m$ )，费用需 $s$ 分( $s < f$ )。

在每天结束时，餐厅必须决定多少块用过的餐巾送到快洗部，多少块送慢洗部。在每天开始时，餐厅必须决定是否购买新餐巾及多少，使洗好的和新购的餐巾之和满足当天的需求量 $R_i$ ，并使 $N$ 天总的费用最小
数据范围： $N \leq 2000$

题解

这个题解的思路来自M_sea，题解来自洛谷题解。
首先把每一天看成一个点，然后拆点成 $X_i$ 和 $Y_i$ ，分别表示早上和晚上。
建图规则如下：

从源点 $S$ 向 $X_i$ 建边，容量 $R_i$ ，费用0。
从 $Y_i$ 向汇点 $T$ 建边，容量 $R_i$ ，费用0。1、2两条用来保证这一天有 $R_i$ 的餐巾。这个流一定会跑满，因为最差也可以通过购买获得够这么多餐巾。
新购来的餐巾。从 $S$ 向 $Y_i$ 建边，容量 $+ \infty$ ，费用p。
今天没用掉的餐巾明天接着用。从 $X_i$ 向 $X_{i+1}$ 建边，容量 $+ \infty$ ，费用0。
送去快洗部。从 $X_i$ 向 $Y_{i+m}$ 建边，容量 $+ \infty$ ，费用f。
送去慢洗部。从 $X_i$ 向 $Y_{i+n}$ 建边，容量 $+ \infty$ ，费用s。

由规则我们可以知道 $X_i$ 实际上意义是能得到多少餐巾，而 $Y_i$ 是今天要花多少餐巾（即：结算今天的餐巾）。没到 $Y_i$ 的流就会通过 $X_i$ 到别的天数去。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <utility>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 20005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0;
long long cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += 1ll * f[t] * dis[t];
    }
}

int N, R[20005], p, m, F, n, s, S, T;

int main() {
    N = read();
    S = (N << 1) | 1;
    T = S + 1;
    for(int i = 1; i <= N; i++) {
        R[i] = read();
    }
    p = read();
    m = read();
    F = read();
    n = read();
    s = read();
    for(int i = 1; i <= N; i++) {
        addedge(S, i, R[i], 0);
        addedge(i + N, T, R[i], 0);
        addedge(S, i + N, INF, p);
        if(i + m <= N) addedge(i, i + m + N, INF, F);
        if(i + n <= N) addedge(i, i + n + N, INF, s);
        if(i + 1 <= N) addedge(i, i + 1, INF, 0); 
    } 
    min_cost_flow(S, T);
    printf("%lld", cost);
    return 0;
}

汽车加油行驶问题

题面

给定一个N×N的方形网格，设其左上角为起点◎，坐标(1,1)，X轴向右为正，Y 轴向下为正，每个方格边长为1，如图所示。

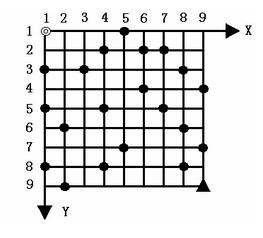
一辆汽车从起点◎出发驶向右下角终点▲，其坐标为(N,N)。
在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

汽车只能沿网格边行驶，装满油后能行驶K条网格边。出发时汽车已装满油，在起点与终点处不设油库。
汽车经过一条网格边时，若其X坐标或Y坐标减小，则应付费用B，否则免付费用。
汽车在行驶过程中遇油库则应加满油并付加油费用A。
在需要时可在网格点处增设油库，并付增设油库费用C(不含加油费用A)。

设计一个算法，求出汽车从起点出发到达终点所付的最小费用。
数据范围： $2 \leq N \leq 100, 2 \leq K \leq 10$

题解

有些人把这种想法叫做分层图，我个人喜欢把它叫做状态空间的转移最短路。
状态由三个量构成(x, y, k)表示坐标在(x, y)且剩余油量为k。那么就从这个点开始，向四周邻近的点来转移，转移的过程中计算费用以及处理加油等。如果下一个点没油站就直接转移or建油站加油，如果下一个点有油站就转移到那个点且油量为K的状态。这里直接求一个最短路就好，在SPFA里处理转移而不需要另外建图。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
#include <utility>

const int INF = 0x3f3f3f3f;

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

struct Point {
    int x, y, k;
    Point(int x, int y, int k): x(x), y(y), k(k) {}
};

std::queue<Point> que;
int dis[105][105][15], fix[5][5] = {{1, 0, -1, 0}, {0, 1, 0, -1}};
bool hasoil[105][105], inque[105][105][15];
int n, K, a, b, c;

inline int getno(int x, int y, int k) {
    return (n * (x - 1) + y - 1) * K + k;
}

inline void spfa(Point s) {
    memset(dis, 0x3f, sizeof dis);
    memset(inque, 0, sizeof inque);
    inque[s.x][s.y][s.k] = true;
    que.push(s);
    dis[s.x][s.y][s.k] = 0;
    while(!que.empty()) {
        Point u = que.front();
        que.pop();
        inque[u.x][u.y][u.k] = false;
        for(int i = 0; i < 4; i++) {
            int vx = u.x + fix[0][i], vy = u.y + fix[1][i], vk = u.k - 1, cost = i < 2 ? 0 : b;
            if(vx <= 0 || vx > n || vy <= 0 || vy > n || vk < 0) continue;
            if(hasoil[vx][vy]) {
                cost += a;
                vk = K;
            }
            if(dis[vx][vy][vk] > dis[u.x][u.y][u.k] + cost) {
                dis[vx][vy][vk] = dis[u.x][u.y][u.k] + cost;
                if(!inque[vx][vy][vk]) {
                    inque[vx][vy][vk] = true;
                    que.push(Point(vx, vy, vk));
                }
            }
            if(!hasoil[vx][vy]) {
                cost += a + c;
                vk = K;
                if(dis[vx][vy][vk] > dis[u.x][u.y][u.k] + cost) {
                    dis[vx][vy][vk] = dis[u.x][u.y][u.k] + cost;
                    if(!inque[vx][vy][vk]) {
                        inque[vx][vy][vk] = true;
                        que.push(Point(vx, vy, vk));
                    }
                }
            }
        }
    }
}

int main() {
    n = read();
    K = read();
    a = read();
    b = read();
    c = read();
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            hasoil[i][j] = read();
        }
    }
    spfa(Point(1, 1, K));
    int ans = INF;
    for(int i = 0; i <= K; i++) {
        ans = std::min(ans, dis[n][n][i]);
    }
    printf("%d", ans);
    return 0;
}

孤岛营救问题

题面

1944年，特种兵麦克接到国防部的命令，要求立即赶赴太平洋上的一个孤岛，营救被敌军俘虏的大兵瑞恩。瑞恩被关押在一个迷宫里，迷宫地形复杂，但幸好麦克得到了迷宫的地形图。迷宫的外形是一个长方形，其南北方向被划分为N行，东西方向被划分为M列，于是整个迷宫被划分为N×M个单元。每一个单元的位置可用一个有序数对(单元的行号，单元的列号)来表示。南北或东西方向相邻的2个单元之间可能互通，也可能有一扇锁着的门，或者是一堵不可逾越的墙。迷宫中有一些单元存放着钥匙，并且所有的门被分成P类，打开同一类的门的钥匙相同，不同类门的钥匙不同。

大兵瑞恩被关押在迷宫的东南角，即(N,M)单元里，并已经昏迷。迷宫只有一个入口，在西北角。也就是说，麦克可以直接进入(1,1)单元。另外，麦克从一个单元移动到另一个相邻单元的时间为1，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。

试设计一个算法，帮助麦克以最快的方式到达瑞恩所在单元，营救大兵瑞恩。
数据范围： $N, M, P \leq 10, K \leq 150, S \leq 14$

题解

跟上面那道题有点相似，只是我们要把在这个点的拥有钥匙的状态给状压一下，用(x, y, S)表示在(x, y)且拥有钥匙的状态为S，然后SPFA最短路跑一通。
注意，起点也有一个可能不为空的拥有钥匙的状态。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>

struct Point {
    int x, y, s;
    Point(int x, int y, int s): x(x), y(y), s(s) {}
};

std::queue<Point> que;
const int fix[5][5] = {{1, -1, 0, 0}, {0, 0, 1, -1}};
int dis[15][15][1 << 10], map[15][15][15][15], key[15][15];
bool inque[15][15][1 << 10];
int N, M, P, K, x1, y1, x2, y2, G;

inline void spfa(Point st) {
    memset(dis, 0x3f, sizeof dis);
    dis[st.x][st.y][st.s] = 0;
    inque[st.x][st.y][st.s] = true;
    que.push(st);
    while(!que.empty()) {
        Point u = que.front();
        que.pop();
        inque[u.x][u.y][u.s] = false;
        for(int i = 0; i < 4; i++) {
            int vx = u.x + fix[0][i], vy = u.y + fix[1][i];
            if(vx <= 0 || vx > N || vy <= 0 || vy > M) continue;
            if(map[u.x][u.y][vx][vy] != -1 && (map[u.x][u.y][vx][vy] == 0 || !(u.s & (1 << (map[u.x][u.y][vx][vy] - 1))))) {
                continue;
            }
            int vs = u.s | key[vx][vy];
            if(dis[vx][vy][vs] > dis[u.x][u.y][u.s] + 1) {
                dis[vx][vy][vs] = dis[u.x][u.y][u.s] + 1;
                if(!inque[vx][vy][vs]) {
                    inque[vx][vy][vs] = true;
                    que.push(Point(vx, vy, vs));
                }
            } 
        }
    }
}

int main() {
    memset(map, -1, sizeof map);
    scanf("%d%d%d%d", &N, &M, &P, &K);
    for(int i = 0; i < K; i++) {
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &G);
        map[x1][y1][x2][y2] = map[x2][y2][x1][y1] = G;
    }
    scanf("%d", &K);
    for(int i = 0; i < K; i++) {
        scanf("%d%d%d", &x1, &y1, &G);
        key[x1][y1] |= (1 << (G - 1));
    }
    spfa(Point(1, 1, key[1][1]));
    int ans = 2e9;
    for(int i = 0; i < (1 << K); i++) {
        ans = std::min(ans, dis[N][M][i]);
    }
    printf("%d", ans == 0x3f3f3f3f ? -1 : ans);
    return 0;
}

星际转移问题

题面

由于人类对自然资源的消耗，人们意识到大约在 2300 年之后，地球就不能再居住了。于是在月球上建立了新的绿地，以便在需要时移民。令人意想不到的是，2177 年冬由于未知的原因，地球环境发生了连锁崩溃，人类（k个）必须在最短的时间内迁往月球。现有n个太空站位于地球与月球之间，且有 m 艘公共交通太空船在其间来回穿梭。每个太空站可容纳无限多的人，而每艘太空船i只可容纳H[i]个人。每艘太空船将周期性地停靠一系列的太空站，例如：(1，3，4)表示该太空船将周期性地停靠太空站 134134134…。每一艘太空船从一个太空站驶往任一太空站耗时均为1。人们只能在太空船停靠太空站(或月球、地球)时上、下船。初始时所有人全在地球上，太空船全在初始站。试设计一个算法，找出让所有人尽快地全部转移到月球上的运输方案。
对于给定的太空船的信息，找到让所有人尽快地全部转移到月球上的运输方案。
数据范围： $n \leq 13, m \leq 20, 1 \leq k \leq 20$

题解

在写这个题的时候，我正儿八经地理解了什么叫做分层。
对于这道题而言，我们把一个时间段看做一层，由于答案是不确定的，所以我们要从最开始一直往后枚举那个答案。枚举的过程中，我们需要建立从本层这段时间的关系，即飞船能带来的改变。由于这里分了层，对于每一层都要建本层的点，月球对答案并无影响，可以看成是汇点T。地球会有不同时间上不同人数的差别，所以应当分开建点，所以每一个状态有n+1个点，要维护好它们的序号。我们把这段时间最初和最末抽象为两个状态。上面提到的关系分为以下几种：

源点到最初的地球，容量INF。
这段时间中飞船从最初的某太空站到最后的某太空站，容量为飞船容量。
由于每个太空站/地球都可能有人没走，需要继承这个状态，对于每个太空站/地球，从最初到最后状态建容量INF边。

每枚举出一层，建一层的边，跑一遍最大流，直到枚举到某一时刻流大于k，就得到了答案。
关于无解的情况，答案极大时可以认为无解。或者用并查集判断一下飞船连不连得起来地球和月球。

代码

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        // fooled by the input of negative number 
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int n, m, k, h[25], r[25], s[25][25], S, T, st;

int main() {
    n = read();
    m = read();
    k = read();
    S = 0;
    T = 1e5;
    for(int i = 1; i <= m; i++) {
        h[i] = read();
        r[i] = read();
        for(int j = 0; j < r[i]; j++) {
            s[i][j] = read();
        }
    }
    register int i, flow = 0;
    // find ans (that is i)
    for(i = 1; i <= 1000; i++) {
        int now = i * (n + 1), lst = (i - 1) * (n + 1);
        // case 1 above
        addedge(S, lst + n + 1, INF);
        for(int j = 1; j <= m; j++) {
            int u = (i - 1) % r[j], v = i % r[j], ut = lst + s[j][u], vt = now + s[j][v];
            if(s[j][u] == -1) ut = T;
            if(s[j][u] == 0) ut = lst + n + 1;
            if(s[j][v] == -1) vt = T;
            if(s[j][v] == 0) vt = now + n + 1;
            // case 2 above
            addedge(ut, vt, h[j]);
        }
        flow += max_flow(S, T);
        if(flow >= k) break;
        for(int j = 1; j <= n + 1; j++) {
            // case 3 above
            addedge(lst + j, now + j, INF); 
        } 
        st += n + 1;
    }
    // if ans is too big, maybe it has no solution
    if(i <= 1000) printf("%d", i); else printf("0");
    return 0;
}

太空飞行计划问题

题面

W教授正在为国家航天中心计划一系列的太空飞行。每次太空飞行可进行一系列商业性实验而获取利润。现已确定了一个可供选择的实验集合E={E1，E2，…，Em}，和进行这些实验需要使用的全部仪器的集合I={I1，I2，…，In}。实验Ej需要用到的仪器是I的子集Rj。配置仪器Ik的费用为ck美元。实验Ej的赞助商已同意为该实验结果支付pj美元。W教授的任务是找出一个有效算法，确定在一次太空飞行中要进行哪些实验并因此而配置哪些仪器才能使太空飞行的净收益最大。这里净收益是指进行实验所获得的全部收入与配置仪器的全部费用的差额。
对于给定的实验和仪器配置情况，编程找出净收益最大的试验计划。
数据范围： $n, m \leq 50$

题解

本题题解相关参考资料及所有图片来源：最大权闭合图 – Because Of You – 博客园。感觉原博主制作图片，所有图片著作权归原博主所有。
这个题引入了最大权闭合图的概念。一个闭合图的定义为图中所有点的出边的终点都在这个图中。一个图的最大权闭合子图为其中所有闭合子图中权值和最大的。
本题的实质就是求最大权闭合图，试按照实验-仪器的关系建图，并将它们的收益（如果要花钱，则为负值）标注在点上。这个图应当形如以下示例。

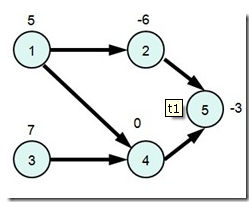
要求本图上的最大权闭合图，就要先将原图中的正值点连向源点S，容量为点权，负值点连向汇点T，容量为点权的绝对值，例如下图示例。

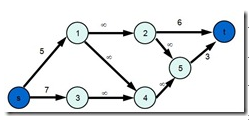
解决问题需要用到以下定理。
定理1 最小割=最大流
定理2 最小割分割成的两个图中，源点S所在的那个图是最大权闭合图。
详细的证明可以参考上面的参考资料。
既然我们知道了这么多，我们就可以得知本题的答案了，就是收益和减去一个最小割。这里最小割的意义实际上是做了亏钱的实验的收益+购买仪器用到的费用。然后输出方案，由于我使用的是Dinic，因此可以看最后一次查出阻塞流的时候有哪些点被BFS遍历到了，如果被遍历到了说明跟源点S在一个子图内。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

const int MAXN = 1000005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN], pre[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                pre[u >> 1] = v >> 1;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int m, n, t, S, T, ans = 0;
char str[10005];

int main() {
    scanf("%d%d", &m, &n);
    S = n + m + 1;
    T = S + 1;
    for(int i = 1; i <= m; i++) {
        scanf("%d", &t);
        ans += t;
        addedge(S, i, t);
        // 洛谷数据太坑 
        memset(str, 0, sizeof str);
        int now = 0;
        std::cin.getline(str, 10000);
        while(sscanf(str + now, "%d", &t) == 1) {
            addedge(i, t + m, INF);
            if(t == 0) {
                now++;
            } else {
                while(t) {
                    t /= 10;
                    now++;
                }
            } 
            now++;
        }
    }
    for(int i = 1; i <= n; i++) {
        scanf("%d", &t);
        addedge(i + m, T, t);
    }
    ans -= max_flow(S, T);
    for(int i = 1; i <= m; i++) {
        if(level[i] != -1) printf("%d ", i);
    }
    printf("\n");
    for(int i = 1; i <= n; i++) {
        if(level[m + i] != -1) printf("%d ", i);
    }
    printf("\n%d", ans);
    return 0; 
}

试题库问题

题面

假设一个试题库中有n道试题。每道试题都标明了所属类别。同一道题可能有多个类别属性。现要从题库中抽取m 道题组成试卷。并要求试卷包含指定类型的试题。试设计一个满足要求的组卷算法。
数据范围： $2 \leq k \leq 20, k \leq n \leq 1000$

题解

本题比较常规，以下是建图思想。

从源点S向每个问题连边，容量为1，控制每个问题最多被用1次。
从问题向每个类型连边，容量对答案没印象，因为已经控制了这个问题用1次。
从每个类型向汇点T连边，容量为该类型所需的试题数，保证这个类型选上的试题数。

首先最大流来一遍看看满不满流，没满就是无解。对Dinic的DFS改动一下，对于上述类型2的那种边记一下类型对应的问题，就是方案了。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

const int MAXN = 1000005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::vector<int> prob[MAXN];
std::queue<int> que;
int level[MAXN];
int k, n, p, t, S, T, sum = 0;

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                if(v >= 1 && v <= k && u > k && u <= k + n) {
                    prob[v].push_back(u - k);
                }
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int main() {
    scanf("%d%d", &k, &n);
    S = k + n + 1;
    T = S + 1;
    for(int i = 1; i <= k; i++) {
        scanf("%d", &t);
        sum += t;
        addedge(i, T, t);
    }
    for(int i = 1; i <= n; i++) {
        scanf("%d", &p);
        while(p--) {
            scanf("%d", &t);
            addedge(i + k, t, 1);
        }
        addedge(S, i + k, 1);
    }
    if(max_flow(S, T) < sum) {
        printf("No Solution!");
    } else {
        for(int i = 1; i <= k; i++) {
            printf("%d: ", i);
            for(int j = 0; j < prob[i].size(); j++) {
                printf("%d ", prob[i][j]);
            }
            printf("\n");
        }
    }
    return 0; 
}

最小路径覆盖问题

题面

给定有向图G=(V,E)。设P是G的一个简单路（顶点不相交）的集合。如果V中每个顶点恰好在P的一条路上，则称P是G的一个路径覆盖。P中路径可以从V的任何一个顶点开始，长度也是任意的，特别地，可以为0。G的最小路径覆盖是G的所含路径条数最少的路径覆盖。设计一个有效算法求一个有向无环图G的最小路径覆盖。
数据范围： $1 \leq n \leq 150, 1 \leq m \leq 6000$

题解

首先，本题要用到以下定理。
定理对于一个有向图，最小点覆盖=顶点数-最大匹配
这里的最大匹配指的是将原图中每一个点拆成入点、出点，每条边连接起点的出点和终点的入点，源点S连接每个点的出点，汇点T连接每个点的入点，这样建出来的二分图的最大匹配。因此我们只要按照题意建图即可。
至于路径，我采取的是记下每个点在路径上的后继点，那些不是任何点的后继点的点自然就是路径的起点了。
相关证明参考：二分图相关定理及其证明（最小点覆盖+最小路径覆盖+最大独立集+最小覆盖集） – CSDN博客

代码

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 1005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN], nxt[MAXN];
int n, m, S, T, ut, vt;
bool vis[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                nxt[u] = v - n;
                vis[v - n] = true;
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int main() {
    n = read();
    m = read();
    S = 2 * n + 1;
    T = S + 1;
    for(int i = 0; i < m; i++) {
        ut = read();
        vt = read();
        addedge(ut, vt + n, 1);
    }
    for(int i = 1; i <= n; i++) {
        addedge(S, i, 1);
        addedge(i + n, T, 1);
    }
    int ans = n - max_flow(S, T);
    for(int i = 1; i <= n; i++) {
        if(!vis[i]) {
            for(int j = i; j != 0; j = nxt[j]) {
                printf("%d ", j);
            }
            printf("\n");
        }
    }
    printf("%d", ans);
    return 0;
}

最长不下降子序列问题

题面

给定正整数序列x1,…,xn。

计算其最长不下降子序列的长度s。
计算从给定的序列中最多可取出多少个长度为s的不下降子序列。
如果允许在取出的序列中多次使用x1和xn，则从给定序列中最多可取出多少个长度为s的不下降子序列。

设计有效算法完成1、2、3提出的计算任务。
数据范围： $n \leq 500$

题解

水题。
对于1， $O(n^2)$ DP解决之。DP值后面有用。
对于2，首先每个元素拆点，建图规则如下。

从源点S向每一个DP值为1的元素入点连边，容量为1，这些元素即为子序列的头。
从每一个DP值为1答案（即LIS长度）的元素出点向汇点T连边，容量为1，这些元素即子序列的尾。
从每个元素拆出来的入点向出点连边，确保每个元素被加入最多一个子序列。
对于任意满足dp[i]==dp[j]+1， $a_j \leq a_i$ 且 $i>j$ 的位置，从j的出点向i的入点连边，容量为1。

对所得图跑最大流，即为答案。
对于3，去除1和n元素的限制即可。一种方法是加入边 $(S, 1), (1, 1 + n), (n, 2n), (2n, T)$ 且容量为INF。然后把上次的残量网络再跑一遍最大流加进2的答案中，得到的就是3的答案。注意，如果n元素不在任何一个LIS中（即dp值不为1的答案），不应该取消n元素的限制。

代码

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 1005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int n, a[505], dp[505], ans = 1, S, T;

int main() {
    n = read();
    for(int i = 1; i <= n; i++) {
        a[i] = read();
    }

    // Prob 1
    dp[1] = 1;
    for(int i = 2; i <= n; i++) {
        dp[i] = 1;
        for(int j = 1; j < i; j++) {
            if(a[j] <= a[i]) dp[i] = std::max(dp[i], dp[j] + 1);
        }
        ans = std::max(ans, dp[i]);
    }
    printf("%d\n", ans);

    // Prob 2
    S = 2 * n + 1;
    T = S + 1;
    for(int i = 1; i <= n; i++) {
        addedge(i, i + n, 1);
        if(dp[i] == ans) addedge(i + n, T, 1);
        if(dp[i] == 1) addedge(S, i, 1);
        for(int j = 1; j < i; j++) {
            if(a[j] <= a[i] && dp[i] == dp[j] + 1) {
                addedge(j + n, i, 1);
            }
        }
    }
    int ans1 = max_flow(S, T);
    printf("%d\n", ans1);

    // Prob 3
    addedge(S, 1, INF);
    addedge(1, 1 + n, INF);
    if(dp[n] == ans) {
        addedge(2 * n, T, INF);
        addedge(n, 2 * n, INF);
    }
    printf("%d", ans1 + max_flow(S, T));
    return 0;
}

航空路线问题

题面

给定一张航空图，图中顶点代表城市，边代表2城市间的直通航线。现要求找出一条满足下述限制条件的且途经城市最多的旅行路线。

从最西端城市出发，单向从西向东途经若干城市到达最东端城市，然后再单向从东向西飞回起点(可途经若干城市)。
除起点城市外，任何城市只能访问1次。

对于给定的航空图，试设计一个算法找出一条满足要求的最佳航空旅行路线。
数据范围： $n < 100$

题解

拆点保证每个点只被使用1次，将来回两条路径转化为去的两条路径，应用最小费用最大流改成最大费用解决这个问题。建图规则如下：

从源点S向1入点连容量2，费用0的边。
从n出点向汇点T连容量2，费用0的边。
对于任意点i从入点向出点连容量1，费用0的边。
对于任意航线(i, j)从i出点向j入点连容量1，费用1的边。

然后直接MCMF一通跑，答案即为花费。如果流跑不满2，就是无解。
至于输出方案，我写的比较丑，就是从S找跑了流的出边，然后从那个边一路如此找到T。复杂度不是很理想，不过数据弱，也跑得过。
另外有一个坑点，最大流为1的时候也有可能是因为只有1到n直接连边可以走，这种情况也是符合题意的，要特判一下。

代码

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <string>
#include <queue>
#include <algorithm>

const int MAXN = 10005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, -1, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] < dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int n, m, S, T;
char str1[50], str2[50];
std::map<std::string, int> map;
std::map<int, std::string> city;
std::vector<int> tmp;

int main() {
    scanf("%d%d", &n, &m);
    S = 2 * n + 1;
    T = S + 1;
    addedge(1, 1 + n, 2, 0);
    addedge(n, n + n, 2, 0);
    for(int i = 1; i <= n; i++) {
        scanf("%s", str1); 
        map[std::string(str1)] = i;
        city[i] = std::string(str1);
        if(i != 1 && i != n) addedge(i, i + n, 1, 0);
    } 
    for(int i = 1; i <= m; i++) {
        scanf("%s%s", str1, str2);
        addedge(map[str1] + n, map[str2], 1, 1);
    }
    min_cost_flow(1, n + n);
    if(flow == 1) {
        bool success = false;
        for(int i = 0; i < vec[1 + n].size(); i++) {
            if(vec[1 + n][i].to == n) {
                success = true;
                break;
            }
        }
        if(success) {
            printf("2\n%s\n%s\n%s\n", city[1].c_str(), city[n].c_str(), city[1].c_str());
            return 0;
        }
    }
    if(flow < 2) {
        printf("No Solution!");
        return 0;
    } 
    printf("%d\n", cost);
    for(int i = 1; i != n;) {
        printf("%s\n", city[i].c_str());
        for(int j = 0; j < vec[i + n].size(); j++) {
            if(vec[i + n][j].cap == 0) {
                i = vec[i + n][j].to;
                break;
            }
        }
    }
    printf("%s\n", city[n].c_str());
    int nxt = -1;
    for(int i = 0; i < vec[1 + n].size(); i++) {
        if(vec[1 + n][i].cap == 0) {
            if(nxt != -1) {
                nxt = vec[1 + n][i].to;
                break;
            } else {
                nxt = vec[1 + n][i].to;
            }
        }
    }
    for(int i = nxt; i != n;) {
        tmp.push_back(i);
        for(int j = 0; j < vec[i + n].size(); j++) {
            if(vec[i + n][j].cap == 0) {
                i = vec[i + n][j].to;
                break;
            }
        }
    }
    for(int i = tmp.size() - 1; i >= 0; i--) {
        printf("%s\n", city[tmp[i]].c_str());
    }
    printf("%s\n", city[1].c_str());
    return 0;
}

方格取数问题

题面

在一个有m*n个方格的棋盘中，每个方格中有一个正整数。现要从方格中取数，使任意2个数所在方格没有公共边，且取出的数的总和最大。试设计一个满足要求的取数算法。对于给定的方格棋盘，按照取数要求编程找出总和最大的数。
数据范围： $m, n \leq 100$

题解

这道题需要一些建模技巧。
我们发现，假如选择了一个方格，必定只影响到其四个相邻的方格，如果应用边/弧来表达这种关系，我们会把整个棋盘建成一个二分图，每相邻的两个点分别在二分图的两个集合中。如果单向地来建图，并且指定一种点作为流的入点，另外一种即为出点，求这样的图的最小割，就能求出最大选法了。
由此我们得到了建图规则：

从源点S向二分图的一个集合中的所有点连边，容量为该点数字大小。
从二分图的另一集合中的所有点向汇点T连边，容量为该点数字大小。
从S连接的那个集合的所有点向其相邻的点连边（相邻点必在另一集合中），容量为INF。

我们发现，建好以后的图的最小割能保证割完的图中不存在相邻点，最小割的容量即为不选的点的数字和，用总和减一下就得到了答案。

代码

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int m, n, mmp[105][105], sum = 0, S, T, fix[5][5] = {{1, -1, 0, 0}, {0, 0, 1, -1}};

inline int getno(int x, int y) {
    return (x - 1) * n + y; 
}

int main() {
    m = read();
    n = read();
    S = m * n + 1;
    T = S + 1; 
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            mmp[i][j] = read(); 
            sum += mmp[i][j];
        }
    }
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            if((i + j) & 1) {
                addedge(S, getno(i, j), mmp[i][j]);
                for(int k = 0; k < 4; k++) {
                    int x = i + fix[0][k], y = j + fix[1][k];
                    if(x < 1 || x > m || y < 1 || y > n) continue;
                    if((i + j) & 1) {
                        addedge(getno(i, j), getno(x, y), INF);
                    }
                }
            } else {
                addedge(getno(i, j), T, mmp[i][j]);
            }
        }
    }
    printf("%d", sum - max_flow(S, T));
    return 0; 
}

圆桌问题

题面

假设有来自n个不同单位的代表参加一次国际会议。每个单位的代表数分别为ri(i=1,2,……,n)。
会议餐厅共有m张餐桌，每张餐桌可容纳ci(i=1,2,……,m)个代表就餐。
为了使代表们充分交流，希望从同一个单位来的代表不在同一个餐桌就餐。试设计一个算法，给出满足要求的代表就餐方案。
对于给定的代表数和餐桌数以及餐桌容量，编程计算满足要求的代表就餐方案。
数据范围： $1 \leq n \leq 270, 1 \leq m \leq 190$

题解

本题要做的事情就是把代表和餐桌对应起来，但又不是一个二分图匹配问题（一个单位可以匹配多个餐桌）。但是我们可以考虑类似的思路。由于每个餐桌只能出现每个单位的1个代表，单位与餐桌之间的关系可以用容量为1的弧来表达。建图规则如下：

从源点S向每一个单位连容量ri的边。
从每个单位向每个餐桌连容量为1的边。
从每个餐桌向汇点T连容量ci的边。

跑最大流，若为满流就说明有解。每个单位的出弧如果跑满了说明那个餐桌被使用了，以此输出方案。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t) return left;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                return d;
            }
        }
    }
    return 0;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int n, m, t, S, T, sum = 0;

int main() {
    n = read();
    m = read();
    S = n + m + 1;
    T = S + 1;
    for(int i = 1; i <= n; i++) {
        t = read();
        sum += t;
        addedge(S, i, t);
        for(int j = 1; j <= m; j++) {
            addedge(i, j + n, 1);
        }
    }
    for(int i = 1; i <= m; i++) {
        t = read();
        addedge(i + n, T, t);
    }
    if(max_flow(S, T) < sum) {
        printf("0");
        return 0;
    }
    printf("1\n");
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j < vec[i].size(); j++) {
            if(vec[i][j].cap == 0) {
                printf("%d ", vec[i][j].to - n);
            }
        }
        printf("\n");
    }
    return 0; 
}

骑士共存问题

题面

在一个n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。

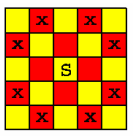
对于给定的n*n个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。
数据范围： $1 \leq n \leq 200, 0 \leq m \leq n^2$

题解

这个题和上面的方格取数问题比较像。可以发现马能跳到的格子跟马所在的格子不是一类格子（有公共边的格子定义为不是一类格子，一个方格图可以划分成两类格子）。因此采用类似的建图方法。

从源点S向一类格子连边，容量1。
从另一类格子向汇点T连边，容量1。
从每一个非障碍的与S相连的格子向其能跳到的格子连边，容量INF。

对这样的图求最小割，割掉的就是不可以放置的位置。答案为所有位置-障碍数-最小割的容量。
另外这个题有一点小小的卡常，在Dinic的DFS可以加一点优化。比如从一个点跑完能扩展的所有增光路（多路增广），以及不继续向已经有流经过的点跑流了（它已经不存在可以增广的余量，本题中这个图的性质）。详细比对一下这个题的Dinic和上面的Dinic有什么不同吧。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 80005;
const int INF = 1e9;

struct Edge {
    int to, cap, rev;
    Edge(int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int level[MAXN];
bool vis[MAXN];

inline void addedge(int u, int v, int cap) {
    vec[u].push_back(Edge(v, cap, vec[v].size()));
    vec[v].push_back(Edge(u, 0, vec[u].size() - 1));
}

// Dinic 

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof level);
    level[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int u = que.front();
        que.pop();
        for(int i = 0; i < vec[u].size(); i++) {
            int v = vec[u][i].to;
            if(level[v] == -1 && vec[u][i].cap > 0) {
                level[v] = level[u] + 1;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

inline int dfs(int u, int t, int left) {
    if(u == t || left == 0) return left;
    int flow = 0;
    vis[u] = true;
    for(int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i].to;
        if(!vis[v] && vec[u][i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, vec[u][i].cap));
            if(d > 0) {
                vec[u][i].cap -= d;
                vec[v][vec[u][i].rev].cap += d;
                left -= d;
                flow += d;
                if(left == 0) {
                    level[u] = -1;
                    return flow;
                }
            }
        }
    }
    return flow;
}

inline int max_flow(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        memset(vis, 0, sizeof vis);
        int f;
        while((f = dfs(s, t, INF)) > 0) {
            flow += f;
        }
    }
    return flow;
}

int m, n, xt, yt, S, T;
const int fix[10][10] = {{-2, -1, -2, -1, 2, 1, 2, 1}, {-1, -2, 1, 2, -1, -2, 1, 2}};
bool mmp[205][205];

inline int getno(int x, int y) {
    return (x - 1) * n + y; 
}

int main() {
    n = read();
    m = read();
    S = n * n + 1;
    T = S + 1; 
    for(int i = 1; i <= m; i++) {
        xt = read();
        yt = read();
        mmp[xt][yt] = true;
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(!mmp[i][j]) {
                if((i + j) & 1) {
                    addedge(S, getno(i, j), 1);
                    for(int k = 0; k < 8; k++) {
                        int x = i + fix[0][k], y = j + fix[1][k];
                        if(mmp[x][y] || x < 1 || x > n || y < 1 || y > n) continue;
                        addedge(getno(i, j), getno(x, y), INF);
                    }
                } else {
                    addedge(getno(i, j), T, 1);
                }
            }
        }
    }
    printf("%d", n * n - m - max_flow(S, T));
    return 0; 
}

火星探险问题

题面

火星探险队的登陆舱将在火星表面着陆，登陆舱内有多部障碍物探测车。登陆舱着陆后，探测车将离开登陆舱向先期到达的传送器方向移动。探测车在移动中还必须采集岩石标本。每一块岩石标本由最先遇到它的探测车完成采集。每块岩石标本只能被采集一次。岩石标本被采集后，其他探测车可以从原来岩石标本所在处通过。探测车不能通过有障碍的地面。本题限定探测车只能从登陆处沿着向南或向东的方向朝传送器移动，而且多个探测车可以在同一时间占据同一位置。如果某个探测车在到达传送器以前不能继续前进，则该车所采集的岩石标本将全部损失。
用一个P×Q网格表示登陆舱与传送器之间的位置。登陆舱的位置在(1, 1)处，传送器的位置在(P, Q)（此处P指列数Q指行数）。
给定每个位置的状态，计算探测车的最优移动方案，使到达传送器的探测车的数量最多，而且探测车采集到的岩石标本的数量最多。
数据范围： $n, p, q \leq 35$

题解

这个题是一个在方格图上建网络的模型。拆点以加入对障碍、岩石的信息这个已经是常见套路了。但是这题有两个量，首先保证探测车数量最多，其次保证岩石标本最多。这让我们想到了最大费用最大流。考虑以车为流岩石标本为费用来跑MCMF，得到的即为最优方案。于是我们就有下面的建图规则：

从源点S向(1, 1)连容量为总车数，费用0的边。
从每个点的出点向相邻右方、下方的点的入点连容量INF，费用0的边。
对于一个障碍点，不对出入点连边。
对于一个非障碍点，从入点向出点连容量INF，费用0的边。
对于一个有岩石标本的点，在4之后再连接一条容量1，费用1的边。这个边一定会在MCMF时比4边先跑到，而且能保证每个标本只被采集一次。
从(p, q)的出点向汇点T连容量INF，费用0的边。（也可以以(p, q)的出点直接作为汇点T）

建图跑MCMF，得到一个跑过流的残量网络。考虑在网络上DFS，每次找反边容量不为0的相邻点，DFS过去即可。这里DFS有一些小细节，比如看到T就终止，找到一个可行点的DFS过去后就不找了，以及每次找完把反边容量减1，表示已经找过一次。具体实现可以参考代码。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <utility>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 10005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, -1, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] < dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int no = 1;

int n, p, q, t, N, S, T; 

inline int getno(int x, int y) {
    return (x - 1) * q + y;
}

inline std::pair<int, int> getpos(int no) {
    if(no > N) no -= N;
    if(no % q) return std::make_pair(no / q + 1, no % q);
    else return std::make_pair(no / q, q);
}

int fix[5][5] = {{1, 0}, {0, 1}};

inline void dfs(int u, int x, int y) {
    for(int i = 0; i < vec[u + N].size(); i++) {
        int v = vec[u + N][i].to;
        if(v == T) break;
        if(vec[v][vec[u + N][i].rev].cap > 0) {
            std::pair<int, int> nxt = getpos(v);
            if(nxt.first != x + 1 && nxt.second != y + 1) continue;
            printf("%d %d\n", no, nxt.first > x ? 0 : 1);
            vec[v][vec[u + N][i].rev].cap--;
            dfs(v, nxt.first, nxt.second);
            break;
        }
    }
}

int main() {
    n = read();
    q = read();
    p = read();
    N = p * q;
    S = N + N + 1;
    T = S + 1;
    addedge(S, getno(1, 1), n, 0); // case 1
    for(int i = 1; i <= p; i++) {
        for(int j = 1; j <= q; j++) {
            t = read();
            if(i + 1 <= p) addedge(getno(i, j) + N, getno(i + 1, j), INF, 0); // case 2
            if(j + 1 <= q) addedge(getno(i, j) + N, getno(i, j + 1), INF, 0); // case 2
            if(t != 1) {
                addedge(getno(i, j), getno(i, j) + N, INF, 0); // case 4
            }
            if(t == 2) {
                addedge(getno(i, j), getno(i, j) + N, 1, 1); // case 5
            }
        }
    }
    addedge(getno(p, q) + N, T, INF, 0); // case 6
    min_cost_flow(S, T);
    while(n--) {
        dfs(1, 1, 1); // dfs
        no++;
    }
    return 0; 
}

最长k可重区间集问题

题面

给定实直线L上n个开区间组成的集合I，和一个正整数k，试设计一个算法，从开区间集合I中选取出开区间集合 $S \subseteq I$ ，使得在实直线L的任何一点x，S中包含点x的开区间个数不超过k，且 $\sum_{z \in S} |z|$ 达到最大，这样的集合S称为开区间集合I的最长k可重区间集， $\sum_{z \in S} |z|$ 称为最长k可重区间集的长度。
对于给定的开区间集合I和正整数k，计算开区间集合I的最长k可重区间集的长度。
数据范围： $1 \leq n \leq 500, 1 \leq k \leq 3$

题解

我们既要限制k可重，又要求出区间长，涉及两个量可以选择最大费用最大流。考虑用流量限制k，而每个开区间长作为区间对应弧的费用。
首先对区间端点坐标离散化，对于离散化后的这些点，相邻点连容量INF，费用0的边，这些边将作为联系区间弧的桥梁。对于每个区间，从左端点到右端点连接流量1，费用为原始区间长度的边，确保只被选择1次且选上后将本区间的长度加入答案。另外源点S到最左点连容量k，费用0的边，控制k可重。可以考虑直接以最右点作为汇点T。对于这样的图跑MCMF，最大费用既为答案。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
typedef long long LL;

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN];
LL dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0;
LL cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, -1, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] < dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += 1ll * f[t] * dis[t];
    }
}

struct Seg {
    int l, r, len;
    Seg(int l, int r): l(l), r(r) {
        len = r - l;
    }
};

int n, k, lt, rt, S, T;
std::vector<int> tmp;
std::vector<Seg> segs; 

int main() {
    n = read();
    k = read();
    for(int i = 0; i < n; i++) {
        lt = read();
        rt = read();
        if(lt > rt) std::swap(lt, rt);
        tmp.push_back(lt);
        tmp.push_back(rt);
        segs.push_back(Seg(lt, rt));
    }
    std::sort(tmp.begin(), tmp.end());
    tmp.erase(std::unique(tmp.begin(), tmp.end()), tmp.end());
    for(int i = 0; i < segs.size(); i++) {
        segs[i].l = std::lower_bound(tmp.begin(), tmp.end(), segs[i].l) - tmp.begin() + 1;
        segs[i].r = std::lower_bound(tmp.begin(), tmp.end(), segs[i].r) - tmp.begin() + 1;
    }
    S = tmp.size() + 1;
    T = S + 1;
    addedge(S, 1, k, 0);
    for(int i = 0; i < tmp.size(); i++) {
        addedge(i, i + 1, INF, 0);
    }
    for(int i = 0; i < segs.size(); i++) {
        addedge(segs[i].l, segs[i].r, 1, segs[i].len);
    }
    addedge(tmp.size(), T, INF, 0);
    min_cost_flow(S, T);
    printf("%lld", cost);
    return 0;
}

最长k可重线段集问题

题面

给定平面x−O−y上n个开线段组成的集合I，和一个正整数k。试设计一个算法，从开线段集合I中选取出开线段集合 $S \subseteq I$ ,使得在x轴上的任何一点p，S中与直线x=p相交的开线段个数不超过k，且 $\sum_{z \in S} |z|$ 达到最大。这样的集合S称为开线段集合I的最长k可重线段集。 $\sum_{z \in S} |z|$ 称为最长k可重线段集的长度。
对于任何开线段z，设其断点坐标为 $(x_0,y_0)$ 和 $(x_1,y_1)$ ，则开线段z的长度|z|定义为：
$|z| = \left \lfloor \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2} \right \rfloor$
对于给定的开线段集合I和正整数k，计算开线段集合I的最长k可重线段集的长度。
数据范围： $1 \leq n \leq 500, 1 \leq k \leq 13$

题解

这个题只是把最长k可重区间集问题的开区间改成了开线段。关于最长k可重区间集问题的做法不再赘述，可以自行上翻到上面看，这里的解释基于该做法。
我们想一下区间变成线段带来了什么变化：首先是长度的求法变了，这个不会对建模产生影响。能产生影响的是线段是可以垂直于x轴的。这就意味着当我们以线段的左右端点x坐标连边时会遇到x坐标相同的情况，这显然是不应出现的。我们采用拆点的策略解决这个问题。假如拆出来的点分别是X点和Y点如果x坐标相同，就从X向Y连，否则从Y向X连。其他的部分与上面那个题相同。

代码

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <algorithm>
typedef long long LL;

struct io {
    char buf[1 << 26], *s;

    io() 
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline LL read() {
        register LL res = 0, neg = 1;
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 1000005;
const int INF = 2e9;

struct Edge {
    LL to, cap, cost, rev;
    Edge(int to, LL cap, LL cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
LL f[MAXN];
int pre[MAXN], pree[MAXN];
LL dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, LL cap, LL cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

LL flow = 0, cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += 1ll * f[t] * dis[t];
    }
}

struct Seg {
    LL l, r, len;
    Seg(LL x1, LL x2, LL len): l(x1), r(x2), len(len) {}
};

inline LL getlen(LL x1, LL y1, LL x2, LL y2) {
    return floor(sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)));
}

LL n, k, xa, xb, ya, yb, S, T, N;
std::vector<LL> tmp;
std::vector<Seg> segs; 

int main() {
    n = read();
    k = read();
    for(int i = 0; i < n; i++) {
        xa = read();
        ya = read();
        xb = read();
        yb = read();
        LL len = getlen(xa, ya, xb, yb);
        if(xa > xb) {
            std::swap(xa, xb);
        }
        xa <<= 1;
        xb <<= 1;
        if(xa == xb) xb |= 1; else xa |= 1; // 这里就是拆点 
        tmp.push_back(xa);
        tmp.push_back(xb);
        segs.push_back(Seg(xa, xb, len));
    }
    std::sort(tmp.begin(), tmp.end());
    N = std::unique(tmp.begin(), tmp.end()) - tmp.begin();
    for(int i = 0; i < segs.size(); i++) {
        segs[i].l = std::lower_bound(tmp.begin(), tmp.begin() + N, segs[i].l) - tmp.begin() + 1;
        segs[i].r = std::lower_bound(tmp.begin(), tmp.begin() + N, segs[i].r) - tmp.begin() + 1;
    }
    S = N + 1;
    T = S + 1;
    addedge(S, 1, k, 0);
    for(int i = 0; i < N; i++) {
        addedge(i, i + 1, INF, 0);
    }
    for(int i = 0; i < segs.size(); i++) {
        addedge(segs[i].l, segs[i].r, 1, -segs[i].len);
    }
    addedge(N, T, INF, 0);
    min_cost_flow(S, T);
    printf("%lld", -cost);
    return 0;
}

深海机器人问题

题面

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。
本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。用一个P×Q网格表示深海机器人的可移动位置。西南角的坐标为(0,0)，东北角的坐标为(Q,P)。
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。计算深海机器人的最优移动方案，使深海机器人到达目的地后，采集到的生物标本的总价值最高。
数据范围： $1 \leq P, Q \leq 15, 1 \leq a \leq 4, 1 \leq b \leq 6$

题解

这个题跟火星探险问题的模型和思路一模一样，因此可以到上面去参考该题题解。
需要注意的是本题是多汇点问题，需要连入同一汇点跑流。以及价值由点上转移到了边上，因此可以认为不需要拆点。

代码

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        //freopen("in.txt", "r", stdin);
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

const int MAXN = 10005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> vec[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int a, b, p, q, t, k, x, y, S, T; 

inline int getno(int x, int y) {
    return x * (q + 1) + y;
}

int main() {
    a = read();
    b = read();
    p = read();
    q = read();
    S = (p + 1) * (q + 1) + 1;
    T = S + 1; 
    for(int i = 0; i <= p; i++) {
        for(int j = 0; j < q; j++) {
            t = read();
            addedge(getno(i, j), getno(i, j + 1), INF, 0);
            addedge(getno(i, j), getno(i, j + 1), 1, -t);
        } 
    } 
    for(int j = 0; j <= q; j++) {
        for(int i = 0; i < p; i++) {
            t = read();
            addedge(getno(i, j), getno(i + 1, j), INF, 0);
            addedge(getno(i, j), getno(i + 1, j), 1, -t);
        } 
    } 
    while(a--) {
        k = read();
        x = read();
        y = read();
        addedge(S, getno(x, y), k, 0);
    }
    while(b--) {
        k = read();
        x = read();
        y = read();
        addedge(getno(x, y), T, k, 0);
    }
    min_cost_flow(S, T);
    printf("%d", -cost);
}

数字梯形问题

题面

给定一个由n行数字组成的数字梯形如下图所示。

梯形的第一行有m个数字。从梯形的顶部的m个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。
分别遵守以下规则：

从梯形的顶至底的m条路径互不相交；
从梯形的顶至底的m条路径仅在数字结点处相交；
从梯形的顶至底的m条路径允许在数字结点相交或边相交。

计算每种规则下的路径上最大数字和，重复经过的点权可以重复计算。
数据范围： $1 \leq n, m \leq 20$

题解

本题我们分开考虑需求，在这里就不像上面那样明确说明建图规则了，因为篇幅可能过大。

子问题1：路径不重

既要保证点不重，又要保证边不重。点不重的做法是拆点，拆出来的点间连容量1，费用为点权的边。边不重的做法是可以到达的点连容量1，费用0的边。然后S向第一排，最后一排向T建容量1，费用0的边，跑MCMF。

子问题2：路径可在点重

只需要保证边不重。因此相比1，我们可以不用拆点添加点重限制了。直接对可以到达的点建容量1，费用现在点点权的边。T上的边要记得容量改INF。跑MCMF。

子问题3：路径可在点、边重

毫无限制。直接把2图上的的边容量改INF。

代码

注：代码采用了3个图分开存的写法，空间上可能比较大。

// Code by KSkun, 2018/1 
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') if((*s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> gra1[MAXN], gra2[MAXN], gra3[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(std::vector<Edge> *vec, int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(std::vector<Edge> *vec, int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int m, n, t, S, T, N; 

inline int getno(int x, int y) {
    return (x - 1) * (m + n - 1) + y; 
}

int main() {
    m = read();
    n = read();
    N = m + n - 1;
    S = 2 * n * N + 1;
    T = S + 1;
    for(int i = 1; i <= m; i++) {
        addedge(gra1, S, getno(1, i), 1, 0);
        addedge(gra2, S, getno(1, i), 1, 0);
        addedge(gra3, S, getno(1, i), 1, 0);
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m + i - 1; j++) {
            t = read();
            addedge(gra1, getno(i, j), getno(i, j) + n * N, 1, -t);
            if(i < n) {
                addedge(gra1, getno(i, j) + n * N, getno(i + 1, j), 1, 0);
                addedge(gra1, getno(i, j) + n * N, getno(i + 1, j + 1), 1, 0);
                addedge(gra2, getno(i, j), getno(i + 1, j), 1, -t);
                addedge(gra2, getno(i, j), getno(i + 1, j + 1), 1, -t);
                addedge(gra3, getno(i, j), getno(i + 1, j), INF, -t);
                addedge(gra3, getno(i, j), getno(i + 1, j + 1), INF, -t);
            } else {
                addedge(gra1, getno(i, j) + n * N, T, 1, 0);
                addedge(gra2, getno(i, j), T, INF, -t);
                addedge(gra3, getno(i, j), T, INF, -t);
            }
        } 
    }
    min_cost_flow(gra1, S, T);
    printf("%d\n", -cost);
    flow = cost = 0;
    min_cost_flow(gra2, S, T);
    printf("%d\n", -cost);
    flow = cost = 0;
    min_cost_flow(gra3, S, T);
    printf("%d\n", -cost);
    return 0;
}

分配问题

题面

有n件工作要分配给n个人做。第i个人做第j件工作产生的效益为 $c_{i, j}$ 。试设计一个将n件工作分配给n个人做的分配方案，使产生的总效益最大或最小。
数据范围： $1 \leq n \leq 100$

题解

二分图最大匹配的模板。最小匹配可考虑将边权取负。

代码

注：代码采用了2个图分开存的写法，空间上可能比较大。

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> gra1[MAXN], gra2[MAXN], gra3[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(std::vector<Edge> *vec, int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(std::vector<Edge> *vec, int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int n, t, S, T;

int main() {
    n = read();
    S = 2 * n + 1;
    T = S + 1;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            t = read();
            addedge(gra1, i, j + n, 1, t);
            addedge(gra2, i, j + n, 1, -t);
        }
    }
    for(int i = 1; i <= n; i++) {
        addedge(gra1, S, i, 1, 0);
        addedge(gra2, S, i, 1, 0);
        addedge(gra1, i + n, T, 1, 0);
        addedge(gra2, i + n, T, 1, 0);
    }
    min_cost_flow(gra1, S, T);
    printf("%d\n", cost);
    flow = cost = 0;
    min_cost_flow(gra2, S, T);
    printf("%d\n", -cost);
    return 0;
}

运输问题

题面

W公司有m个仓库和n个零售商店。第i个仓库有 $a_i$ 个单位的货物；第j个零售商店需要 $b_j$ 个单位的货物。货物供需平衡，即 $\sum_{i=1}^m a_i = \sum_{j=1}^n b_j$ 。从第i个仓库运送每单位货物到第j个零售商店的费用为 $c_{i, j}$ 。
试设计一个将仓库中所有货物运送到零售商店的运输方案，使总运输费用最少或最多。
数据范围： $1 \leq n, m \leq 100$

题解

流量平衡问题。建图规则如下：

从源点S向每个仓库连容量仓库货物，费用0的边，代表仓库的储存。
从每个商店向汇点T连容量货物需求，费用0的边，代表货物的需求。
从每个仓库向每个商店连容量INF，费用 $c_{i, j}$ 的边，代表货物运输。

跑MCMF即可。求最多费用考虑对费用取负。

代码

注：代码采用了2个图分开存的写法，空间上可能比较大。

// Code by KSkun, 2018/1
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0, neg = 1;
        while(*s < '0' || *s > '9') if(*(s++) == '-') neg = -1;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res * neg;
    }
} ip;

#define read ip.read

const int MAXN = 100005;
const int INF = 1e9;

struct Edge {
    int to, cap, cost, rev;
    Edge(int to, int cap, int cost, int rev): to(to), cap(cap), cost(cost), rev(rev) {}
};

std::vector<Edge> gra1[MAXN], gra2[MAXN], gra3[MAXN];
std::queue<int> que;
int f[MAXN];
int pre[MAXN], pree[MAXN], dis[MAXN];
bool inque[MAXN];

inline void addedge(std::vector<Edge> *vec, int u, int v, int cap, int cost) {
    vec[u].push_back(Edge(v, cap, cost, vec[v].size()));
    vec[v].push_back(Edge(u, 0, -cost, vec[u].size() - 1));
}

// SPFA Min Cost Flow

int flow = 0, cost = 0;

inline void min_cost_flow(std::vector<Edge> *vec, int s, int t) {
    for(;;) {
        memset(f, 0, sizeof f);
        memset(dis, 0x3f, sizeof dis);
        memset(inque, 0, sizeof inque);
        while(!que.empty()) que.pop();
        que.push(s);
        dis[s] = 0;
        inque[s] = true;
        f[s] = INF;
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            inque[u] = false; 
            for(int i = 0; i < vec[u].size(); i++) {
                int v = vec[u][i].to;
                if(vec[u][i].cap > 0 && dis[v] > dis[u] + vec[u][i].cost) {
                    pre[v] = u;
                    pree[v] = i;
                    f[v] = std::min(vec[u][i].cap, f[u]);
                    dis[v] = dis[u] + vec[u][i].cost;
                    if(!inque[v]) {
                        que.push(v);
                        inque[v] = true;
                    }
                }
            }
        }
        if(f[t] == 0) break;
        for(int u = t; u != s; u = pre[u]) {
            vec[pre[u]][pree[u]].cap -= f[t];
            vec[u][vec[pre[u]][pree[u]].rev].cap += f[t];
        }
        flow += f[t];
        cost += f[t] * dis[t];
    }
}

int m, n, t, S, T;

int main() {
    m = read();
    n = read();
    S = m + n + 1;
    T = S + 1;
    for(int i = 1; i <= m; i++) {
        t = read();
        addedge(gra1, S, i, t, 0);
        addedge(gra2, S, i, t, 0);
    }
    for(int i = 1; i <= n; i++) { 
        t = read();
        addedge(gra1, i + m, T, t, 0);
        addedge(gra2, i + m, T, t, 0);
    }
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            t = read();
            addedge(gra1, i, j + m, INF, t);
            addedge(gra2, i, j + m, INF, -t);
        }
    }
    min_cost_flow(gra1, S, T);
    printf("%d\n", cost);
    flow = cost = 0;
    min_cost_flow(gra2, S, T);
    printf("%d\n", -cost);
    return 0;
}

机器人路径规划问题（未解决）

题面

机器人 Rob 可在一个树状路径上自由移动。给定树状路径 T 上的起点 s 和终点 t，机器人 Rob 要从 s 运动到 t。树状路径 T 上有若干可移动的障碍物。由于路径狭窄，任何时刻在路径的任何位置不能同时容纳 2 个物体。每一步可以将障碍物或机器人移到相邻的空顶点上。设计一个有效算法用最少移动次数使机器人从 s 运动到 t。对于给定的树 T，以及障碍物在树 T 中的分布情况。计算机器人从起点 s 到终点 t 的最少移动次数。
数据范围：所有数字 $\leq 1000$

说明

本题为一个TMP1R (Tree Motion Planning of 1 Robot)问题的模型，目前的算法需要 $O(n^6)$ 的时间复杂度。你当然可以选择写IDA*之类的方法解决它，或者其他方法。本题是网络流24题这一套题中唯一的一道未能解决的问题，现有算法在搜索引擎中都可搜到。由于本题的网络流解法并不通行，博主在此就没有研究。

代码

注：本代码仅是一张表。

// Code by KSkun, 2018/1
#include <cstdio>

int n;

int main() {
    scanf("%d", &n);
    if(n == 5) printf("3");
    else if(n == 13) printf("30");
    else if(n == 19) printf("20");
    else if(n == 100) printf("3");
    else if(n == 1000) printf("3");
    else printf("5");
    return 0;
}

Author: KSkun

Filed Under: 题解, 算法, 洛谷

Tags: 状态压缩, 最小费用流, 分层图, 二分图匹配, 图论, 最大流, 网络流, 最短路, 二分图

[洛谷1273]有线电视网题解

单调队列原理及其应用

1 thought on “网络流24题题解”

cyl说道：
2023年10月2日上午9:32
%%%
回复

发表回复取消回复

此站点使用Akismet来减少垃圾评论。了解我们如何处理您的评论数据。

网络流24题 题解

一句话题意

题解

代码

一句话题意

题解

代码

一句话题意

题解

代码

一句话题意

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

代码

题面

题解

子问题1：路径不重

子问题2：路径可在点重

子问题3：路径可在点、边重

代码

题面

题解

代码

题面

题解

代码

题面

说明

代码

1 thought on “网络流24题 题解”

发表回复 取消回复

网络流24题题解

1 thought on “网络流24题题解”

发表回复取消回复