题目地址：洛谷：【P2327】[SCOI2005]扫雷 – 洛谷、BZOJ：Problem 1088. — [SCOI2005]扫雷Mine

题目描述

相信大家都玩过扫雷的游戏。那是在一个 n×m 的矩阵里面有一些雷，要你根据一些信息找出雷来。万圣节到了，“余”人国流行起了一种简单的扫雷游戏，这个游戏规则和扫雷一样，如果某个格子没有雷，那么它里面的数字表示和它8连通的格子里面雷的数目。现在棋盘是 n×2 的，第一列里面某些格子是雷，而第二列没有雷，如下图：

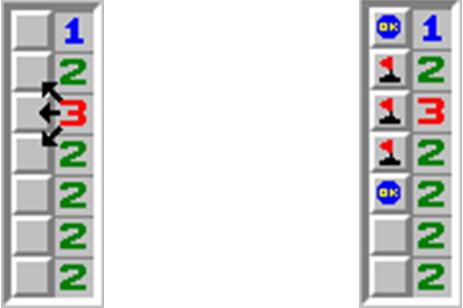
由于第一列的雷可能有多种方案满足第二列的数的限制，你的任务即根据第二列的信息确定第一列雷有多少种摆放方案。

输入输出格式

输入格式：
第一行为N，第二行有N个数，依次为第二列的格子中的数。（1<= N <= 10000）

输出格式：
一个数，即第一列中雷的摆放方案数。

输入输出样例

输入样例#1：

2
1 1

输出样例#1：

2

题解

这道题的解法很多很多，我最开始的想法是存6位状压递推[eq]O(n)[/eq]解，然后特判[eq]n \leq 6[/eq]的情况。
实际上我们发现只需要枚举第一位有没有雷，剩下的位置都唯一确定了，因为一个位置有没有雷可以通过上个位置的数值减去上个位置和上上个位置的雷数得到。也就是说，方案数不会超过2，因此我们枚举第一个位置有没有雷，通过模拟计算下面的情况，如果这个位置要求的雷数非0或1则方案失败。每模拟成功一次计算一个方案。注意模拟的时候要判断末尾是否满足，可以多填一位，再判断n+1位是否有雷多出来了。模拟的复杂度也是[eq]O(n)[/eq]的。

代码

// Code by KSkun, 2018/4
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    register char c = fgc();
    while(!isdigit(c)) {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(isdigit(c)) {
        res = (res << 1) + (res << 3) + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MAXN = 10005;

int n, a[MAXN], has[MAXN];

inline bool cal() {
    for(int i = 2; i <= n + 1; i++) {
        has[i] = a[i - 1] - has[i - 1] - has[i - 2];
        if(has[i] != 0 && has[i] != 1) return false;
        if(i == n + 1 && has[i] != 0) return false;
    }
    return true;
}

int main() {
    n = readint();
    for(int i = 1; i <= n; i++) {
        a[i] = readint();
    }
    int ans = 0;
    if(cal()) ans++;
    memset(has, 0, sizeof(has));
    has[1] = 1;
    if(cal()) ans++;
    printf("%d", ans);
    return 0;
}