题目地址：BZOJ：Problem 5146. — 有趣的概率

题目描述

“可爱的妹子就像有理数一样多，但是我们知道的，你在数轴上随便取一个点取到有理数的概率总是0，”芽衣在床
上自顾自的说着这句充满哲理的话，”诶，柚子，我写完概率论的作业你就和我出去约会怎么样””好呀，但是你要
做完才可以哦”柚子回答道，芽衣立刻从床上翻下来冲到了座位上，诶，就一道题啊，真好，题目是这样的：在一
个圆上任取n个点，求由这n个点依次围成的凸n边形至少有一个锐角的概率是多少，芽衣急于和柚子去约会，当然
没有心情想这一道题，于是她就来求助聪明的你啦。

输入输出格式

输入格式：
一个n,4<=N<=10000000000

输出格式：
至少有一个锐角的概率，为了避免精度问题，对1e9+7取模

输入输出样例

输入样例#1：

136865353

输出样例#1：

423626558

题解

参考资料：【bzoj5146】有趣的概率 微积分 – GXZlegend – 博客园
这个凸多边形的一个锐角的一个邻角必然是钝角，而这个钝角在锐角的逆时针方向的组合只会有一种。我们只研究这两个角。

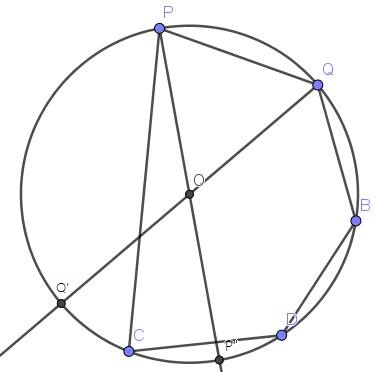
我们看锐角P与钝角Q，设\angle POQ = 2 \pi x，显然这个凸多边形至少有一个点在弧\overgroup{QP'}上，且所有点都分布在弧\overgroup{Q'PQ}上。因此，除了P、Q外其他n-2个点合法的概率为都在弧\overgroup{Q'PQ}上的概率减去都在\overgroup{P'Q'}上的概率，为 (\frac12)^{n-2} - x^{n-2} 。由于x是一个连续的随机变量，我们需要积分出最后的概率。x \in [0, \frac12]，故上述概率为\int_0^{\frac12}((\frac12)^{n-2}-x^{n-2})\mathrm{d}x = \frac{n-2}{n-1}(\frac12)^{n-1}。
注意上述概率是有顺序的，换句话说就是剩余n-2个点的标号已经确定，因此还需要枚举P与Q的标号，即最后的答案是n(n-1) \cdot \frac{n-2}{n-1}(\frac12)^{n-1} = n(n-2)(\frac12)^{n-1}。
注：有标号的意义可以理解为组合数和排列数的区别，即每个点都是不同的，即使它们忽略不同点的分布一致，也视作不同的情况。

代码

// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    char c = fgc();
    while(c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MO = 1e9 + 7;

inline LL fpow(LL n, LL k) {
    LL res = 1;
    while(k) {
        if(k & 1) res = res * n % MO;
        n = n * n % MO;
        k >>= 1;
    }
    return res;
}

LL n;

int main() {
    n = readint() % MO;
    printf("%lld\n", n * (n - 2) % MO * fpow(fpow(2, n - 1), MO - 2) % MO);
    return 0;
}