[HAOI2008]硬币购物 题解
题目地址:洛谷:【P1450】[HAOI2008]硬币购物 – 洛谷、BZOJ …
May all the beauty be blessed.
题目地址:洛谷:【P3172】[CQOI2015]选数 – 洛谷、BZOJ:Problem 3930. — [CQOI2015]选数
我们知道,从区间[L,H](L和H为整数)中选取N个整数,总共有(H-L+1)^N种方案。小z很好奇这样选出的数的最大公约数的规律,他决定对每种方案选出的N个整数都求一次最大公约数,以便进一步研究。然而他很快发现工作量太大了,于是向你寻求帮助。你的任务很简单,小z会告诉你一个整数K,你需要回答他最大公约数刚好为K的选取方案有多少个。由于方案数较大,你只需要输出其除以1000000007的余数即可。
求区间[L, H]中选择N个整数(可重),求选出数组成的可重集gcd为K的方案数%1e9+7的值。
输入格式:
输入一行,包含4个空格分开的正整数,依次为N,K,L和H。
输出格式:
输出一个整数,为所求方案数。
输入样例#1:
2 2 2 4
输出样例#1:
3
样例解释
所有可能的选择方案:(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)
其中最大公约数等于2的只有3组:(2, 2), (2, 4), (4, 2)
对于100%的数据,1<=N,K<=10^9,1<=L<=H<=10^9,H-L<=10^5
参考资料:题解 P3172 【[CQOI2015]选数】 – xyz32768 的博客 – 洛谷博客
我们观察到L与H虽然很大,但是H-L并不大,这是一个我们能利用的地方。首先,可以先行缩小区间范围,即令 L' = \lceil \frac{L}{K} \rceil, H' = \lfloor \frac{H}{K} \rfloor ,问题转变为[L’, H’]区间内选出N个gcd为1的数字的方案数了。
我们考虑一个DP+去重的思想,令f[i]表示含公约数为i且选出的数不全相同的方案数,令[L’, H’]中i的倍数的个数为x,则f[i] = x^n - x。而我们想求的是g[i]表示最大公约数为i且选出的数不全相同的方案数中的g[1],我们容易知道g[i] = f[i] - g[2i] - g[3i] - \cdots,因此可以通过反推求出g[i],从而推得g[1]。f定义中,要求不全相同的原因是如果含相同数字,是因为两两互质肯定不存在选出的数都相同的情况。需要注意的是,如果此L’=1,还可以全选1,因此答案要+1。
// Code by KSkun, 2018/6
#include <cstdio>
#include <cctype>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(!isdigit(c)) {
if(c == '-') neg = -1;
c = fgc();
}
while(isdigit(c)) {
res = (res << 1) + (res << 3) + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005, MO = 1e9 + 7;
inline LL fpow(LL n, LL k) {
LL res = 1;
while(k) {
if(k & 1) res = res * n % MO;
n = n * n % MO;
k >>= 1;
}
return res;
}
LL n, k, l, h, dp[MAXN];
int main() {
n = readint(); k = readint(); l = readint(); h = readint();
if(l % k) l = l / k + 1; else l /= k; h /= k;
if(l > h) {
puts("0"); return 0;
}
for(int i = 1; i <= h - l; i++) {
LL ll = l, hh = h;
if(ll % i) ll = ll / i + 1; else ll /= i; hh /= i;
if(ll > hh) continue;
dp[i] = ((fpow(hh - ll + 1, n) - (hh - ll + 1)) % MO + MO) % MO;
}
for(int i = h - l; i; i--) {
for(int j = i << 1; j <= h - l; j += i) {
dp[i] = ((dp[i] - dp[j]) % MO + MO) % MO;
}
}
if(l == 1) dp[1] = (dp[1] + 1) % MO;
printf("%lld", dp[1]);
return 0;
}
题目地址:洛谷:【P3830】[SHOI2012]随机树 – 洛谷
题面来自洛谷。
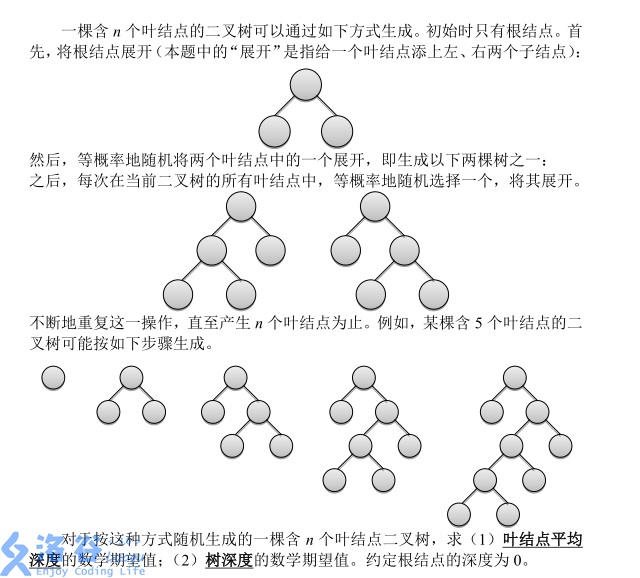
输入格式:
输入仅有一行,包含两个正整数 q, n,分别表示问题编号以及叶结点的个数。
输出格式:
输出仅有一行,包含一个实数 d,四舍五入精确到小数点后 6 位。如果 q = 1,则 d 表示叶结点平均深度的数学期望值;如果 q = 2,则 d 表示树深度的数学期望值。
输入样例#1:
1 4
输出样例#1:
2.166667
输入样例#2:
2 4
输出样例#2:
2.666667
输入样例#3:
1 12
输出样例#3:
4.206421
输入样例#4:
2 12
输出样例#4:
5.916614
2≤n≤100
参考资料:[SHOI2012]随机树 – GuessYCB – 博客园
我们把两个子任务分开看。
第一个求叶节点平均深度的期望,我们令展开i次后这个值为dp[i],则初值dp[1]=0,我们可以利用dp[i-1]来计算dp[i],即将展开的那个叶子节点的深度为dp[i-1],展开后变成了两个dp[i-1]+1深度的叶子,因此转移如下
\begin{aligned} dp[i] &= \frac{dp[i-1] \cdot (i-1) - dp[x-1] + 2(dp[x-1]+1)}{i} \\ &= dp[i-1] + \frac{2}{i} \end{aligned}
由于dp[i]只与dp[i-1]有关,我们甚至不用开数组。
第二个求树高的期望。期望的一种定义是所有情况的和除以情况数,跟展开的情况扯上关系是不好的,因为展开后的形态特别多,没法计算。我们其实并不在意树的形态,而在意树最终有几个儿子,考虑期望的另外一个定义\mathrm{E}(X) = \sum_i \mathrm{P}(X \geq i),我们设计状态dp[i][j]表示有i个叶子的树深度不小于j的概率。转移的时候枚举左子树有多少个叶子,容斥原理计算即可
dp[i][j] = \frac{\sum_{k=1}^{x-1} (dp[k][j-1] + dp[i-k][j-1] - dp[k][j-1] \cdot dp[i-k][j-1])}{x-1}
初始值是dp[i][0]=1。答案就是\sum_{i=1}^{n-1} dp[n][i]。
// Code by KSkun, 2018/4
#include <cstdio>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 105;
int q, n;
double dp[MAXN][MAXN];
int main() {
q = readint(); n = readint();
if(q == 1) {
double res = 0;
for(int i = 2; i <= n; i++) {
res += 2 / double(i);
}
printf("%.6lf", res);
} else {
for(int i = 1; i <= n; i++) dp[i][0] = 1;
for(int i = 2; i <= n; i++) {
for(int j = 1; j < i; j++) {
for(int k = 1; k < i; k++) {
dp[i][j] += dp[k][j - 1] + dp[i - k][j - 1] - dp[k][j - 1]
* dp[i - k][j - 1];
}
dp[i][j] /= i - 1;
}
}
double res = 0;
for(int i = 1; i < n; i++) res += dp[n][i];
printf("%.6lf", res);
}
return 0;
}