北大AC课程2018春测试游记
关于AC课程(中国大学先修课程)是什么,请访问北京大学考试研究院了解。 4月21日 早上回 …
May all the beauty be blessed.
题目地址:洛谷:【P2046】[NOI2010]海拔 – 洛谷、BZOJ:Problem 2007. — [Noi2010]海拔
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域。简单起见,可以将YT市看作 一个正方形,每一个区域也可看作一个正方形。从而,YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路(简称道路),每条双向 道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2×2个区域,包括3×3个交叉路口和12条双向道路。
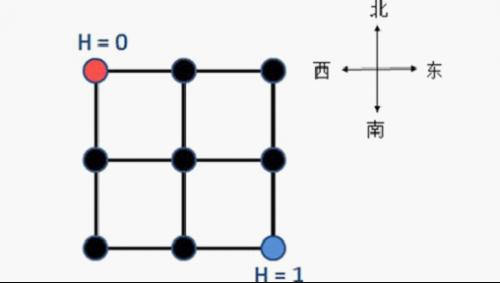
小Z作为该市的市长,他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量,即在高峰期间沿 着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗h的体力。如果 是下坡的话,则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数),那么一个人经过这段路所消耗的体力是max{0, h}(这里max{a, b}表示取a, b两个值中的较大值)。
小Z还测量得到这个城市西北角的交叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡消耗的总体力和的最小值。
输入格式:
第一行包含一个整数n,含义如上文所示。
接下来4n(n + 1)行,每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序:n(n + 1)个数表示所有从西到东方向的人流量,然后n(n + 1)个数表示所有从北到南方向的人流量,n(n + 1)个数表示所有从东到西方向的人流量,最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向,输入顺序按照起点由北向南,若南北方向相同时由西到东的顺序给出(参见样例输入)。
输出格式:
仅包含一个数,表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和(即总体力和的最小值),结果四舍五入到整数。
输入样例#1:
1 1 2 3 4 5 6 7 8
输出样例#1:
3
对于20%的数据:n ≤ 3;
对于50%的数据:n ≤ 15;
对于80%的数据:n ≤ 40;
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
我们发现这些方格在最优解上的高度肯定非0即1,且有一条明显的分界线。因此我们只需要找出一些跨越分界线的边,计算它们的贡献即可。这实际上可以看成一个最小割。
既然我们把原问题转化成了最小割问题,就可以继续转化为对偶图上的最短路问题。由于是方格图,对偶图很好建立。
需要注意的是双向边问题,我们只需要在对偶图上也建立方向相反权值不同的有向边即可。例如我们将向下向右的边建为S→T方向,则向上向左的边要建为T→S方向,随后跑一遍最短路即可。通过验证,S、T的选择与边的方向选择的两种方案是等价的,因此可以任意选择S和T的位置。下面的代码中,上边界和右边界与T相连,下边界和左边界与S相连。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 1000005;
struct Edge {
int to, w, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int w) {
gra[tot] = Edge {v, w, head[u]}; head[u] = tot++;
}
int dis[MAXN];
bool inque[MAXN];
struct Queue {
int l, r, q[MAXN];
inline void clear() {
l = r = 0;
}
Queue() {
clear();
}
inline int front() {
return q[l];
}
inline void push(int x) {
q[r++] = x;
if(r >= MAXN) r -= MAXN;
}
inline void pop() {
l++;
if(l >= MAXN) l -= MAXN;
}
inline bool empty() {
return l == r;
}
} que;
inline void spfa(int s) {
que.clear();
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; inque[s] = true;
que.push(s);
while(!que.empty()) {
register int u = que.front(); que.pop(); inque[u] = false;
for(int i = head[u]; ~i; i = gra[i].nxt) {
register int v = gra[i].to;
if(dis[v] > dis[u] + gra[i].w) {
dis[v] = dis[u] + gra[i].w;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
}
int n, t, S, T;
int main() {
memset(head, -1, sizeof(head));
n = readint();
S = 0; T = n * n + 1;
for(register int i = 1; i <= n + 1; i++) {
for(register int j = 1; j <= n; j++) {
t = readint();
if(i == 1) {
addedge((i - 1) * n + j, T, t);
} else if(i == n + 1) {
addedge(S, (i - 2) * n + j, t);
} else {
addedge((i - 1) * n + j, (i - 2) * n + j, t);
}
}
}
for(register int i = 1; i <= n; i++) {
for(register int j = 1; j <= n + 1; j++) {
t = readint();
if(j == 1) {
addedge(S, (i - 1) * n + j, t);
} else if(j == n + 1) {
addedge((i - 1) * n + j - 1, T, t);
} else {
addedge((i - 1) * n + j - 1, (i - 1) * n + j, t);
}
}
}
for(register int i = 1; i <= n + 1; i++) {
for(register int j = 1; j <= n; j++) {
t = readint();
if(i == 1) {
addedge(T, (i - 1) * n + j, t);
} else if(i == n + 1) {
addedge((i - 2) * n + j, S, t);
} else {
addedge((i - 2) * n + j, (i - 1) * n + j, t);
}
}
}
for(register int i = 1; i <= n; i++) {
for(register int j = 1; j <= n + 1; j++) {
t = readint();
if(j == 1) {
addedge((i - 1) * n + j, S, t);
} else if(j == n + 1) {
addedge(T, (i - 1) * n + j - 1, t);
} else {
addedge((i - 1) * n + j, (i - 1) * n + j - 1, t);
}
}
}
spfa(S);
printf("%d", dis[T]);
return 0;
}
题目地址:BZOJ:Problem 1391. — [Ceoi2008]order
有N个工作,M种机器,每种机器你可以租或者买过来. 每个工作包括若干道工序,每道工序需要某种机器来完成,你可以通过购买或租用机器来完成。 现在给出这些参数,求最大利润
输入格式:
第一行给出 N,M(1<=N<=1200,1<=M<=1200) 下面将有N块数据,每块数据第一行给出完成这个任务能赚到的钱(其在[1,5000])及有多少道工序 接下来若干行每行两个数,分别描述完成工序所需要的机器编号及租用它的费用(其在[1,20000]) 最后M行,每行给出购买机器的费用(其在[1,20000])
输出格式:
最大利润
输入样例#1:
2 3 100 2 1 30 2 20 100 2 1 40 3 80 50 80 110
输出样例#1:
50
如果没有借机器这个项目,本题就是个裸的最大权闭合子图问题。
下面考虑借机器怎么来操作。我们之前的模型是通过割机器-汇点的边来表示购买机器,这条边只能割一次,能不能找到一种边使得每进行涉及该机器的任务的时候都会被割一次。此时我们想到了原来任务-机器之间的无限流的边,只要将这条边的容量设置为借机器的费用,割这条边的时候就代表了借了一次机器。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXN << 5];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
int level[MAXN];
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(level[v] == -1 && gra[i].cap > 0) {
level[v] = level[u] + 1;
if(v == t) return true;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || left <= 0) return left;
int flow = 0;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
left -= d; flow += d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(left <= 0) return flow;
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, m, prof, tc, borr, borc, buyc, S, T, ans;
// 1 ~ n task
// n+1 ~ n+m machine
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint();
S = n + m + 1; T = S + 1;
for(int i = 1; i <= n; i++) {
prof = readint(); tc = readint();
ans += prof;
addedge(S, i, prof);
while(tc--) {
borr = readint(); borc = readint();
addedge(i, borr + n, borc);
}
}
for(int i = 1; i <= m; i++) {
buyc = readint();
addedge(i + n, T, buyc);
}
ans -= dinic(S, T);
printf("%d", ans);
return 0;
}
题目地址:BZOJ:Problem 2561. — 最小生成树
给定一个边带正权的连通无向图G=(V,E),其中N=|V|,M=|E|,N个点从1到N依次编号,给定三个正整数u,v,和L (u≠v),假设现在加入一条边权为L的边(u,v),那么需要删掉最少多少条边,才能够使得这条边既可能出现在最小生成树上,也可能出现在最大生成树上?
输入格式:
第一行包含用空格隔开的两个整数,分别为N和M;
接下来M行,每行包含三个正整数u,v和w表示图G存在一条边权为w的边(u,v)。
最后一行包含用空格隔开的三个整数,分别为u,v,和 L;
数据保证图中没有自环。
输出格式:
输出一行一个整数表示最少需要删掉的边的数量。
输入样例#1:
3 2 3 2 1 1 2 3 1 2 2
输出样例#1:
1
对于20%的数据满足N ≤ 10,M ≤ 20,L ≤ 20;
对于50%的数据满足N ≤ 300,M ≤ 3000,L ≤ 200;
对于100%的数据满足N ≤ 20000,M ≤ 200000,L ≤ 20000。
回想一下最小生成树是怎么来找的,以Kruskal算法为例。我们考虑边权 < L的边,这些边如果能够使u和v连通,则我们想加进去的(u, v, L)这条边就没法加入最小生成树了,因此我们需要删掉一些边权 < L的边,使得u和v不能连通。这个可以用最小割来实现。最大生成树同理。由于我们删掉的边中一些是< L的一些是> L的,这两个集合并无交集,因此不需要去重,直接跑两遍最小割把答案加起来就好。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 20005, MAXM = 400005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXM << 1];
int head[MAXN], tot;
inline void reset() {
memset(head, -1, sizeof(head)); tot = 0;
}
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
int level[MAXN];
std::queue<int> que;
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == -1) {
level[v] = level[u] + 1;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
bool vis[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || !left)
return left;
int flow = 0; vis[u] = true;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && !vis[v] && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
left -= d; flow += d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(!left) {
level[u] = -1;
return flow;
}
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memset(vis, 0, sizeof(vis));
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, m, u, v, w;
struct EData {
int u, v, w;
} edges[MAXM];
int main() {
n = readint(); m = readint();
for(int i = 1; i <= m; i++) {
edges[i].u = readint(); edges[i].v = readint(); edges[i].w = readint();
}
u = readint(); v = readint(); w = readint();
int ans = 0;
reset();
for(int i = 1; i <= m; i++) {
if(edges[i].w < w) {
addedge(edges[i].u, edges[i].v, 1);
addedge(edges[i].v, edges[i].u, 1);
}
}
ans += dinic(u, v);
reset();
for(int i = 1; i <= m; i++) {
if(edges[i].w > w) {
addedge(edges[i].u, edges[i].v, 1);
addedge(edges[i].v, edges[i].u, 1);
}
}
ans += dinic(u, v);
printf("%d", ans);
return 0;
}