【物理】多物体系统的分离问题
本文已弃坑。
例题
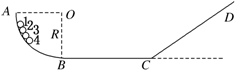
(多选)有一固定轨道ABCD如图所示,AB段为四分之一光滑圆弧轨道,其半径为R,BC段是水平光滑轨道,CD段是光滑斜面轨道,BC和斜面CD间用一小段光滑圆弧连接.有编号为1、2、3、4完全相同的4个小球(小球不能视为质点,其半径r<R),紧挨在一起从圆弧轨道上某处由静止释放,经平面BC到斜面CD上,忽略一切阻力,则下列说法正确的是

A. 四个小球在整个运动过程中始终不分离
B. 当四个小球在圆弧轨道上运动时,2号球对3号球不做功
C. 当四个小球在圆弧轨道上运动时,2号球对3号球做正功
D. 当四个小球在CD斜面轨道上运动时,2号球对3号球做正功
【解析】
这个系统由四个小球组成,其内力的关系非常复杂,对于这类问题,通常整体法是一种比较好的分析思路。本题的过程大致为:系统在斜面上下滑,动能增加→系统经过光滑平面→系统到达右侧斜面,逐小球进入斜面。在进入斜面的过程中,每个小球会发生一定的状态改变,这是我们需要单独考虑的。
A项无论在直觉还是受力分析上都是正确的,故不赘述。
B与C项,我们发现如果只有一个小球从圆弧轨道上滑下,越高的小球滑落到同一高度时速度越快,这是由于高处切线斜率较大,速度增加较快,故此处若不存在3号球,则2号球应当比在系统中运动得更快,则2号球会推着3号球运动,完成一个能量在小球之间的传递过程,C正确。
D项,我们只需要分析该球最大高度可以达到什么位置,若我们取极端数值,令斜面倾角为90°,则排列在斜面上时竖直长度会比在圆弧面上长一些,如果高度一致,则系统重力势能会偏小,因此判断这种极端情况下,最大高度应当比初始位置高一些。
这个问题中不存在小球与系统的完全分离,但是与分离问题具有相似的分析方法,即结合使用整体-隔离法分析能量变化与运动情况,值得参考。
