[JSOI2009]球队收益 题解
题目地址:洛谷:【P4307】[JSOI2009]球队收益 / 球队预算 – …
May all the beauty be blessed.
题目地址:Google Code:Dashboard – Round 2 2014 – Google Code Jam
Aliens have landed. These aliens find our Earth’s rivers intriguing because their home planet has no flowing water at all, and now they want to construct their alien buildings in some of Earth’s rivers. You have been tasked with making sure their buildings do not obstruct the flow of these rivers too much, which would cause serious problems. In particular, you need to determine what the maximum flow that the river can sustain is, given the placement of buildings.
The aliens prefer to construct their buildings on stretches of river that are straight and have uniform width. Thus you decide to model the river as a rectangular grid, where each cell has integer coordinates (X, Y; 0 ≤ X < W and 0 ≤ Y < H). Each cell can sustain a flow of 1 unit through it, and the water can flow between edge-adjacent cells. All the cells on the south side of the river (that is with y-coordinate equal to 0) have an implicit incoming flow of 1. All buildings are rectangular and are grid-aligned. The cells that lie under a building cannot sustain any flow. Given these constraints, determine the maximum amount of flow that can reach the cells on the north side of the river (that is with y-coordinate equal to H-1).
网格图上每个格子可以流经1的流量,流量可以从相邻格子流入或流出到相邻格子。其中有一些矩形区域(互相没有公共部分)不能流。网格图的最后一行每个格子从源流入1的流量,再从网格图的第一行流出。求最大流。
输入格式:
The first line of the input gives the number of test cases, T. T test cases follow. Each test case will begin with a single line containing three integers, W, the width of the river, H, the height of the river, and B, the number of buildings being placed in the river. The next B lines will each contain four integers, X0, Y0, X1, and Y1. X0, Y0 are the coordinates of the lower-left corner of the building, and X1, Y1 are the coordinates of the upper-right corner of the building. Buildings will not overlap, although two buildings can share an edge.
输出格式:
For each test case, output one line containing “Case #x: m”, where x is the test case number (starting from 1) and m is the maximum flow that can pass through the river.
输入样例#1:
2 3 3 2 2 0 2 0 0 2 0 2 5 6 4 1 0 1 0 3 1 3 3 0 2 1 3 1 5 2 5
输出样例#1:
Case #1: 1 Case #2: 2
图形:
两组数据的图形分别如下。
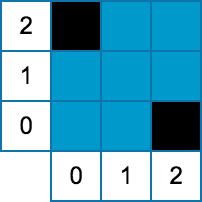
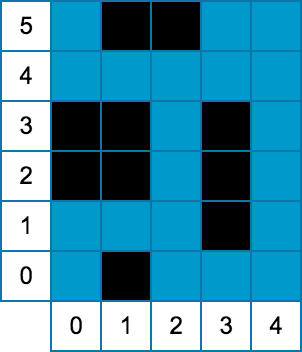
1 ≤ T ≤ 100.
0 ≤ X0 ≤ X1 < W.
0 ≤ Y0 ≤ Y1 < H.
Small dataset
3 ≤ W ≤ 100.
3 ≤ H ≤ 500.
0 ≤ B ≤ 10.
Large dataset
3 ≤ W ≤ 1000.
3 ≤ H ≤ 108.
0 ≤ B ≤ 1000
最大流当然可以直接建图,但是大数据的h比较大,显然直接建图跑不出。我们考虑最大流-最小割定理,将最大流转化为求最小割。由于这个图的特殊性,最小割可以看成从左侧河岸到右侧河岸的最短路。现在我们只需要套一个SPFA上去就能快速解决了。
我们接下来考虑两个矩形之间的最短路怎么计算,可以先画个图。
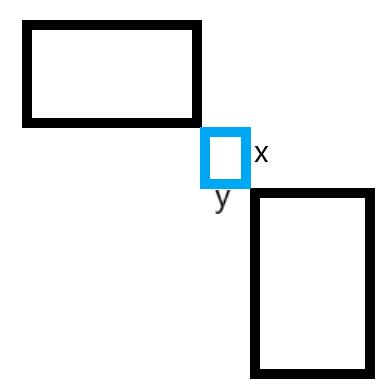
在这个图形中,这两个矩形的最短路实际上是max(x, y)。我们考虑写这样一个函数来计算最短路。
inline int caldis(int u, int v) {
int d1 = std::max(std::max(squ[u].x1 - squ[v].x2, squ[v].x1 - squ[u].x2) - 1, 0);
int d2 = std::max(std::max(squ[u].y1 - squ[v].y2, squ[v].y1 - squ[u].y2) - 1, 0);
return std::max(d1, d2);
}
因为两个矩形的最短路一定是各取左下右上两个点构成图中的蓝色矩形,最短路即为蓝色矩形的长边。上述的d1和d2中的两个max是用于适配u和v矩形的位置关系的。
最好画几个图看下吧。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 1005;
struct Square {
int x1, y1, x2, y2;
} squ[MAXN];
int T, w, h, b, dis[MAXN];
inline int caldis(int u, int v) {
int d1 = std::max(std::max(squ[u].x1 - squ[v].x2, squ[v].x1 - squ[u].x2) - 1, 0);
int d2 = std::max(std::max(squ[u].y1 - squ[v].y2, squ[v].y1 - squ[u].y2) - 1, 0);
return std::max(d1, d2);
}
std::queue<int> que;
bool inque[MAXN];
inline void spfa(int s) {
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; que.push(s); inque[s] = true;
while(!que.empty()) {
int u = que.front(); que.pop(); inque[u] = false;
for(int v = 1; v <= b; v++) {
int d = caldis(u, v);
if(dis[v] > dis[u] + d) {
dis[v] = dis[u] + d;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
}
int main() {
T = readint();
for(int kase = 1; kase <= T; kase++) {
fprintf(stderr, "Processing Case %d\n", kase);
w = readint(); h = readint(); b = readint();
for(int i = 1; i <= b; i++) {
squ[i].x1 = readint(); squ[i].y1 = readint();
squ[i].x2 = readint(); squ[i].y2 = readint();
}
squ[++b] = Square {-1, 0, -1, h - 1};
squ[++b] = Square {w, 0, w, h - 1};
spfa(b - 1);
printf("Case #%d: %d\n", kase, dis[b]);
}
return 0;
}
题目地址:Codeforces:Problem – 311E – Codeforces、洛谷:【CF311E】Biologist – 洛谷
SmallR is a biologist. Her latest research finding is how to change the sex of dogs. In other words, she can change female dogs into male dogs and vice versa.
She is going to demonstrate this technique. Now SmallR has n dogs, the costs of each dog’s change may be different. The dogs are numbered from 1 to n. The cost of change for dog i is vi RMB. By the way, this technique needs a kind of medicine which can be valid for only one day. So the experiment should be taken in one day and each dog can be changed at most once.
This experiment has aroused extensive attention from all sectors of society. There are m rich folks which are suspicious of this experiment. They all want to bet with SmallR forcibly. If SmallR succeeds, the i-th rich folk will pay SmallR wi RMB. But it’s strange that they have a special method to determine whether SmallR succeeds. For i-th rich folk, in advance, he will appoint certain ki dogs and certain one gender. He will think SmallR succeeds if and only if on some day the ki appointed dogs are all of the appointed gender. Otherwise, he will think SmallR fails.
If SmallR can’t satisfy some folk that isn’t her friend, she need not pay him, but if someone she can’t satisfy is her good friend, she must pay g RMB to him as apologies for her fail.
Then, SmallR hope to acquire money as much as possible by this experiment. Please figure out the maximum money SmallR can acquire. By the way, it is possible that she can’t obtain any money, even will lose money. Then, please give out the minimum money she should lose.
有N只狗,性别给定,改变性别花费vi。有M个人,想要让某些狗变成某个性别,如果能满足他们的要求则获得收益wi,否则当这个人是你的朋友的时候则要倒贴g,不是朋友的时候没有倒贴。求最大收益。
输入格式:
The first line contains three integers n, m, g (1 ≤ n ≤ 10^4, 0 ≤ m ≤ 2000, 0 ≤ g ≤ 10^4). The second line contains n integers, each is 0 or 1, the sex of each dog, 0 represent the female and 1 represent the male. The third line contains n integers v1, v2, …, vn (0 ≤ vi ≤ 10^4).
Each of the next m lines describes a rich folk. On the i-th line the first number is the appointed sex of i-th folk (0 or 1), the next two integers are wi and ki (0 ≤ wi ≤ 10^4, 1 ≤ ki ≤ 10), next ki distinct integers are the indexes of appointed dogs (each index is between 1 and n). The last number of this line represents whether i-th folk is SmallR’s good friend (0 — no or 1 — yes).
输出格式:
Print a single integer, the maximum money SmallR can gain. Note that the integer is negative if SmallR will lose money.
输入样例#1:
5 5 9 0 1 1 1 0 1 8 6 2 3 0 7 3 3 2 1 1 1 8 1 5 1 1 0 3 2 1 4 1 0 8 3 4 2 1 0 1 7 2 4 1 1
输出样例#1:
2
输入样例#2:
5 5 8 1 0 1 1 1 6 5 4 2 8 0 6 3 2 3 4 0 0 8 3 3 2 4 0 0 0 3 3 4 1 1 0 10 3 4 3 1 1 0 4 3 3 4 1 1
输出样例#2:
16
我们考虑利用最小割和最大权闭合子图的模型来解决这个问题。
首先对于狗,我们将边的功能定义为割边=变性。因此对于性别0的狗与源连边,性别1的狗与汇连边,容量为变性开销。这是对狗的一次分类。
接下来我们考虑如何处理条件限制。如果用割边来表示不满足一个条件限制,这个是很好做的。关键在于与狗的联系。我们尝试利用类似的方法把条件分类,要求性别为0的条件与源连边,性别1的条件与汇连边,容量为这个条件的收益。对于条件与狗,我们连容量无限的边,表示一种要求,注意有向边的方向,一定要让流可以向不满足条件的狗的方向流,例如性别为0的条件应该向狗连边,而要求性别为1的则要从狗向条件连边。然后我们会发现,与要求条件相同的狗本来就在条件一侧的子图中,这条边永远不会有流流过,而不同的狗则可能有流流过。
我们来思考一条增广路,一定是源→要求0的条件→性别1的狗→汇,割边时要么选择不满足条件,要么选择给狗变性。另外一种情况同理。因此这种建图方式能够满足我们的要求。
此外,还有倒贴的问题。我们可以对条件与源汇连的边加上这个倒贴的g,当用\sum w_i减掉最小割的时候,不能被满足的条件的g也会同时减去。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXN << 5];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
int level[MAXN];
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(level[v] == -1 && gra[i].cap > 0) {
level[v] = level[u] + 1;
if(v == t) return true;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || left <= 0) return left;
int flow = 0;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
left -= d; flow += d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(left <= 0) return flow;
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, m, g, col[MAXN], vi, coli, wi, ki, dogi, fri, ans, S, T;
// 1 ~ n dog
// n+1 ~ n+m rich folk
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint(); g = readint();
S = n + m + 1; T = S + 1;
for(int i = 1; i <= n; i++) {
col[i] = readint();
}
for(int i = 1; i <= n; i++) {
vi = readint();
if(col[i] == 0) addedge(S, i, vi);
else addedge(i, T, vi);
}
for(int i = 1; i <= m; i++) {
coli = readint(); wi = readint(); ki = readint();
ans += wi;
while(ki--) {
dogi = readint();
if(coli == 0) addedge(i + n, dogi, INF);
else addedge(dogi, i + n, INF);
}
fri = readint();
if(coli == 0) addedge(S, i + n, wi + (fri ? g : 0));
else addedge(i + n, T, wi + (fri ? g : 0));
}
ans -= dinic(S, T);
printf("%d", ans);
return 0;
}
题目地址:BZOJ:Problem 2561. — 最小生成树
给定一个边带正权的连通无向图G=(V,E),其中N=|V|,M=|E|,N个点从1到N依次编号,给定三个正整数u,v,和L (u≠v),假设现在加入一条边权为L的边(u,v),那么需要删掉最少多少条边,才能够使得这条边既可能出现在最小生成树上,也可能出现在最大生成树上?
输入格式:
第一行包含用空格隔开的两个整数,分别为N和M;
接下来M行,每行包含三个正整数u,v和w表示图G存在一条边权为w的边(u,v)。
最后一行包含用空格隔开的三个整数,分别为u,v,和 L;
数据保证图中没有自环。
输出格式:
输出一行一个整数表示最少需要删掉的边的数量。
输入样例#1:
3 2 3 2 1 1 2 3 1 2 2
输出样例#1:
1
对于20%的数据满足N ≤ 10,M ≤ 20,L ≤ 20;
对于50%的数据满足N ≤ 300,M ≤ 3000,L ≤ 200;
对于100%的数据满足N ≤ 20000,M ≤ 200000,L ≤ 20000。
回想一下最小生成树是怎么来找的,以Kruskal算法为例。我们考虑边权 < L的边,这些边如果能够使u和v连通,则我们想加进去的(u, v, L)这条边就没法加入最小生成树了,因此我们需要删掉一些边权 < L的边,使得u和v不能连通。这个可以用最小割来实现。最大生成树同理。由于我们删掉的边中一些是< L的一些是> L的,这两个集合并无交集,因此不需要去重,直接跑两遍最小割把答案加起来就好。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 20005, MAXM = 400005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXM << 1];
int head[MAXN], tot;
inline void reset() {
memset(head, -1, sizeof(head)); tot = 0;
}
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
int level[MAXN];
std::queue<int> que;
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == -1) {
level[v] = level[u] + 1;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
bool vis[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || !left)
return left;
int flow = 0; vis[u] = true;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && !vis[v] && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
left -= d; flow += d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(!left) {
level[u] = -1;
return flow;
}
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memset(vis, 0, sizeof(vis));
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
int n, m, u, v, w;
struct EData {
int u, v, w;
} edges[MAXM];
int main() {
n = readint(); m = readint();
for(int i = 1; i <= m; i++) {
edges[i].u = readint(); edges[i].v = readint(); edges[i].w = readint();
}
u = readint(); v = readint(); w = readint();
int ans = 0;
reset();
for(int i = 1; i <= m; i++) {
if(edges[i].w < w) {
addedge(edges[i].u, edges[i].v, 1);
addedge(edges[i].v, edges[i].u, 1);
}
}
ans += dinic(u, v);
reset();
for(int i = 1; i <= m; i++) {
if(edges[i].w > w) {
addedge(edges[i].u, edges[i].v, 1);
addedge(edges[i].v, edges[i].u, 1);
}
}
ans += dinic(u, v);
printf("%d", ans);
return 0;
}