作者： KSkun

2019年10月7日

Popcount问题及算法

问题描述在使用状态压缩或树状数组（Binary Indexed Tree）的时候，经常涉 …

算法, 知识, Slider

by KSkun

0 Comments

2019年9月18日

HUST卓越班选拔上岸记

准备卓越班选拔考试（俗称启明考试）一般在军训一周后的一个周六进行，在这之前有一周的时间（ …

随笔

by KSkun

1 Comment

2019年8月21日

[CF8C]Looking for Order 题解

题目地址：Codeforces：Problem – 8C – Codeforces、洛谷：CF8C Looking for Order – 洛谷 | 计算机科学教育新生态

题目描述

Girl Lena likes it when everything is in order, and looks for order everywhere. Once she was getting ready for the University and noticed that the room was in a mess — all the objects from her handbag were thrown about the room. Of course, she wanted to put them back into her handbag. The problem is that the girl cannot carry more than two objects at a time, and cannot move the handbag. Also, if he has taken an object, she cannot put it anywhere except her handbag — her inherent sense of order does not let her do so.

You are given the coordinates of the handbag and the coordinates of the objects in some Сartesian coordinate system. It is known that the girl covers the distance between any two objects in the time equal to the squared length of the segment between the points of the objects. It is also known that initially the coordinates of the girl and the handbag are the same. You are asked to find such an order of actions, that the girl can put all the objects back into her handbag in a minimum time period.

题意简述

在二维平面上散落着许多物品，你需要把这些物品捡起并放回指定位置的包里，初始时你在包的位置上，你可以移动到任意点，移动的时间为两点间距离的平方，且在任何时候，你的手里最多只能拿不超过2个物品。求把所有物品放回包里的最短时间。

输入输出格式

输入格式：

The first line of the input file contains the handbag’s coordinates x_s, y_s. The second line contains number n (1 ≤ n ≤ 24) — the amount of objects the girl has. The following n lines contain the objects’ coordinates. All the coordinates do not exceed 100 in absolute value. All the given positions are different. All the numbers are integer.

输出格式：

In the first line output the only number — the minimum time the girl needs to put the objects into her handbag.

In the second line output the possible optimum way for Lena. Each object in the input is described by its index number (from 1 to n), the handbag’s point is described by number 0. The path should start and end in the handbag’s point. If there are several optimal paths, print any of them.

输入输出样例

输入样例#1：

输出样例#1：

8
0 1 2 0

输入样例#2：

输出样例#2：

32
0 1 2 0 3 0

题解

数据范围+直觉判断首先得是个状压。

首先从包位置出发，每次选择两个物品，两个物品的先后次序不会影响答案，且不同的两个物品的组合的先后次序也不会影响答案，这条性质会用在之后的一个优化中，现在暂且放在这里。

考虑状压DP，$f(S)$表示已经放进包里的物品的状态为$S$，枚举两个（可以相同，用来表示只拿取了一个物品的情况）不在状态$S$中的物品$i, j$，令包的位置为第0个物品所在位置，$\operatorname{dist}(i, j)$表示从$i$物品到$j$物品所在位置的移动需要的时间，有以下转移

$$ f(S \operatorname{or} 2^{i-1} \operatorname{or} 2^{j-1}) = \min \{ f(S \operatorname{or} 2^{i-1} \operatorname{or} 2^{j-1}), f(S) + \operatorname{dist}(0, i) + \operatorname{dist}(i, j) + \operatorname{dist}(j, 0) \} $$

初始时令所有DP值为极大值，且$f(0)=0$即可。这种算法的复杂度是$O(2^n \cdot n^2)$的，并不能通过本题。

接下来考虑对原算法的优化，由于不同的两个物品的组合的先后次序也不会影响答案，每个物品都必须被拾起取回包中，实际上每次转移只需要找到一个不在$S$中的物品$i$，枚举每一个不在$S$中的物品$j$进行转移就可以了。如果按照以前的逻辑计算，则由于拾取物品$i$的先后次序会很多，答案相同而次序不同的方案会被计算多次，这样优化后只会被计算一次，既保证了答案的正确性又优化了复杂度。

优化后的复杂度是$O(2^n \cdot n)$，由于本题时限设置为4s，还是能通过的。

代码

// Code by KSkun, 2019/8
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>
#include <vector>

typedef long long LL;

inline char fgc() {
	static char buf[100000], * p1 = buf, * p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
		? EOF : *p1++;
}

inline LL readint() {
	LL res = 0, neg = 1; char c = fgc();
	for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
	for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
	return res * neg;
}

inline char readsingle() {
	char c;
	while(!isgraph(c = fgc())) {}
	return c;
}

const int MAXN = 25;
const int INF = 0x3f3f3f3f;

int n, dp[1 << MAXN], pre[1 << MAXN], x[MAXN], y[MAXN], dis[MAXN][MAXN];
std::vector<int> ans;

inline int distance(int a, int b) {
	return (x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]);
}

int main() {
	x[0] = readint(); y[0] = readint();
	n = readint();
	for(int i = 1; i <= n; i++) {
		x[i] = readint(); y[i] = readint();
	}
	for(int i = 0; i <= n; i++) {
		for(int j = i; j <= n; j++) {
			dis[i][j] = dis[j][i] = distance(i, j);
		}
	}
	memset(dp, 0x3f, sizeof(dp));
	dp[0] = 0;
	for(int s = 0; s < (1 << n); s++) {
		if(dp[s] >= INF) continue;
		for(int i = 1; i <= n; i++) {
			if(s & 1 << i - 1) continue;
			for(int j = 1; j <= n; j++) {
				if(s & 1 << j - 1) continue;
				if(dp[s | 1 << i - 1 | 1 << j - 1] > dp[s] + dis[0][i] + dis[i][j] + dis[j][0]) {
					dp[s | 1 << i - 1 | 1 << j - 1] = dp[s] + dis[0][i] + dis[i][j] + dis[j][0];
					pre[s | 1 << i - 1 | 1 << j - 1] = s;
				}
			}
			break;
		}
	}
	printf("%d\n", dp[(1 << n) - 1]);
	int s = (1 << n) - 1;
	while(s) {
		int p = pre[s], t = s ^ p, cnt = 1, t1 = 0, t2 = 0;
		while(t) {
			if((t & 1) == 1) {
				if(t1) t2 = cnt;
				else t1 = cnt;
			}
			t >>= 1; cnt++;
		}
		ans.push_back(0);
		if(t1) ans.push_back(t1);
		if(t2) ans.push_back(t2);
		s = p; p = pre[s];
	}
	ans.push_back(0);
	std::reverse(ans.begin(), ans.end());
	for(auto i : ans) {
		printf("%d ", i);
	}
	return 0;
}

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月19日

[CF7E]Defining Macros 题解

题目地址：Codeforces：Problem – 7E – Co …

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月15日

[CF7D]Palindrome Degree 题解

题目地址：Codeforces：Problem – 7D – Co …

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月11日

[CF6E]Exposition 题解

题目地址：Codeforces：Problem – 6E – Codeforces、洛谷：CF6E Exposition – 洛谷 | 计算机科学教育新生态

题目描述

There are several days left before the fiftieth birthday of a famous Berland’s writer Berlbury. In this connection the local library decided to make an exposition of the works of this famous science-fiction writer. It was decided as well that it is necessary to include into the exposition only those books that were published during a particular time period. It is obvious that if the books differ much in size, the visitors will not like it. That was why the organizers came to the opinion, that the difference between the highest and the lowest books in the exposition should be not more than k millimeters.

The library has n volumes of books by Berlbury, arranged in chronological order of their appearance. The height of each book in millimeters is know, it is h_i. As Berlbury is highly respected in the city, the organizers want to include into the exposition as many books as possible, and to find out what periods of his creative work they will manage to cover. You are asked to help the organizers cope with this hard task.

题意简述

给定一个长度为$n$的数列$h_i$，求该序列中最长的极差不超过$k$的子段（连续一段）长度与数量。你需要输出每一个子段的起止下标。

输入输出格式

输入格式：
The first line of the input data contains two integer numbers separated by a space n (1 ≤ n ≤ 10⁵) and k (0 ≤ k ≤ 10⁶) — the amount of books by Berlbury in the library, and the maximum allowed height difference between the lowest and the highest books. The second line contains n integer numbers separated by a space. Each number h_i (1 ≤ h_i ≤ 10⁶) is the height of the i-th book in millimeters.

输出格式：
In the first line of the output data print two numbers a and b (separate them by a space), where a is the maximum amount of books the organizers can include into the exposition, and b — the amount of the time periods, during which Berlbury published a books, and the height difference between the lowest and the highest among these books is not more than k milllimeters.
In each of the following b lines print two integer numbers separated by a space — indexes of the first and the last volumes from each of the required time periods of Berlbury’s creative work.

输入输出样例

输入样例#1：

3 3
14 12 10

输出样例#1：

2 2
1 2
2 3

输入样例#2：

2 0
10 10

输出样例#2：

2 1
1 2

输入样例#3：

4 5
8 19 10 13

输出样例#3：

2 1
3 4

题解

看到这个题的第一反应就是二分答案，于是转换为判断每个长度为二分出来的值$m$的子段极差，由于极差等于最大值减最小值，维护最大值和最小值是一个滑动窗口问题，可以使用单调队列快速解决。

需要注意的是，本题需要计数并输出方案，因此可以在check函数内维护一个vector装符合要求的子段端点。

总复杂度$O(n \log n)$。

代码

// Code by KSkun, 2019/8
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>
#include <queue>
#include <vector>

typedef long long LL;

inline char fgc() {
	static char buf[100000], * p1 = buf, * p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
		? EOF : *p1++;
}

inline LL readint() {
	LL res = 0, neg = 1; char c = fgc();
	for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
	for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
	return res * neg;
}

inline char readsingle() {
	char c;
	while(!isgraph(c = fgc())) {}
	return c;
}

const int MAXN = 100005;

int n, k, h[MAXN];
std::vector<int> vec;

inline int check(int mid) {
	std::deque<int> mx, mn; vec.clear();
	int cnt = 0;
	for(int i = 1; i < mid; i++) {
		while(!mx.empty() && h[mx.back()] <= h[i]) mx.pop_back();
		while(!mn.empty() && h[mn.back()] >= h[i]) mn.pop_back();
		mx.push_back(i); mn.push_back(i);
	}
	for(int i = mid; i <= n; i++) {
		while(!mx.empty() && h[mx.back()] <= h[i]) mx.pop_back();
		while(!mn.empty() && h[mn.back()] >= h[i]) mn.pop_back();
		mx.push_back(i); mn.push_back(i);
		while(!mx.empty() && mx.front() < i - mid + 1) mx.pop_front();
		while(!mn.empty() && mn.front() < i - mid + 1) mn.pop_front();
		if(h[mx.front()] - h[mn.front()] <= k) {
			cnt++; vec.push_back(i);
		}
	}
	return cnt;
}

int main() {
	n = readint(); k = readint();
	for(int i = 1; i <= n; i++) {
		h[i] = readint();
	}
	h[n + 1] = 1e9;
	int l = 1, r = n + 1, mid;
	while(r - l > 1) {
		mid = (l + r) >> 1;
		if(check(mid)) l = mid;
		else r = mid;
	}
	printf("%d %d\n", l, check(l));
	for(auto i : vec) {
		printf("%d %d\n", i - l + 1, i);
	}
	return 0;
}

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月10日

[CF6D]Lizards and Basements 2 题解

题目地址：Codeforces：Problem – 6D – Co …

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月9日

[CF6A]Triangle 题解

题目地址：Codeforces：Problem – 6A – Co …

题解, 算法, Codeforces

by KSkun

0 Comments

2019年8月6日

Bilibili Macro Link 2019 上海游记

作为一个深受某站文化影响的中二少年，自然是很早就希望去一次这种大型线下**交友活动啦。今年刚好高考完，6月就在各种圈子招募抱团BML的友人，从母上那里拿到了预算，随后约定好票的等级（SP B、VR C），等高考完，就踏上了去上海的奇妙体验的旅程。
这一篇文章主要记录BML一路上的各种见闻和感受。

注：所使用BML现场照片仅包含少量艺人形象，其中，SP场照片全为观众席应援场景，并不包含任何艺人形象，如依然存在侵权问题请与作者联系。

UPD：删除了BML-VR2019艺人相关影像。

7月17日火车上

坐17日的K124从十堰到上海去，24小时左右的长途硬卧，实在算不上什么很好的体验。但是为了省点钱（flag），就这样吧。

带了同济版高数的上册，本来想在火车经过信号不好的区间的时候打发时间用，发现自己的注意力很难集中，估计是利用不了多少时间来学习数学了。不过在钻山洞的一两个小时之内还是看进去了一些东西。
整个车厢里都是带孩子出门旅游的家长，我所在的半包共6个铺位里就有两家子，孩子们玩闹的声音很大，不算是很好的体验。和十堰本地的一家子的家长搭上了话，聊了一些关于学业方面的问题，后来被隔壁的某家长注意到了，然后就开始对我商业吹捧。问题是，我不是那种很正经的人啊？
没办法，要在孩子心目中创造一个好的形象，那就把书读下去呗。小孩子并不怕生，和他们聊了一些生活上的事情，总的来说还算愉快。隔壁家长是所谓的“国学育子”的相关人员，在一旁推销类似的思想，特别想吐槽，不过显然不适合吐槽这个。和她互加了微信，商业互吹一番，在孩子的本子上留下了一句某大大语录，短暂的火车旅程就结束了。

关于所谓“国学育子”：嘛，反正我是不看好这种做法的。隔壁家长的孩子没有几岁就开始阅读《易经》这种层次的古籍，《易》对我来说是一本高深玄妙难以理解的书，自己高中三年的古代文化和文言文理论储备也无法哪怕解读它的一小段文字，这样的内容对于一个孩子来说真的合适吗？如果只是背诵古代典籍中的字词句段，这是一件非常简单的事情，但是哪怕像我一样，经过学习之后能够解读一部分古文的字面意思，对于文言文学习也是远远不够的。我认为，文言文的学习价值不仅局限于它所包含的语言现象，还应该包含文章蕴含的思想、哲理，乃至作者的心理、创作背景，甚至探究古文中反应的社会环境、社会价值等。文字中承载的内容是如此丰富，我一直认为语文是一门有趣的学科，而且享受学习的过程，但这种只求肤浅目标而不求深远价值的做法，只会浪费文章中蕴含的价值，是一种可能造成负面影响的无用功。另外，这不是一种全盘否定，我觉得更好的选择是阅读一些简单易懂的文章，并引导孩子学习围绕文章展开的各种知识。~~呼，吐槽完了，舒服了233~~

7月18日无所事事

一班始发晚点20分钟，途中晚点最多1小时的车，居然第二天可以早点半小时到达中途停站，正点到达终点上海南站。
第二次到上海，第一次在上海玩一玩，这次自然有很多新鲜的发现，例如，弯的地铁站（上海体育馆站）。

在西藏南路站附近预订了汉庭酒店，离地铁站很近，出站后可以直接看到汉庭的招牌。房间意外的小，不过也还算是五脏俱全，比较整洁。可能是由于店比较老，一些设备有故障，这是不尽人意的地方之一，另外一个问题是网速太慢（其实不是长宽都还能忍受啦）。

18日这一天没有安排，于是下午在酒店房间里备课并等无知和M晓到店，与M晓倒不是第一次见但是第一次见无知，都好帅呀www
（没有合照！）
三个人晚上osu!打各种模式的MP，Mania和CTB被血虐，std还好。不过std对我来说还好，对无知和M晓是灾难了，一个没带鼠标一个没有鼠标垫。
来的路上听说了舟游上海“龙门紧急补给点”活动，于是计划着第二天和绿鸽鸽（AntiLeaf，以下皆称绿鸽鸽）一起去逛逛，然而睡的很晚，并不知道第二天能起多早。

7月19日舟游活动 & NGNL0补票 & BML2019-VR

提前问到了酒店7点半提供早餐，就定了7点的闹钟，准时起了床。鬼知道这个晚上我睡了多久，但是活动怎么能不去呢！
和无知一起下楼拿早餐吃，酒店的工作人员大概是搞错了，给了我们两份早餐。汉庭的外包早餐是两个包子+粥+水果（香蕉）+煮整个鸡蛋，一个人吃的话实话说挺多的（flag）。

8点在商城路站见到了绿鸽鸽，然后一起去L+MALL里排队。电梯前的队伍并不算特别长，本来以为来的还算早，直到派发整理券拿到了一张427，才知道队伍到底有多长，后来才知道一天会发800张整理券。在商铺所在的楼层中，队伍里里外外围着一块空地形成环形绕了5圈，这场面引得楼上楼下的吃瓜群众纷纷围观。

在这里排队的刀客塔个个都是大佬，说话又好听，喔唷，我超喜欢在这里的。听着大佬们交流明日方舟，偶尔进去掺和几句，再打打雀，几个小时的时间就过去了。快下午1点的时候终于能进店购物了。

店不很大，所以一次也就能容纳二三十人吧，一共三个摆放明日方舟干员立牌的货架、三个明日方舟抓娃娃机（物贩期间不开放）、一个专门抽/售卖钥匙扣的柜台、四个收银位置、一个特典验证和领取柜台。给同学朋友带的东西拿完了之后，还纠结了一会给自己带一点什么，最后买了一个陈精2立牌和两个钥匙扣（陈巨帅！）。
无知花10块整了个钥匙扣，然后拎着一大袋东西走出了店，这个性价比也太高了吧。鹰角官方玩梗好评，袋子上的梗和表情包徽章都很不错，也就是我没钱整不来全套的（有钱真好）。

出店已经是中午1点多了，昨晚本来订好了今天下午BML前的游戏人生零的场次，结果因为排队排到太晚不太能赶得上。在地铁站随便买了点零食补充一点能量，然后就去梅奔楼上的SFC看游戏人生零。结果错过了开头的部分，好在不太影响整个观影体验，补票完成√。每次看NGNL0都会经历特别强烈的情感波动，这已经是第4次看了，仍然会感动到流泪，泪点太低的原因？
顺便一说，在这之后绿某人沉迷虎纹鲨鱼无法自拔，这直接导致了他的大作业……咳咳。（此处只是玩梗，绿鸽鸽怎么可能被大作业送了呢）
（这里没有图）

看完电影距离VR开场还有大约一小时，就在梅奔的-1层逛了一下，发现了中V和日V的立牌以及合作周边售卖店，不过由于来得太晚没法进去逛周边店了。由于早饭吃太多一天都没怎么感觉到饿（flag回收），随便买了点面包吃。

M晓有事溜了，围观绿鸽鸽用共享游戏电脑（奇怪的项目）打游戏，然后就要进场BMLVR了。

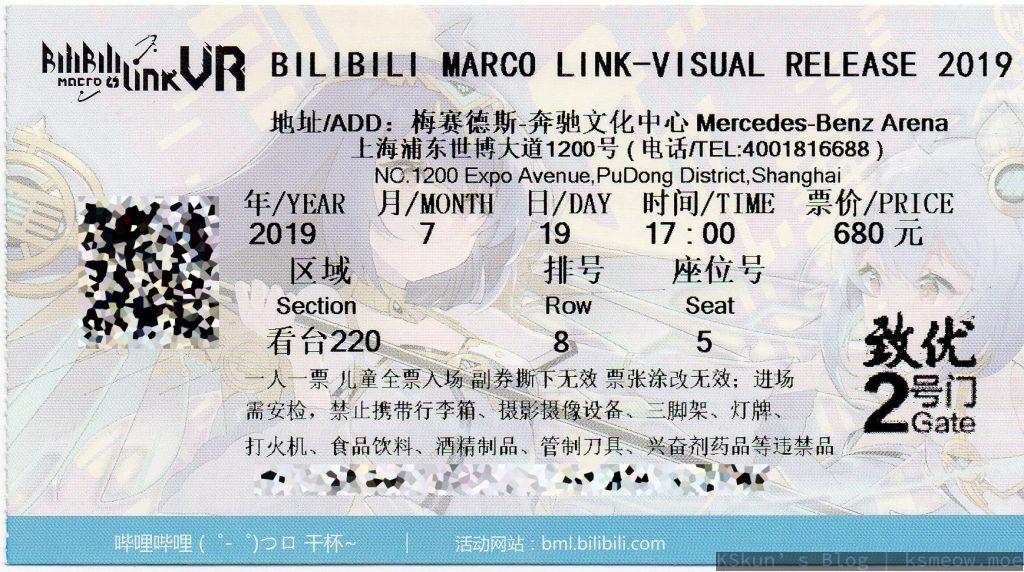
大，真的大，人生里第一次亲身来到这种规模的会场，着实把我吓了一跳。按照标志找到了座位坐下，VR的票在二层220看台，大概在环形观众席的拐角位置，离舞台相对比较远，视角依然是不错的，大约可以看清舞台上人物的动作，至于脸或者表情之类的，脑补or看屏幕转播咯。

初次参加日式live的我，心灵受到了极大的震撼。在BMLVR之前，我只是听说过有应援这回事，并不知道这是一个什么样的过程，身边有玩wota艺的朋友，但也没问过他具体的细节。
VR开场，洛天依出场，音乐响起，整个会场的气氛一瞬间就被炒热了起来。其实此时的我还是懵逼的，第一不知道如何正确地应援，第二没有荧光棒而只有赠送的发光棉棒，第三觉得无知的自己与整体的氛围格格不入。

几首歌下来，大家的热情一点都没有减少，很快就进入了中场休息。趁着休息时间我们在梅奔2层简单逛了一圈，BML周边不便宜并没舍得买（flag），看了下就溜了。门外能看到作为永久场馆保留下来的世博会中国馆。

中场休息期间还有一些问候视频播放，涉及到众多知名vtuber，DD狂喜现场。各位看客们不妨猜猜哪位的人气最高？
（以下图片仅包含部分播放了问候视频的vtuber）

上半场的一个小时里，我从一个从没有live经验的局外人逐渐变成了一个愿意参加应援的局外人，不知不觉中也拿起手中的棉棒跟着节奏挥动，尽管我还是不知道真正的应援动作。明明来之前还在担心自己一个人静静地坐在观众席上会不会过于尴尬，这算是打开了一道心锁？

下半场一开场就是vtuber一杯。第一个是小狐狸！开幕死亡 awsl

HimeHina的1 2 Fan Club，现场效果爆炸。

月ノ美兎的模型依然鬼畜，猜测是动作捕捉设备的问题。vtuber都挺喜欢玩阿伟的梗，也都在来之前很努力地学了一些中文，不过，我觉得还是说日语比较好听懂（雾）。之后是老大爱酱，不太关注爱酱所以并不知道发生了什么。

之后是B站亲女儿之一的舰B萨拉托加。但是用这样的形象唱《激昂壮志》违和感有点强，有人喊萨拉锉加233。

然后是冷鸟泠鸢，一首抒情歌曲，在今天的live里大概是一股清流。泠鸢居然虚拟up出道了？？？？？？

下半场的压轴miku！人气碾压全场，场面过于壮观，突然有点心疼其他的嘉宾。

众多日V都露了脸，简直是V厨狂欢。

甚至还有雪初音！能在VR上见到限定形象也算是赚翻了吧。

然后灯一关，开始喊安可，实际上喊的是アンコール（安口路），一开始我还没反应过来。过了一会又有人带ミク、洛天依，然后喊的内容就乱了起来。总之喊了一会就进入了返场。

进入返场着实让人眼前一亮，洛天依和miku翻唱彼此的经典歌曲（不过四秒之眷不算适合live吧），最后是同台演唱B with U，能够想象得到B站投入了多少钱……

讲真同台表演这个事情是很难想象到的吧，今年VR可以说是双厨狂喜了。最后的合唱，全场都在跟着唱。

Right here I sing a song for you
I cheer for bilibili with you
《与你同行~B with U~》

怎么说呢，对Bilibili这样一个商业网站我倒是没有什么特殊的感情，我只不过是在这个上面找点番、鬼畜之类的看，接受了它所承载的文化，不知不觉中就有了依赖感。但是我并不是一个狂热粉，并不会为了买周边而省吃饭钱，自觉自己已经半脱宅了，而且经过了一系列B站的风评事件之后也对B站没有太好的印象。然而终场的B with U却让我莫名其妙地跟其他人有了同感，大概是自己在live里确实玩的挺开心的吧。

BML2019-VR并不能算一次那么圆满的全息演唱会，过程中其实出了挺多问题的，而且有一些问题带来的影响相当严重：直播的人声听不清、声音短时中断、歌词不同步（歌词是人工操作的，估计工作人员不很了解歌曲本身）、中V粉和日V粉的奇妙关系；自己也有很多尴尬的地方：不会打call、没听说过一些嘉宾、感觉和周围的人画风格格不入。不过现场的体验质量还可以，而且并不影响我来享受live，我确实玩得挺开心，这就够了。

结束以后走出会场，拍到了世博公园的夜景，梅奔也挺漂亮的。

和无知一起去地铁站，发现地铁站的智障操作，自动售票机在闸机前面，买票的队伍直接把整个进站口拦住了，必须挤过去才能进站。好在无知有足够的硬币，买票相对快一些。

回到旅店以后跟绿鸽鸽、sak、无知、M晓四个人快乐uno。疯狂造梗：

工具人：手里很多功能牌
电话簿：手里全是数字牌
加牌传递：手里保留几张加牌功能牌，以防其他人打出加牌对自己不利

开局就全员迫害我，手牌一度高达二十几张，不过我居然是倒数第二个把牌出完的？总之就很开心。还搞了些什么galgame聊天之类的事情，一直到4点才睡。

BMLVR期间和之后发了一堆说说，空间里全是柠檬。

7月20日随便逛逛

由于前一天晚上通了个宵，中午才起了床，早饭午饭一起吃了。

然后就跑去新天地附近，在原租界找到了神奇的地方。大韩民国临时政府遗址由于中午不开放进不去，就去了一大会址。

（此处图片不便发布）

下午就去人民广场附近打街机，围观无知神仙操作。maimai这种类型的我是真不会打，巨丢人。在无知的怂恿之下我和M晓打了点太鼓，感觉更好接受一点。周围很吵，听不清乐曲节奏，就只能靠点自己熟悉的歌曲脑补出节奏来打。

回到旅店和sak、绿鸽鸽一起玩，结果变成了聚众音游。

（为了保护当事人隐私，不便发布）

无知试图在未成年人面前开车，由于车速过快被勒令停止。随后变成了开着BML主场直播的茶话会，更晚的时候sak打开了live传教，然后就又玩到了很晚。（uno真好玩）

得知崩3某活动取消补偿的消息之后，赶紧拿着我的车票申请了一发。

7月21日 BML2019-SP

由于20日又玩到很晚，21日的早上并没能起来。中午M晓去逛场贩，托他带了根棒子，然后发现只有VR的棒子还有货，不过也挺好看的。

绿鸽鸽回学校了，开场前sak惊奇地发现他的票在绿鸽鸽包里，于是使用钞能力打的去闵行取票，只能希望他好运。于是和无知、M晓一行人就无事入场去。

不愧是票最难买的一场BML，我加了钱买的B区票居然比VR的C区还后一点。开放了很多VR场未开放的区域，看上去很壮观。

开场前看到隔壁的老哥一副驾轻就熟的样子，于是搭了个话请教应援，老哥也很热心，临时帮我查了些资料。

sak遇到了堵车，并不能在开场前回来，于是在群里问第一个出场的是哪个。好巧不巧，Roselia排第一，sak惨惨。

当预告一出来全场起立欢呼打call，比VR夸张一万倍的气势，于是鼓起勇气参与了进去，模仿旁边的老哥应援。选曲、现场效果、应援热情和默契都是极好的，而且还有T台，坐在后排也有机会看清表演者的表情等，体验极佳。

真正参与进去了以后，才能体会到应援的快乐？总之就是有点累，但是开心。

sak终于在R组的最后一曲之前赶到了。

中场休息的时候和sak一起直接冲着场贩去了，想着给我校高一学弟带些礼物发下去鼓励一下，于是随便买了一些，顺便玩了一发扭蛋。有钱真好。

毕竟是来看fripSide的，Break结束后第一个就是fs，整个人都兴奋起来了。由于超炮在国内的巨高人气，fs应援气氛碾压全场。

已经无法形容这个场面有多high了，不愧是fs，现场效果炸裂。观察棒子的颜色可以看出应援棒持有率高的吓人，还好提前整了一根，不然就尴尬了。

到场的嘉宾多少都学了一些中文，勉强和观众打打招呼，有些互动。不过八叔的中文是真的不错，据说学了一年多了，还会玩梗，好评。

另外还有Aqours（颜表立，快速换色是基本操作）、eufonius（メグメル〜cuckool mix 2007〜承载着clannad的感动，虽然当时没看并不很懂）、May’n（加速世界认识的，中文好，歌也high）、SawanoHiroyuki[nZk]（泽野神曲，接触不多不过对我口味）等一众嘉宾，现场效果同样炸裂。这次作为初live质量极高，也玩得很开心。

最后的返场中，May’n和FLOW翻唱客串，全体嘉宾登台留影，离开时对着摄像机卖萌好评。