题目地址：Google Code：Dashboard – Round 2 2014 – Google Code Jam

题目描述

Aliens have landed. These aliens find our Earth’s rivers intriguing because their home planet has no flowing water at all, and now they want to construct their alien buildings in some of Earth’s rivers. You have been tasked with making sure their buildings do not obstruct the flow of these rivers too much, which would cause serious problems. In particular, you need to determine what the maximum flow that the river can sustain is, given the placement of buildings.
The aliens prefer to construct their buildings on stretches of river that are straight and have uniform width. Thus you decide to model the river as a rectangular grid, where each cell has integer coordinates (X, Y; 0 ≤ X < W and 0 ≤ Y < H). Each cell can sustain a flow of 1 unit through it, and the water can flow between edge-adjacent cells. All the cells on the south side of the river (that is with y-coordinate equal to 0) have an implicit incoming flow of 1. All buildings are rectangular and are grid-aligned. The cells that lie under a building cannot sustain any flow. Given these constraints, determine the maximum amount of flow that can reach the cells on the north side of the river (that is with y-coordinate equal to H-1).
网格图上每个格子可以流经1的流量，流量可以从相邻格子流入或流出到相邻格子。其中有一些矩形区域（互相没有公共部分）不能流。网格图的最后一行每个格子从源流入1的流量，再从网格图的第一行流出。求最大流。

输入输出格式

输入格式：
The first line of the input gives the number of test cases, T. T test cases follow. Each test case will begin with a single line containing three integers, W, the width of the river, H, the height of the river, and B, the number of buildings being placed in the river. The next B lines will each contain four integers, X0, Y0, X1, and Y1. X0, Y0 are the coordinates of the lower-left corner of the building, and X1, Y1 are the coordinates of the upper-right corner of the building. Buildings will not overlap, although two buildings can share an edge.

输出格式：
For each test case, output one line containing “Case #x: m”, where x is the test case number (starting from 1) and m is the maximum flow that can pass through the river.

输入输出样例

输入样例#1：

2
3 3 2
2 0 2 0
0 2 0 2
5 6 4
1 0 1 0
3 1 3 3
0 2 1 3
1 5 2 5

输出样例#1：

Case #1: 1
Case #2: 2

图形：
两组数据的图形分别如下。

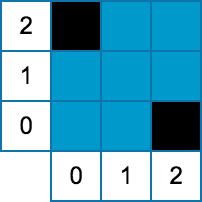
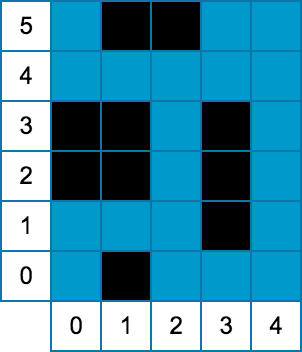
说明

1 ≤ T ≤ 100.
0 ≤ X0 ≤ X1 < W.
0 ≤ Y0 ≤ Y1 < H.
Small dataset
3 ≤ W ≤ 100.
3 ≤ H ≤ 500.
0 ≤ B ≤ 10.
Large dataset
3 ≤ W ≤ 1000.
3 ≤ H ≤ 108.
0 ≤ B ≤ 1000

题解

最大流当然可以直接建图，但是大数据的h比较大，显然直接建图跑不出。我们考虑最大流-最小割定理，将最大流转化为求最小割。由于这个图的特殊性，最小割可以看成从左侧河岸到右侧河岸的最短路。现在我们只需要套一个SPFA上去就能快速解决了。
我们接下来考虑两个矩形之间的最短路怎么计算，可以先画个图。

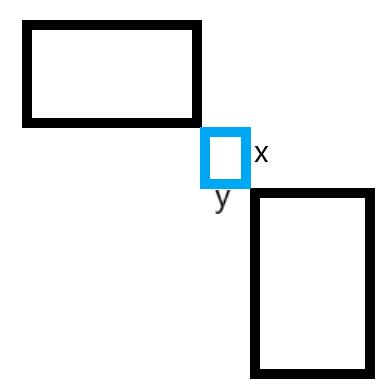
在这个图形中，这两个矩形的最短路实际上是max(x, y)。我们考虑写这样一个函数来计算最短路。

inline int caldis(int u, int v) {
    int d1 = std::max(std::max(squ[u].x1 - squ[v].x2, squ[v].x1 - squ[u].x2) - 1, 0);
    int d2 = std::max(std::max(squ[u].y1 - squ[v].y2, squ[v].y1 - squ[u].y2) - 1, 0);
    return std::max(d1, d2);
}

因为两个矩形的最短路一定是各取左下右上两个点构成图中的蓝色矩形，最短路即为蓝色矩形的长边。上述的d1和d2中的两个max是用于适配u和v矩形的位置关系的。
最好画几个图看下吧。

代码

数据下载

// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>

#include <algorithm>
#include <queue>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    register char c = fgc();
    while(c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MAXN = 1005;

struct Square {
    int x1, y1, x2, y2;
} squ[MAXN];

int T, w, h, b, dis[MAXN];

inline int caldis(int u, int v) {
    int d1 = std::max(std::max(squ[u].x1 - squ[v].x2, squ[v].x1 - squ[u].x2) - 1, 0);
    int d2 = std::max(std::max(squ[u].y1 - squ[v].y2, squ[v].y1 - squ[u].y2) - 1, 0);
    return std::max(d1, d2);
}

std::queue<int> que;
bool inque[MAXN];

inline void spfa(int s) {
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0; que.push(s); inque[s] = true;
    while(!que.empty()) {
        int u = que.front(); que.pop(); inque[u] = false;
        for(int v = 1; v <= b; v++) {
            int d = caldis(u, v);
            if(dis[v] > dis[u] + d) {
                dis[v] = dis[u] + d;
                if(!inque[v]) {
                    inque[v] = true;
                    que.push(v);
                }
            }
        }
    }
}

int main() {
    T = readint();
    for(int kase = 1; kase <= T; kase++) {
        fprintf(stderr, "Processing Case %d\n", kase);
        w = readint(); h = readint(); b = readint();
        for(int i = 1; i <= b; i++) {
            squ[i].x1 = readint(); squ[i].y1 = readint();
            squ[i].x2 = readint(); squ[i].y2 = readint();
        }
        squ[++b] = Square {-1, 0, -1, h - 1};
        squ[++b] = Square {w, 0, w, h - 1};
        spfa(b - 1);
        printf("Case #%d: %d\n", kase, dis[b]);
    }
    return 0;
}