GAMES 202 笔记:Shadow Mapping

施工中……现在没有写的部分还有:
- Convolution Soft Shadow Mapping
- Moment Shadow Mapping
- Mipmap 和 SAT 的原理
虽然没打算写,但有可能会加的部分有:
- 这几种阴影、软阴影的 GLSL 实现(看另外一个 OpenGL 渲染器的坑)
注:头图来自 GAMES 202 作业 1 任务指导书,文中部分插图来自互联网资料,引用源均在参考资料中列出。
阴影贴图(Shadow Mapping)

阴影贴图是一种 2-pass 的实时阴影渲染技术。它在阴影 pass 中以光源视角绘制阴影贴图,再在着色 pass 中利用阴影贴图的信息计算直接光照,这个过程类似将阴影生成为贴图,并应用在阴影投射到的物体(receiver)上,故如此称呼。
原始论文:Casting curved shadows on curved surfaces,发布于 SIGGRAPH 1978,作者 Lance Williams (NYIT)。
流程
判断一点是否处于阴影中,即是判断该点和光源的连线上是否存在遮挡物。这可以简单地描述为:从光源的视角能否看到遮挡物,或光源沿此方向看到物体的深度是否小于该点。要得到光源看向场景的深度信息,可以直接使用绘制场景相同的流程,而将绘制结果写入一张深度图(depth map)中即可。在计算直接光时,将该点坐标变换到光源视角中,查询深度图做比较来判断是否被遮挡。因此可以将这一过程分为两个 pass 来实现:
- 深度 pass。设置相机参数在光源处看向场景,render target 为一张深度图,并选择恰当的相机、贴图参数使场景完全包含在内。提交场景后,得到光源视角看向场景的深度信息,还需保存下此 pass 的变换参数。
- 渲染 pass。在计算光照时需要着色点的世界坐标,将其变换到光源视角中,得到深度图纹理坐标(即光源视角下 NDC 坐标系的 x、y 坐标标准化值)。使用这个坐标查询深度图,如果深度与着色点到光源距离一致说明未被遮挡,如查询深度更小说明被遮挡。
以上为基本流程,但更好的效果需要加入一些修改,详见讨论部分。
讨论
光源变换矩阵的参数
如果使用一张 2D 贴图来保存阴影信息,需要选择合适的参数。点光源应选择透视投影,而平行光源应选择正交投影,这关系到投射出阴影的形状是否正确。视锥体应该包含全部场景,远、近平面、视锥边界参数应该取得足够大,否则可能导致深度图查询越界。如果光源没有办法从一个方向看到整个场景,应该考虑生成多张不同角度的深度图,或使用 Cubemap、球形贴图等保存。
此处再整理一下流程中涉及的不同坐标系。在查询深度图时,需要将着色点的世界坐标变换到光源视角的 NDC 坐标下,这通过乘光源的视角变换和投影变换矩阵(V、P 矩阵)实现。NDC 坐标通常在 [-1, 1] 范围内(取决于 API 定义),因此还需要进一步标准化到 [0, 1] 范围,得到深度图上的纹理 UV 坐标。
自遮挡:数值误差
深度图将标准化深度值保存在贴图像素上,每个像素的颜色值是固定位数的,因此能表示的精度也是有限的,这会为数值带来量化误差。此外,深度图代表遮挡物投影至平面上的结果,但遮挡物不一定与投影平面平行,深度图上的像素实际上代表了与投影平面平行的小面元,这也会带来离散化的误差。

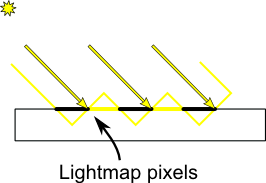
这些误差使得查询深度图的结果可能比真实遮挡物深度偏大或偏小,偏大不会造成严重后果,但偏小可能让遮挡物本身以为自己被遮挡,在没有阴影的地方形成奇怪的暗色斑点、纹路(被称为 Shadow Acne)。可以在判断被遮挡时,在着色点深度加上一个正偏差补偿数值误差,使数值误差不影响遮挡判断结果。
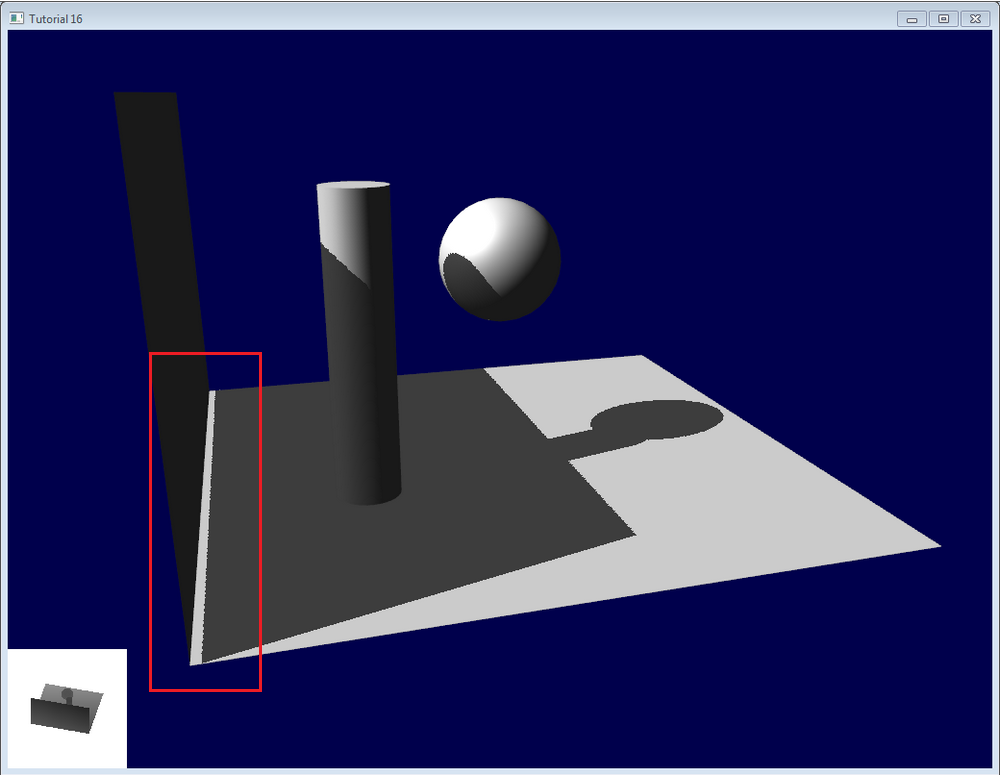
这种误差补偿是有局限性的。当遮挡平面与光源视线成较小角度时,离散化误差将变大,很难补偿这种情况的误差。而阴影遮挡物和被遮挡物离的很近时,被遮挡物的深度又被偏差补偿到小于遮挡物,使得一些阴影没有和遮挡物连起来,看起来好像遮挡物浮空了一样(被称为 Peter Panning)。可以在生成深度图时使用背面剔除,这样可以解决有厚度遮挡物的问题。
阴影的锯齿走样
由于深度图本身的尺寸有限,阴影投射后放大出现了锯齿状走样。这种走样和渲染中出现的锯齿现象原理类似,可以使用一些采样方法解决。一个方式是 PCF(百分比渐进滤波,Percentage Closer Filter)。着色点映射到深度图上后,不只查询一个像素,而是采样该像素附近一圈像素。采样的范围越大,阴影边缘的过渡部分越宽,锯齿现象越不明显,但阴影边界也会变模糊。
百分比渐进软阴影(PCSS,Percentage-Closer Soft Shadows)
Shadow Mapping 能为实时阴影计算提供遮挡信息,从而方便地实现点光源、平行光源的阴影。然而,光源常常并非二者之一,而是有一定面积的面光源。在面光源下,阴影分为本影(umbra)和半影(penumbra),本影是光源面积完全被遮挡的位置,亮度最暗,而半影是本影周围光源面积部分被遮挡的位置,形成了最暗到最亮的过渡带。半影形成的过渡带使阴影的边缘模糊,形成软阴影(soft shadow)的效果。

PCSS 受到 PCF 滤波效果的启发,通过指定阴影不同位置 PCF 滤波范围大小,来实现类似真实软阴影的效果。这种方法完全基于 Shadow Mapping 的结果,没有额外的前、后处理,也不需要更多信息。
原始论文:Percentage-Closer Soft Shadows,发布于 SIGGRAPH 2005,作者 Randima Fernando (Nvidia)。
流程
PCSS 通过控制 PCF 滤波范围大小来实现阴影不同程度的软化,因此需要确定着色点处需要选择的 PCF 滤波范围大小,这个大小与光源、遮挡物和被阴影投射物之间的集合关系决定。
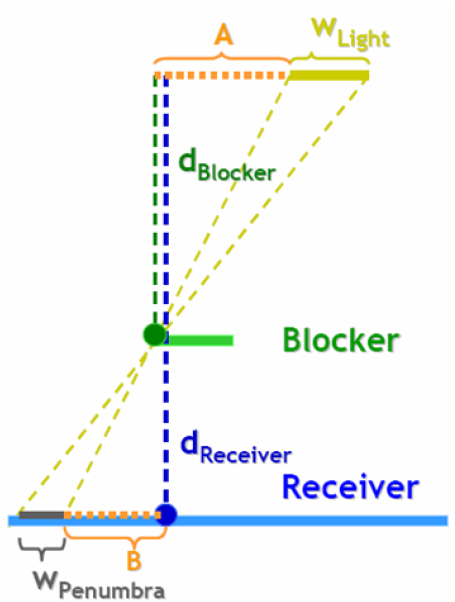
上图所示的场景中,假设光源、遮挡物和投射物平面是平行关系。黄色的线段表示有面积的光源,其宽度为 $w_\text{Light}$,光源被遮挡物(绿色线段)左侧遮挡,其阴影投射在下方的投射物(蓝色线段上),遮挡物到光源距离 $d_\text{Blocker}$,投射物到光源距离 $d_\text{Receiver}$。从光源两端点经遮挡点向投射物连线(黄色虚线),投射物两连线的右方表示两点分别无法照亮的位置,即本影,宽度为 $B$;而两连线之间的部分表示光源被部分遮挡,即半影,宽度为 $w_\text{Penumbra}$。这样就建立了阴影和场景的几何关系。注意到存在一系列相似三角形关系,存在比例
$$ \dfrac{d_\text{Blocker}}{d_\text{Receiver}-d_\text{Blocker}} = \dfrac{w_\text{Light}}{w_\text{Penumbra}} $$
故半影宽度可以由
$$ w_\text{Penumbra} = \dfrac{d_\text{Receiver}-d_\text{Blocker}}{d_\text{Blocker}} \cdot w_\text{Light} $$
求得。另外,此处的两个 $d$ 值可以不是图中的垂线段长度,满足相似三角形的比例关系皆可。
经过上面的讨论,半影宽度与光源大小、遮挡物深度和着色点深度有关,后两个量可以分别从深度图与世界坐标得到,光源大小通常是预定义好的。PCSS 的工作过程可以描述为下面三步:
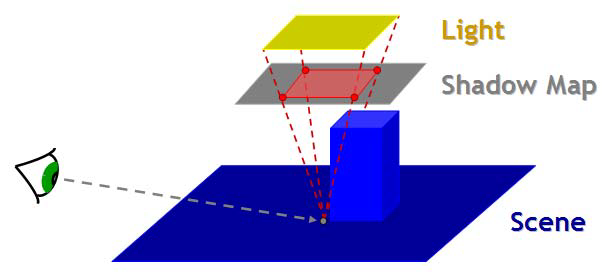
- 遮挡物搜索。由于光源有面积,能够遮挡着色点的遮挡物可能存在于一个区域中(即上图着色点和光源连线成的锥形区域),这片区域投影在深度图上也会占据一片区域。因此,要得到遮挡物的深度,需要查询所有可能遮挡到着色点的区域,求出其中遮挡物的平均深度值,这一步被称为遮挡物搜索。查询深度图的区域大小与着色点深度成正比,可定义一个比例系数作为参数。通常不会查询区域内的每个像素,而是采用采样方法估计搜索结果。
- 半影大小估计。上面的理论推导中得到了关系 $w_\text{Penumbra} = \dfrac{d_\text{Receiver}-d_\text{Blocker}}{d_\text{Blocker}} \cdot w_\text{Light}$。上一步中得到了 $d_\text{Blocker}$,而 $d_\text{Receiver}$ 可通过世界坐标中着色点到光源中心的距离估计,直接通过上面的关系计算半影大小即可。
- PCF 滤波。将半影大小作为 PCF 滤波范围大小,对深度图进行采样和滤波即可。PCF 滤波的过程可参考上文。
讨论
PCSS 是一种基于 PCF 的很直接的思路,实现的难度也不高。然而由于遮挡物搜索和 PCF 两步中包含两次采样估计过程,PCSS 的效果通常包含许多噪声,需要提高采样数或应用低通滤波等方式改善渲染质量。此外,多次采样会带来大量的贴图查询,带来时间和带宽上的额外开销,效率上依然存在问题。随着时域、空域滤波的技术发展,现在有 TAA 等更好的方法改善 PCSS 的噪声和效率,因此 PCSS 仍然是一种广泛使用的方法。
方差软阴影(VSSM,Variance Soft Shadow Mapping)
PCSS 中需要范围查询深度图中的信息来完成遮挡物搜索和 PCF,而范围查询需要通过采样来完成,这会为渲染结果带来采样造成的随机噪声。为了避免这种噪声,有许多方法通过非采样的方法来估计遮挡物的深度。VSSM 是一种利用统计规律来估计遮挡物深度的方法,它基于 Chevbyshev 不等式和方差阴影贴图(VSM,Variance Shadow Mapping)方法,通过使用预计算的信息来避免采样。
原始论文:Variance Soft Shadow Mapping,发布于 PG 2010,作者杨宝光(Autodesk、浙江大学)。
流程
在 PCSS 中,遮挡物的平均深度通过对深度图的采样获得。从这个思路出发,设采样数为 $N$,其中有 $N_1$ 个样本为非遮挡物(深度不小于着色点)、$N_2$ 个样本为遮挡物(深度小于着色点)。记遮挡物的平均深度为 $z_\text{occ}$,非遮挡物的平均深度为 $z_\text{unocc}$,所有样本的平均深度为 $z_\text{Avg}$,则根据平均值的定义可得下面的关系
$$ \dfrac{N_1}{N} z_\text{unocc} + \dfrac{N_2}{N} z_\text{occ} = z_\text{Avg} $$
采样的频率会收敛到概率,故可以用概率来估计样本的频率,此外所有样本的平均深度也可近似为真实的平均深度,则记着色点深度为 $t$,采样的随机变量取值为 $x$,上式可化为
$$ P(x \ge t) z_\text{unocc} + [1 – P(x \ge t)] z_\text{occ} = z_\text{Avg} $$
那么遮挡物的平均深度便可通过下式求出
$$ z_\text{occ} = \dfrac{z_\text{Avg} – P(x \ge t) z_\text{unocc}}{1 – P(x \ge t)} $$
有了这个关系,还需要知道非遮挡物的平均深度 $z_\text{unocc}$,以及实际意义为深度图查询范围中不小于采样点深度的像素占比 $P(x \ge t)$。
对于非遮挡物的深度,一般来说着色点附近的非遮挡物是着色点所在的平面,因此可以近似为着色点的深度 $t$。而遮挡物的占比则可以借助 VSM 的思路解决,对深度图查询范围进行采样,其对应的随机变量应是范围内像素构成的离散型随机变量,对随机变量成立单边 Chevbyshev 不等式如下(证明见附录)
$$ P(x \ge t) \le \frac{\sigma^2}{\sigma^2+(t-\mu)^2}, \forall t > \mu $$
一个会让上式的不等号取等的情况是查询范围内的深度值都一样,而实际情况中深度值常常相差不大,使用上界值估计实际情况不会有很大误差,此处取该上界的值作为 $P(x \ge t)$ 的估计。要计算这个上界,需要得到查询范围内深度的平均值 $\mu$ 和方差 $\sigma^2$,平均值可以通过 Mipmap 或 SAT 等方式得到,而方差可以通过关系 $\sigma^2 = E(x^2) – \mu^2$ 得到,因此只需要另外计算一张深度平方的深度图和它的 Mipmap/SAT 即可。
上面的理论推导得到了重要的结论,即仅需要保存深度图、深度平方图和它们的 Mipmap/SAT,就可以通过单边 Chevbyshev 不等式的上界估计平均遮挡物深度,避免了 PCSS 中遮挡物搜索的采样操作。而 PCSS 中 PCF 滤波的采样操作,则可以通过对估计出的滤波范围大小再次进行非遮挡物占比(即 $P(x \ge t)$)的估计,将其作为可见性的值,同样也可以实现无采样的滤波效果。故 VSSM 的整体流程为
- 遮挡物平均深度估计。使用与 PCSS 同样的方法得出遮挡物搜索范围的大小,在这个范围中查询 Mipmap/SAT 得到均值 $\mu$ 和平方均值 $E(x^2)$,从而计算出方差 $\sigma^2 = E(x^2) – \mu^2$,进而估计出范围内非遮挡物占比 $P(x \ge t) = \dfrac{\sigma^2}{\sigma^2+(t-\mu)^2}$,再根据 $z_\text{occ} = \dfrac{\mu – P(x \ge t) \cdot t}{1 – P(x \ge t)}$ 求出遮挡物平均深度的估计。
- 半影大小估计。这一步与 PCSS 一致。
- 可见性估计。将上一步求出的半影大小作为查询范围大小,同样地计算 $P(x \ge t)$,该值就是可见性值的估计。
讨论
VSSM 利用了单边 Chevbyshev 不等式作为平均遮挡物深度 $z_\text{occ}$ 的估计,然而不等式需要满足单边条件 $t > \mu = z_\text{Avg}$,通常在着色点附近是平面时这个条件能够被满足。当着色点附近的点和着色点不在一个平面上,尤其是远离光源方向时,实际的 $z_\text{Avg}$ 可能比着色点深度 $t$ 更大,此时使用原来的估计会使 $P(x \ge t)$ 的值小,从而使 $z_\text{occ}$ 的估计可能大于 $t$,一些本应在阴影中的像素被判断成不在阴影中,如下图所示。
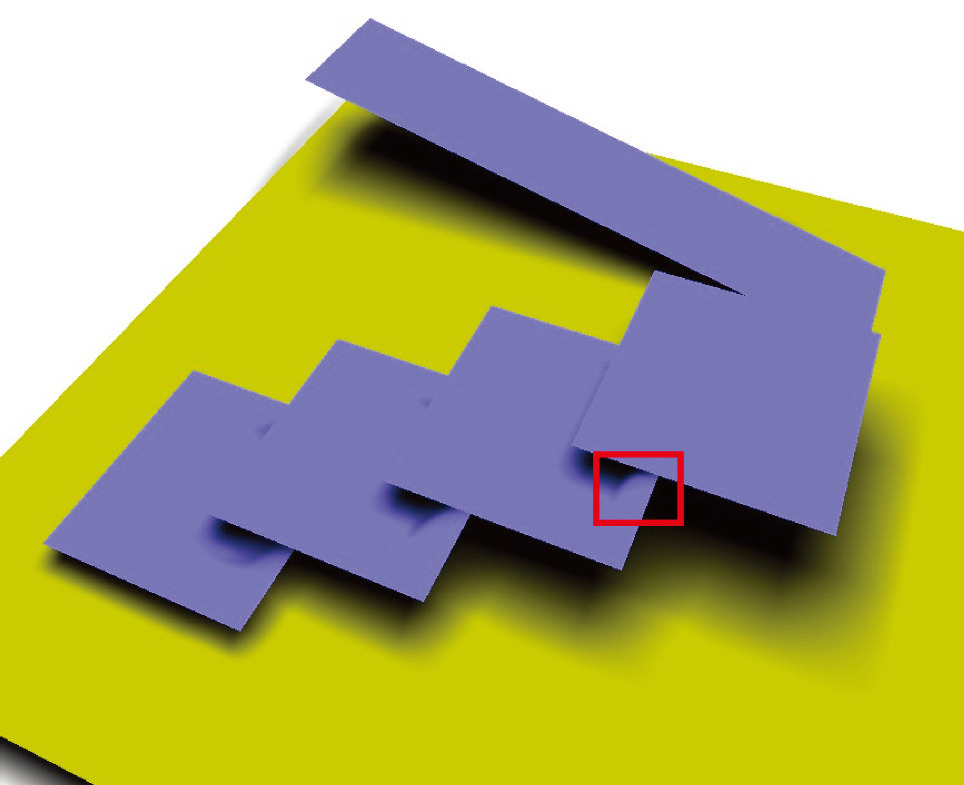
引起问题的原因是着色点附近不是平面,如果把查询范围划分成更小的格子,小格子中的几何会更接近平面,更可能满足不等式的条件。对于划分后仍然不满足条件的小格子,可以简单认为不被遮挡,或使用常规采样方法进行 PCF。
划分后,每个满足不等式条件格子 $w_{cj}$ 的 $E(x)$ 和 $E(x^2)$ 可以通过 SAT/Mipmap 直接查出,记格子的大小为 $T_{cj}$,则可以通过每个格子的信息合并得整体的 $\mu, \sigma^2$,如下所示
$$ \begin{aligned} \mu &= \dfrac{\sum_j E(x)_{cj} T_{cj}}{\sum_j T_{cj}}, \\ \sigma^2 &= \dfrac{\sum_j E(x^2)_{cj} T_{cj}}{\sum_j T_{cj}} – \mu^2 \end{aligned} $$
满足条件格子的平均遮挡物深度 $d_1$ 可以通过 $\mu, \sigma^2$ 和不等式估计得到。而不满足条件的格子则使用上文提到的采样方法,得到其平均遮挡物深度 $d_2$。根据两类格子占比对 $d_1, d_2$ 加权得到最终的平均遮挡物深度 $d$,这样一来就解决了非平面的问题。
此外,方差 $\sigma^2$ 具有的统计意义可以反映随机变量分布的集中特性,如果方差很小且 $z_\text{Avg}$ 大于着色点深度 $t$,说明着色点附近基本都是更深的点,此时可以直接认为着色点未被遮挡以减少计算。
参考资料
- GAMES 202 课件、作业指导书
- 各内容原始论文
- https://en.wikipedia.org/wiki/Shadow_mapping
- http://www.opengl-tutorial.org/cn/intermediate-tutorials/tutorial-16-shadow-mapping/
- https://github.com/TheMasonX/UnityPCSS/blob/master/Assets/PCSS/Shaders/PCSS.shader
附录
单边 Chevbyshev 不等式的证明
参考资料:https://zhuanlan.zhihu.com/p/111329527
Markov 不等式
设 $X$ 是取非负值的随机变量,则对于任何常数 $a>0$,有
$$ P(X \ge a) \le \frac{E(X)}{a} $$
证明 对于 $a>0$ 令随机变量 $I = \begin{cases} 1, & X \le a \\ 0, & X < a \end{cases}$,由于 $X>0$ 有 $I \le \dfrac{X}{a}$,两边求期望得 $E(I) = P(X \ge a) \le \dfrac{E(X)}{a}$。
单边 Chevbyshev 不等式
设 $X$ 具有 0 均值和有限方差 $\sigma^2$,则对任意 $a>0$ 有
$$ P(X \ge a) \le \frac{\sigma^2}{\sigma^2+a^2} $$
证明 引入常数 $b>0$,则有 $X \ge a \Rightarrow X+b \ge a+b \Rightarrow (X+b)^2 \ge (a+b)^2$,因此有
$$ P(X \ge a) = P(X+b \ge a+b) \le P[(X+b)^2 \ge (a+b)^2] $$
由 Markov 不等式可进一步推得
$$ P(X \ge a) \ge P[(X+b)^2 \ge (a+b)^2] \le \frac{E[(X+b)^2]}{(a+b)^2} = \frac{\sigma^2+b^2}{(a+b)^2} $$
既然上式对任意常数 $b>0$ 都成立,取右式关于 $b$ 的极小值时 $b = \dfrac{\sigma^2}{a}$,得到
$$ P(X \ge a) \le \frac{\sigma^2}{\sigma^2+a^2} $$
推论 设 $X$ 均值为 $\mu$,则上述结论式可变为对任意 $a>\mu$ 有
$$ P(X \ge a) \le \frac{\sigma^2}{\sigma^2+(a-\mu)^2} $$
取等条件 其中一个充分条件为 $P(X=0)=1$。
