注：本文部分图片来自互联网，其相关权利归原作者所有，感谢原作者的分享。

概述

左偏树是一种可并堆的类型，它能够实现插入、删除、合并O(\log n)的功能。这里介绍它的原理和实现。

原理

结构

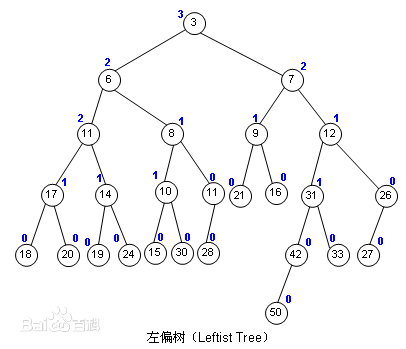
上图为一个左偏树的示意图。
我们给出一些定义。定义一个点的距离为总是从右子树走到达一个没有右儿子的点的距离。可以发现，所谓左偏，就是指左儿子的距离不小于右儿子的距离，这种性质被称为左偏性。
左偏树同时也要满足堆序性，对于小根堆，堆序性指的是对于每个点，值总比它的儿子小。
可以观察到，上图中的左偏树满足以上性质。

合并

左偏树的精髓即为合并操作。要实现O(\log n)的合并操作，我们首先得探究几个性质。
性质 一个点的距离等于右儿子的距离+1。
性质 一个点的左子树和右子树都是左偏树。
以小根堆的合并为例，首先，我们将根较小的一棵树作为基础，取它的右子树跟另外一棵树合并。合并完毕的树的根的距离可能改变，此时如果不满足左偏性需要调换左右子树。此外，还要更新现在根的距离。递归合并即可。

插入

即为一个单点左偏树和一个左偏树合并，直接合并即可。

删除根

重置左右儿子的父亲并且合并左右子树即可。

构造

一种方法是一个一个地插入。
考虑使用队列优化这种构造。从队列中取出2个元素，合并后插入队尾，以此类推，这种构造可以做到O(n)。

删除任意

在堆中，没有快速查找某值的位置的方法，但是如果我们知道了一个位置，我们还是可以考虑删除该位置上的点。先合并左右子树，把合并后的左偏树挂到这个点上。这可能会导致这个点父亲不满足左偏性，因此要从这个点到根一层层检查交换左右子树。

例子

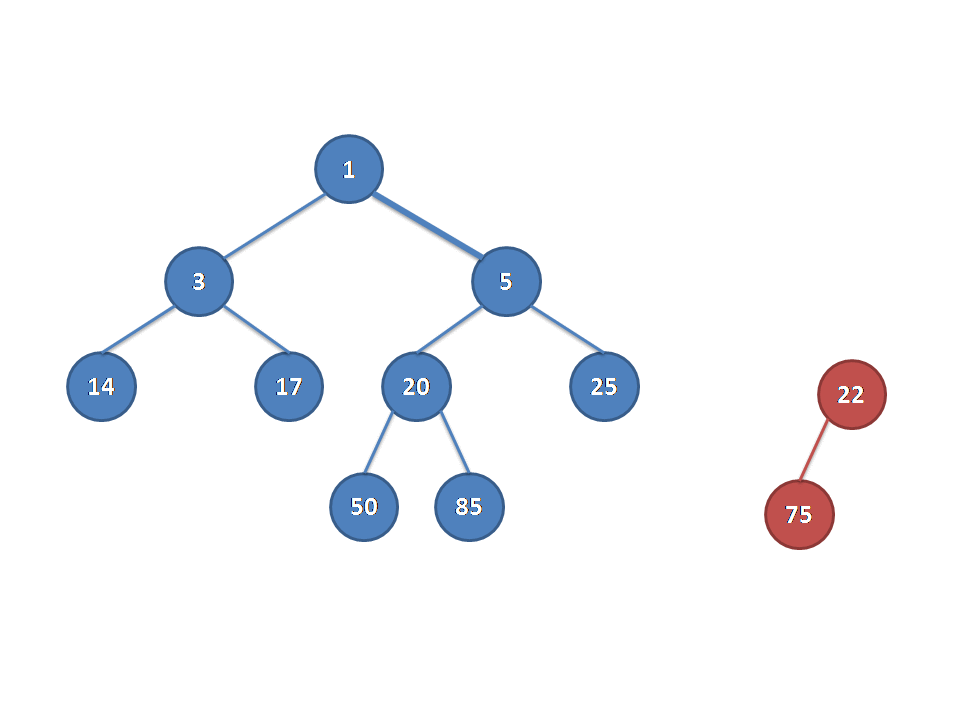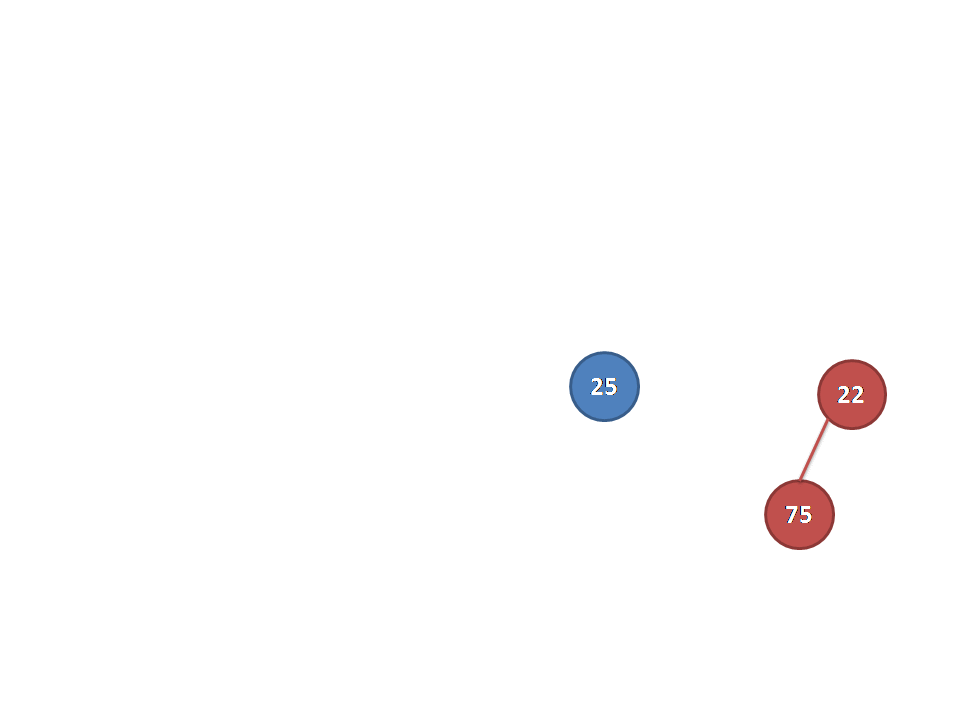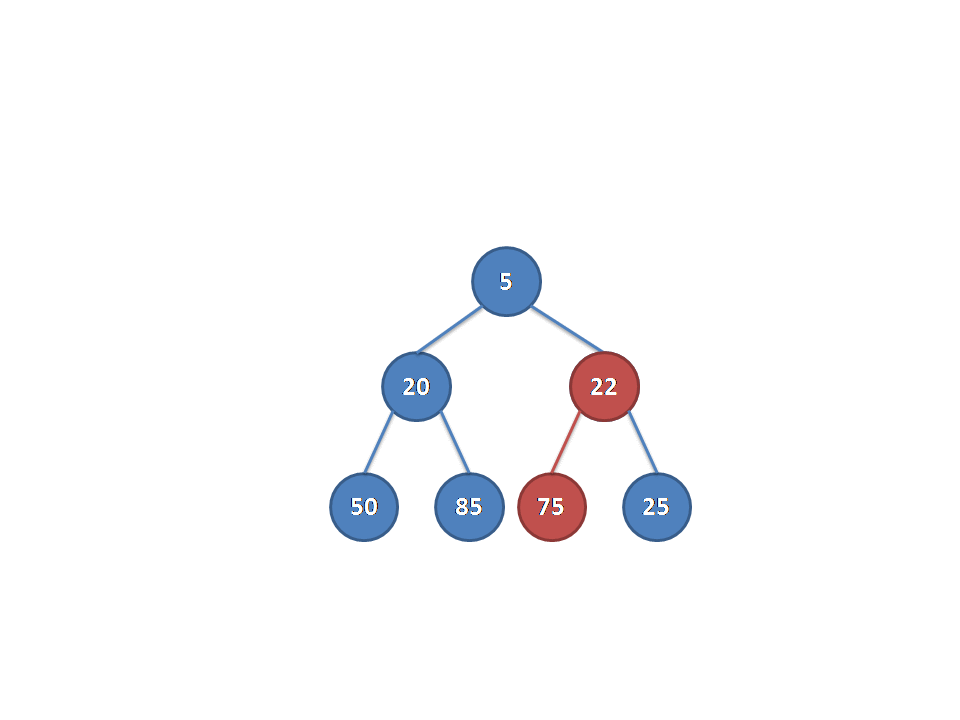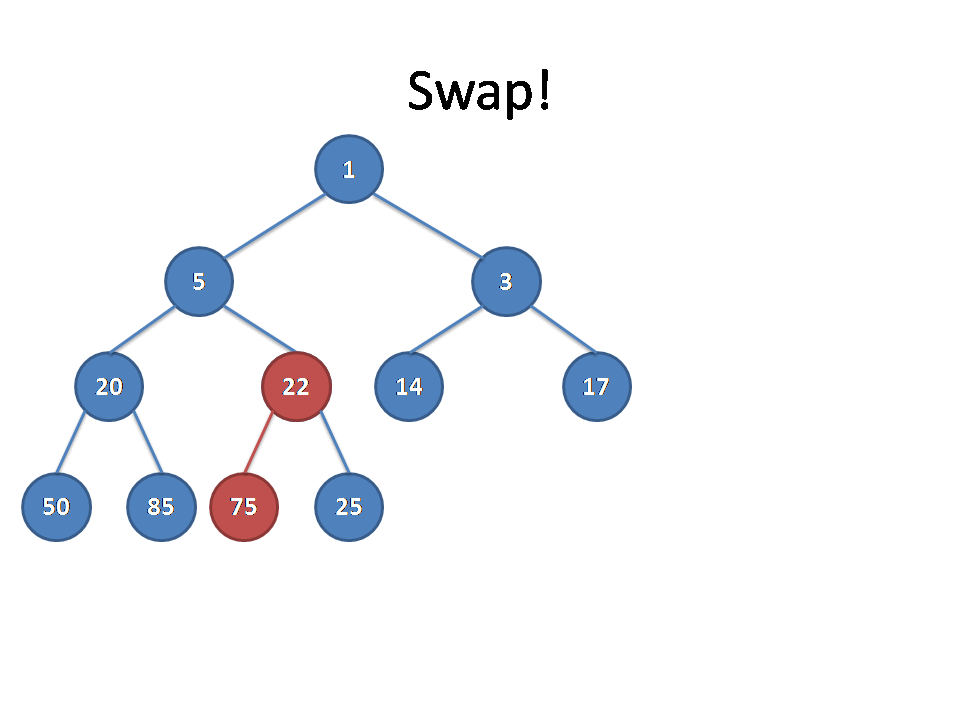
下图展示了一个左偏树合并的过程。图片来自远航之曲博客。

实现

准备工作

我们需要用四个数组构建一棵左偏树。val数组为节点值，fa数组为父亲节点，ch为子节点，dis为该点的距离。距离的定义见上。

合并

需要讨论两棵树存在一棵为空的情况，如果为空返回另一棵。

inline int merge(int x, int y) {
    if(x == 0) return y;
    if(y == 0) return x;
    if(val[x] > val[y]) std::swap(x, y);
    ch[x][1] = merge(ch[x][1], y);
    fa[ch[x][1]] = x;
    if(dis[ch[x][0]] < dis[ch[x][1]]) std::swap(ch[x][0], ch[x][1]);
    dis[x] = dis[ch[x][1]] + 1;
    return x;
}

删除树根

inline void delroot(int x) {
    val[x] = -1;
    fa[ch[x][0]] = fa[ch[x][1]] = 0;
    merge(ch[x][0], ch[x][1]);
}

删除任意

inline void delet(int x) {
    int p = merge(ch[x][0], ch[x][1]);
    fa[p] = fa[x];
    val[x] = -1;
    for(int i = fa[x]; i; i = fa[i]) {
        if(dis[ch[i][0]] < dis[ch[i][1]]) std::swap(ch[i][0], ch[i][1]);
        if(dis[i] == dis[ch[i][1]] + 1) return;
        dis[i] = dis[ch[i][1]] + 1;
    }
}

一道例题：【模板】左偏树（可并堆）

题意

有两种操作：①合并两个小根堆；②查询、删除堆的最小数。

题解

左偏树，支持合并、查所在树以及删除根即可。

代码

// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>

struct io {
    char buf[1 << 26], *op;
    io() {
        fread(op = buf, 1, 1 << 26, stdin);
    }
    inline int readint() {
        register int res = 0, neg = 1;
        while(*op < '0' || *op > '9') if(*op++ == '-') neg = -1;
        while(*op >= '0' && *op <= '9') res = res * 10 + *op++ - '0';
        return res * neg;
    }
    inline char readchar() {
        return *op++;
    }
} ip;

#define readint ip.readint
#define readchar ip.readchar

// Leftist Tree

int fa[100005], val[100005], dis[100005], ch[100005][2];

inline int getroot(int x) {
    while(fa[x]) x = fa[x];
    return x;
}

inline int merge(int x, int y) {
    if(x == 0) return y;
    if(y == 0) return x;
    if(val[x] > val[y] || (val[x] == val[y] && x > y)) std::swap(x, y);
    ch[x][1] = merge(ch[x][1], y);
    fa[ch[x][1]] = x;
    if(dis[ch[x][0]] < dis[ch[x][1]]) std::swap(ch[x][0], ch[x][1]);
    dis[x] = dis[ch[x][1]] + 1;
    return x;
}

inline void poproot(int x) {
    val[x] = -1;
    fa[ch[x][0]] = fa[ch[x][1]] = 0;
    merge(ch[x][0], ch[x][1]);
}

int n, m, op, x, y;

int main() {
    n = readint();
    m = readint();
    dis[0] = -1;
    for(int i = 1; i <= n; i++) {
        val[i] = readint();
    }
    for(int i = 1; i <= m; i++) {
        op = readint();
        if(op == 1) {
            x = readint();
            y = readint();
            if(val[x] == -1 || val[y] == -1 || x == y) continue;
            x = getroot(x);
            y = getroot(y);
            merge(x, y);
        } else {
            x = readint();
            if(val[x] == -1) {
                printf("-1\n");
                continue;
            }
            x = getroot(x);
            printf("%d\n", val[x]);
            poproot(x);
        }
    }
    return 0;
}

参考资料

• 左偏树的特点及其应用(转) – CSDN博客
• 左偏树学习总结 | 远航休息栈