Link-Cut Tree(动态树)原理与实现

概述
LCT是一种实用数据结构(?),它滋磁维护树上信息,而且这个树是可以变换结构的。具体而言,它维护了一个Splay森林,利用Splay的功能可以维护树上信息,且可以对树结构进行拆分、连接等操作。下面介绍LCT的原理与实现。
原理与实现
一些定义
辅助树(auxiliary tree):在LCT中,用于维护重链信息的Splay。其维护的有序性以深度为参数,即其中序遍历为该链从根到重儿子的顺序。
访问(access):从树根出发,将根到某个节点的路径设置为重链。
重儿子(偏好儿子,preferred child):访问到的树链的最底层节点。
重边(偏好边,preferred edge):重链中,指向重儿子方向的边。
重链(偏好链,preferred path):访问时走过的路径,由重边和重儿子组成。
所有的访问都会创造出重链,但是由于LCT的操作,重链可能会断掉。具体的操作需要等到讲到操作的时候才能够说清楚。
注意,辅助树是为了便于维护树上信息,其形态不一定与原树相同,我们后面会讲到辅助树与原树的关系。
树的结构
刚刚也说到了,实际上LCT维护的是一个Splay森林。一棵Splay维护的是一条重链的信息。下面是一个LCT的示意图。
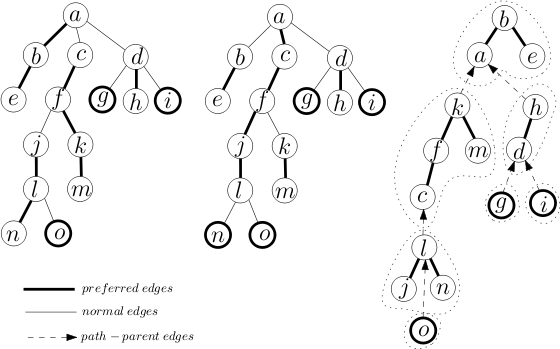
图片来自Wikipedia:Link/cut tree – Wikipedia。
图片中,粗边即为重边,而细边我们将它定义为轻边。左→中表示的是以a为根的有根树访问l节点所造成的变化。右图展示的是Splay的划分。
我们说,Splay维护的是重链信息,而当前Splay和原树中重链顶的父节点通过轻边(右图虚线箭头)来连接。
从现在开始,文章内容默认你已经会使用Splay的操作。如果Splay仍不会,可以参考Splay原理与实现 | KSkun’s Blog一文。
LCT的核心:访问(access)
访问,即从树根出发,将树根到某节点x的路径设置为重链的操作。要实现这个操作,我们需要将这一排点加入到一个Splay中。
实现上,我们要断掉链上的点与之前重儿子的连接,将其合并到一个Splay中。我们从重儿子x向树根处理,每次将节点splay到所在辅助树的根,此时该点的右子树为以前重链上需要切掉的一段。切断这条重边,并将右儿子的连边设置为向当前重儿子的重边即可。
实现上,我们统一用fa这一变量来存储父亲的信息,也就是说这个fa可能指的并非所在Splay的父节点,而是轻边的父节点。但是每个节点的儿子信息则完全是Splay中的儿子信息,即轻边的儿子不会在父节点有记录。因此我们只需更改每个节点的右儿子即可,并不需要重置右儿子的父亲信息。
inline void access(int p) {
for(int q = 0; p; q = p, p = tr[p].fa) {
splay(p);
tr[p].ch[1] = q;
update(p);
}
}
换根(make_root)
换根,即将原树转换为以某节点x为树根的有根树。
我们可以访问该节点,并将其splay至根。由于Splay内部的有序以深度为依据,x只有左儿子,此时表示x在重链的底端。我们对这棵Splay进行翻转,x就变为重链的顶端,即原树树根。
inline void makert(int p) {
access(p);
splay(p);
reverse(p);
}
找根(find_root)
找根,即找到某节点x所在原树的树根。
先访问该节点,splay至根。此时这条链上深度最小的点即为原树树根。因此我们只需找到最左的左儿子即可。
inline int findrt(int p) {
access(p);
splay(p);
while(tr[p].ch[0]) p = tr[p].ch[0];
return p;
}
分离树链(split)
分离树链,即将原树中某节点u到v的路径分离出来。
我们考虑将链的一端u设为树根,并访问v,将v splay到根。此时对于这条树链,在u、v所在的Splay上的体现即为v及v的左子树。
inline void split(int u, int v) {
makert(u);
access(v);
splay(v);
}
连接原树(link)
连接原树,即将某节点u、v所在的原树通过边(u, v)连接起来。
先将其中一点u设为原树根,以轻边接到v上即可。如果此处利用split,效果其实是一样的。
inline void link(int u, int v) {
split(u, v);
tr[u].fa = v;
}
切断原树(cut)
切断原树,即将本相连的节点u、v之间的边切断。
先将这条边split出来,然后切断父子关系即可。如果左儿子不是u或者左儿子有右儿子,那么表示不存在(u, v)这条边。
inline void cut(int u, int v) {
split(u, v);
if(tr[v].ch[0] != u || tr[tr[v].ch[0]].ch[1]) return;
tr[u].fa = tr[v].ch[0] = 0;
}
改变点值(modify)
你需要把该点提至整棵树的树根,再做修改,这样可以避免修改后还要向上更新根的信息。
inline void modify(int u, int w) {
access(u);
splay(u);
tr[u].val = w; // 更改值
update(u);
}
与单独Splay操作的区别
由于我们用fa混着存两种边关系,即轻儿子、重儿子,我们不好判断Splay根的位置。下面是一种判断是否为Splay根的方法。
inline bool isroot(int p) {
int fa = tr[p].fa;
return tr[fa].ch[0] != p && tr[fa].ch[1] != p;
}
对于Splay中常见的旋转(rotate)、伸展(splay)操作,实现上有些许区别。主要原因判断Splay根的方式变了。
inline void rotate(int p) {
bool t = !isleft(p); int fa = tr[p].fa, ffa = tr[fa].fa;
tr[p].fa = ffa; if(!isroot(fa)) tr[ffa].ch[!isleft(fa)] = p;
tr[fa].ch[t] = tr[p].ch[!t]; tr[tr[fa].ch[t]].fa = fa;
tr[p].ch[!t] = fa; tr[fa].fa = p;
update(fa);
}
inline void splay(int p) {
pushto(p);
for(int fa = tr[p].fa; !isroot(p); rotate(p), fa = tr[p].fa) {
if(!isroot(fa)) rotate(isleft(fa) == isleft(p) ? fa : p);
}
update(p); // 对p只update一次,优化常数
}
辅助树与原树的关系
原树在LCT中其实是剖成几条树链的,每条树链一个Splay。原树的结构中树链顺序,则为Splay的顺序,父子关系也依赖着轻重边来进行管理。但是LCT这个奇妙的Splay森林结构并不和原来的有根树完全相同,Splay根和树根也并不相同。
最开始看LCT就是在这里搞不懂的。而且直到现在我也不知道应该怎么写这段内容GG。
例题:【P3690】【模板】Link Cut Tree (动态树) – 洛谷
题目描述
- 求链点权异或和
- 连接树边
- 断开树边
- 改变点权
题解
我们在节点处维护一个子树异或和(Splay意义上的子树),每次查询split以后查。
修改操作则先访问它并且把这个点splay到根再改。
代码
// Code by KSkun, 2018/4
#include <cstdio>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 300005;
struct Node {
int ch[2], fa, val, xsum;
bool rev;
} tr[MAXN];
inline bool isleft(int p) {
return tr[tr[p].fa].ch[0] == p;
}
inline bool isroot(int p) {
return tr[tr[p].fa].ch[0] != p && tr[tr[p].fa].ch[1] != p;
}
inline void update(int p) {
tr[p].xsum = tr[p].val ^ tr[tr[p].ch[0]].xsum ^ tr[tr[p].ch[1]].xsum;
}
inline void reverse(int p) {
std::swap(tr[p].ch[0], tr[p].ch[1]);
tr[p].rev ^= 1;
}
inline void pushdown(int p) {
if(tr[p].rev) {
if(tr[p].ch[0]) reverse(tr[p].ch[0]);
if(tr[p].ch[1]) reverse(tr[p].ch[1]);
tr[p].rev ^= 1;
}
}
int sta[MAXN], stop;
inline void pushto(int p) {
stop = 0;
while(!isroot(p)) {
sta[stop++] = p;
p = tr[p].fa;
}
sta[stop++] = p;
while(stop) {
pushdown(sta[--stop]);
}
}
inline void rotate(int p) {
bool t = !isleft(p); int fa = tr[p].fa, ffa = tr[fa].fa;
tr[p].fa = ffa; if(!isroot(fa)) tr[ffa].ch[!isleft(fa)] = p;
tr[fa].ch[t] = tr[p].ch[!t]; tr[tr[fa].ch[t]].fa = fa;
tr[p].ch[!t] = fa; tr[fa].fa = p;
update(fa);
}
inline void splay(int p) {
pushto(p);
for(int fa = tr[p].fa; !isroot(p); rotate(p), fa = tr[p].fa) {
if(!isroot(fa)) rotate(isleft(fa) == isleft(p) ? fa : p);
}
update(p);
}
inline void access(int p) {
for(int q = 0; p; q = p, p = tr[p].fa) {
splay(p);
tr[p].ch[1] = q;
update(p);
}
}
inline void makert(int p) {
access(p);
splay(p);
reverse(p);
}
inline int findrt(int p) {
access(p);
splay(p);
while(tr[p].ch[0]) p = tr[p].ch[0];
return p;
}
inline void split(int u, int v) {
makert(u);
access(v);
splay(v);
}
inline void link(int u, int v) {
split(u, v);
tr[u].fa = v;
}
inline void cut(int u, int v) {
split(u, v);
if(tr[v].ch[0] != u || tr[u].ch[1]) return;
tr[u].fa = tr[v].ch[0] = 0;
}
inline void modify(int u, int w) {
access(u);
splay(u);
tr[u].val = w;
update(u);
}
int n, m, op, x, y;
int main() {
n = readint(); m = readint();
for(int i = 1; i <= n; i++) {
tr[i].val = tr[i].xsum = readint();
}
while(m--) {
op = readint(); x = readint(); y = readint();
switch(op) {
case 0:
split(x, y);
printf("%d\n", tr[y].xsum);
break;
case 1:
link(x, y);
break;
case 2:
cut(x, y);
break;
case 3:
modify(x, y);
}
}
return 0;
}
