归并排序

归并排序是O(nlogn)排序算法（归并、快排、堆排）中最有分治特点的一个。它的核心正如其名“归并”，也就是分治解决子问题并合并子问题。

分析

谈到分治，我们可以对这个问题进行划分：

主问题：使一堆无序的数字变得有序；
子问题：二分数字，使两边分别变得有序；
合并子问题：见下分析。

如何将2个有序的数列合并成1个有序的数列呢？这个时候我们可以把两个数列并排着放，使他们的小端对齐。定义两个指针分别指向两个小端，如下图^[3]。

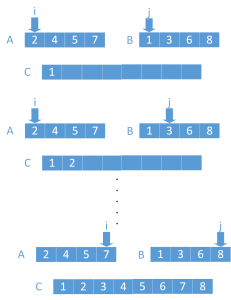
首先我们可以确定的是，两堆数的最小值肯定是两堆数小端的其中一个数，既然如此，我们比较两个小端数并取出最小的。利用上面得到的结论可以推演，每次从小端取最小数，取完为止，这样得到的数列一定是升序的。这样我们就完成了合并子问题的设计。

代码

int arr[1005], tmp[1005];

void msort(int l, int r) {
    if(l == r) return;
    int m = (l + r) >> 1;
    msort(l, m);
    msort(m + 1, r);
    int i = l, j = m + 1, k = l; // i, j管理arr, k管理tmp
    while(i <= m && j <= r) { if(arr[i] > arr[j]) {
            tmp[k++] = arr[j++]; // 小的在前 
        } else {
            tmp[k++] = arr[i++];
        }
    } 
    // 处理两部分长度不等的情况 
    while(i <= m) {
        tmp[k++] = arr[i++];
    }
    while(j <= r) {
        tmp[k++] = arr[j++];
    }
    for(int i = l; i <= r; i++) {
        arr[i] = tmp[i];
    }
}

逆序对问题 洛谷P1908

这个问题是这样的：我们有一个数列a₁, a₂, …, a_n，现在我们规定满足条件i < j且a_i > a_j的数对(a_i, a_j)为该数列的一个逆序对。给定数列{a_n}，求数列中所有的逆序对数。

分析

这个问题的解决方法有很多，但是我们可以参考归并排序的设计方法，也设计分治的结构：

主问题：得到数列中逆序对的数量
子问题：二分，得到两边各有多少逆序对
合并问题：两边逆序对数加起来并找出跨两边的逆序对数量

好了，现在还剩下的问题是怎么找出跨两边的逆序对数量。我们想起了归并排序两个有序数列的选择方式。如果我们把左边右边并排放，选小端，左边的小端数大于右边的小端数，这意味着右边的小端数与左边小端数和左边比小端数大的那些数都可构成逆序对，这就可以统计跨越两边的逆序对。仔细分析，我们发现右边的每一个数都会只被这样统计一遍，因此不会计重解或漏解。算法的正确性得证。

代码

#include <cstdio>

int arr[40005], tmp[40005];

int msort(int l, int r) {
    int cnt = 0;
    if(l == r) return 0;
    int m = (l + r) >> 1;
    cnt += msort(l, m);
    cnt += msort(m + 1, r);
    int i = l, j = m + 1, k = l; // i, j管理arr, k管理tmp
    while(i <= m && j <= r) { if(arr[i] > arr[j]) {
            tmp[k++] = arr[j++]; // 小的在前 
            cnt += m - i + 1;
        } else {
            tmp[k++] = arr[i++];
        }
    } 
    // 处理两部分长度不等的情况 
    while(i <= m) {
        tmp[k++] = arr[i++];
    }
    while(j <= r) {
        tmp[k++] = arr[j++];
    }
    for(int i = l; i <= r; i++) {
        arr[i] = tmp[i];
    }
    return cnt;
}

int n;

int main() {
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        scanf("%d", &arr[i]);
    }
    printf("%d ", msort(0, n - 1));
    return 0;
}

以上代码已通过洛谷P1908评测。

参考资料

1. 白话经典算法系列之五 归并排序的实现 – MoreWindows Blog – CSDN博客
2. 归并排序求逆序对 – ACdreamer – CSDN博客
3. 二路归并排序 – horizon.qiang – 博客园