フロム/TRUE 日中罗马音歌词
フロム 作词:唐沢美帆 作曲:南田健吾 / h-wonder 歌:TRUE(唐沢美帆) 下 …
May all the beauty be blessed.
作词:志倉千代丸、江幡育子
作曲:志倉千代丸、磯江俊道
歌:彩音
歌词来源:いつもこの場所で(剧场版《命运石之门 负荷领域的既视感》主题曲 / 劇場版「STEINS) – 彩音 – 单曲 – 网易云音乐
翻译来源:いつもこの場所で(剧场版《命运石之门 负荷领域的既视感》主题曲 / 劇場版「STEINS) – 彩音 – 单曲 – 网易云音乐
翻译作者:谎言-葬仪-死去 – 用户 – 网易云音乐
信息来源:いつもこの場所で | Bangumi 番组计划
罗马音来源:自制 航空母艦飛龍 – 用户 – 网易云音乐
协力:Google 翻译
いつか僕らが 未来 振り返る時には
Itsuka bokura ga mirai furikaeru tokiniwa
何时我们回顾未来的时候
いつもこの場所で キミが笑って
Itsumo kono basho de kimi ga waratte
你总在此处微笑
残酷に過ぎ行く 時の中で
Zankoku ni sugiyuku toki no naka de
探求的事物
探し求めていたもの
Sagashi motomete ita mono
随着时间残酷地流逝
すれ違う世界に 閉じ込められた
Surechigau sekai ni toji komerareta
微弱的光芒
目に見えぬヒカリ
Me ni mienu Hikari
被关在擦身而过的世界里
特別なほど 愛する者へ
Tokubetsuna hodo aisuru mono e
隐瞒着
打ち明けられずにいた
Uchiake rarezu ni ita
特别而心爱的人
過ごした日々の 一つ一つが
Sugoshita hibi no hitotsu hitotsu ga
解开过去日子中
戸惑いをピリオドに変える
Tomadoi o piriodo ni kaeru
一个个的困惑
いつか僕らが 未来 振り返る時には
Itsuka bokura ga mirai furikaeru tokiniwa
何时我们回顾未来的时候
いつもこの場所で キミが笑って
Itsumo kono basho de kimi ga waratte
你总在此处微笑
重ね合った みんなの想いが
Kasaneatta min’na no omoi ga
大家的思念交织重叠
世界線を創る
Sekai-sen o tsukuru
将世界线创造
どんな雨にも 負けぬ
Don’na ame ni mo makenu
无论怎样的风雨 我们都不认输
信じ合える気持ち
Shinjiaeru kimochi
互相信任的心情
この空の観測者
Kono sora no kansoku-sha
这片天空的观测者
この空は明日の証明
Kono sora wa asu no shōmei
这片天空是明天的证明
いつまでも変わらぬ
Itsu made mo kawaranu
永远不会改变的景色
景色なんて 絶対に叶わぬ夢
Keshiki nante zettai ni kanawanu yume
绝对无法实现的梦想
奇跡のような出会い
Kiseki no yōna deai
奇迹般的邂逅
せめてあの日を 消したりしないで
Semete ano hi o keshi tari shinaide
至少想要留住那一天
好きな気持ちが 勇気に変わる
Sukina kimochi ga yūki ni kawaru
喜欢你的心情化成了勇气
科学的じゃないけど
Kagaku-teki janaikedo
虽然这不科学
戸惑いのない キミの言葉が
Tomadoi no nai kimi no kotoba ga
不要不知所措
本当の答えを導く
Hontō no kotae o michibiku
你的话语指引着真正的答案
あの日僕らは 出会い 大切な何かを
Anohi bokurawa deai taisetsuna nanika o
那一天 我们有什么重要的东西相遇了
いつもこの場所で 探していたね
Itsumo kono basho de sagashite ita ne
曾经总是在此处寻找
何気なく 過ぎゆく時間の
Nanigenaku sugi yuku jikan no
无意间 在流逝的时间中
その意味を知ってる
Sono imi o shitteru
明白了这其中的意义
たとえどんなに 二人 離れてしまっても
Tatoe don’nani futari hanarete shimatte mo
即使两人分隔两地
この空の観測者 この空は明日の証明
Kono sora no kansoku-sha kono sora wa asu no shōmei
这片天空的观测者,这片天空是明天的证明
たとえ僕らは 遠く 離れてしまっても
Tatoe bokura wa tōku hanarete shimatte mo
无论我们分隔多远
いつもこの場所で 繋がっている
Itsumo kono basho de tsunagatte iru
总是在此处相连
切なくてロマンチックだね
Setsunakute romanchikkuda ne
悲伤而又浪漫
まだ知らない明日
Mada shiranai ashita
未知的明天
いつか僕らが 未来 振り返る時には
Itsuka bokura ga mirai furikaeru tokiniwa
何时我们回顾未来的时候
いつもこの場所で キミが笑って
Itsumo kono basho de kimi ga waratte
你总在此处微笑
重ね合った みんなの想いが 世界線を創る
Kasaneatta min’na no omoi ga sekai-sen o tsukuru
大家的思念交织重叠,将世界线创造
どんな雨にも 負けぬ 信じ合える気持ち
Don’na ame ni mo makenu shinjiaeru kimochi
无论怎样的风雨 我们都不认输 互相信任的心情
この空の観測者 この空は明日の証明
Kono sora no kansoku-sha kono sora wa asu no shōmei
这片天空的观测者,这片天空是明天的证明
一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(假设出发时油箱是空的)。给定两个城市之间的距离D1、汽车油箱的容量C(以升为单位)、每升汽油能行驶的距离D2、出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di、每升汽油价格Pi(i=1,2,…,N)。计算结果四舍五入至小数点后两位。如果无法到达目的地,则输出“No Solution”。
第一行,D1,C,D2,P,N。
接下来有N行。
第i+1行,两个数字,油站i离出发点的距离Di和每升汽油价格Pi。
所需最小费用,计算结果四舍五入至小数点后两位。如果无法到达目的地,则输出“No Solution”。
275.6 11.9 27.4 2.8 2 102.0 2.9 220.0 2.2
26.95
N≤6,其余数字≤500
这题我采取的方法是模拟车在加油站之间行驶的过程,使过程中需要用的每一份油都使用能够使用的最便宜的油。这种想法比较抽象,难以理解,不过清晰并且实现起来容易。题解中会有分析和举例帮助理解。
首先说一下怎么做到“使过程中需要用的每一份油都使用能够使用的最便宜的油”。我们不断地维护可用的“燃油提供者”(即加油站)的列表。等到要用油的时候,再从列表中选取最便宜的油拿来用,而不是在到那个油站的时候就决定好加多少油。我们设想现在正打算从加油站G1行驶到G2,模拟选取最优的过程。这个过程需要讨论,细节如下:
可以容易得出以下的结论:
需要讨论的内容:
以题目样例为例:

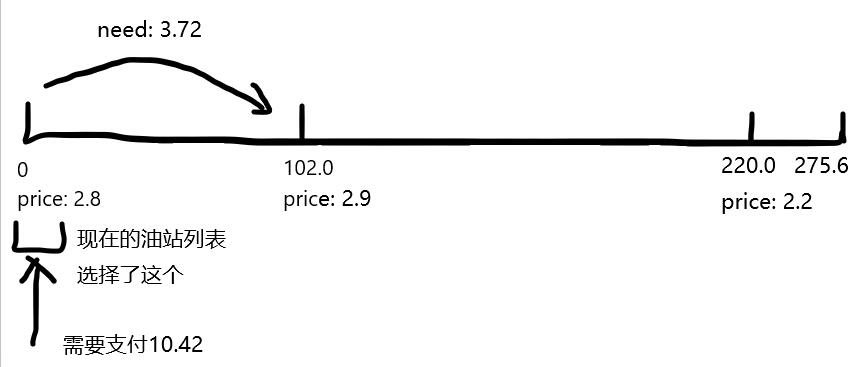
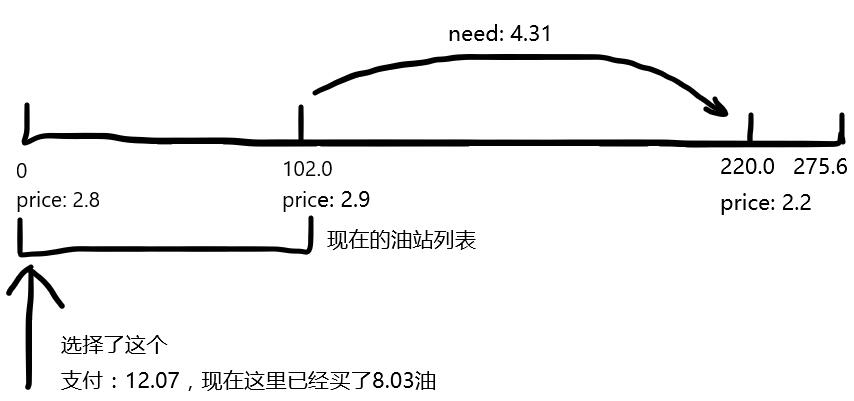
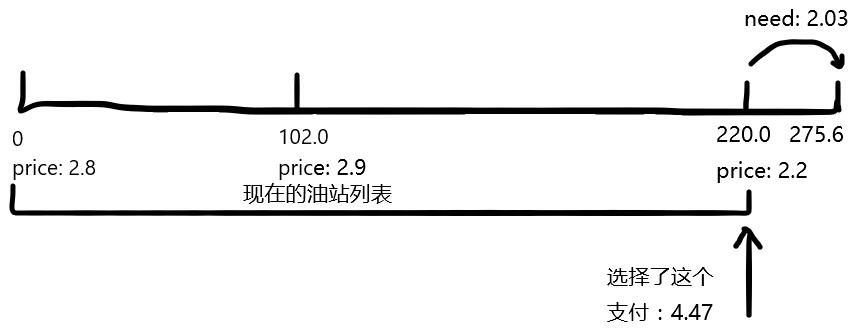
实现上,列表用堆/优先队列维护,可以将起点、终点作为油站加入列表,走到终点结束前进即可。实现代码中有详细注释。
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
struct gas {
double pos, price, vol;
} g[505];
bool cmp(gas a, gas b) {
return a.pos < b.pos;
}
struct cmp1 {
bool operator()(int a, int b) {
return g[a].price > g[b].price;
}
};
priority_queue<int, vector<int>, cmp1> pq; // 堆存可以用的油
int n; // 注意n可以为0
double dis, vol, doil, sprice, maxdis;
int main() {
scanf("%lf%lf%lf%lf%d", &dis, &vol, &doil, &sprice, &n);
maxdis = vol * doil;
if(n == 0) { // 对n为0的特判
if(dis > maxdis) {
printf("No Solution");
} else {
printf("%.2lf", dis / doil * sprice);
}
return 0;
}
// 把起点和终点都加入加油站的列表
g[0].pos = 0, g[0].price = sprice, g[0].vol = 0;
g[n + 1].pos = dis, g[n + 1].price = -1, g[n + 1].vol = -1;
for(int i = 1; i <= n; i++) {
scanf("%lf%lf", &g[i].pos, &g[i].price);
g[i].vol = 0;
}
sort(g, g + n + 1, cmp);
pq.push(0);
int ngas = 0; // 表示现在开到了下表为ngas的加油站
double ncost = 0; // 表示现在的累计花费油钱
while(ngas < n + 1) {
//printf("maxdis %lf dis %lf\n", maxdis, g[ngas].pos - g[pq.top()].pos);
// 如果走的太远远处的油站就无法加油了,或是这个油站已经买了一箱油没办法再加了,这两种情况要把油站出堆
while(g[ngas].pos - g[pq.top()].pos > maxdis || g[pq.top()].vol >= vol) {
pq.pop();
}
// 无解的情况:存在相邻油站距离大于一箱油可以支持的距离
if(g[ngas + 1].pos - g[ngas].pos > maxdis) {
printf("No Solution");
return 0;
}
int gmin = pq.top();
pq.pop();
//printf("ngas %d ncost %lf gmin pos %lf price %lf vol %lf\n", ngas, ncost, g[gmin].pos, g[gmin].price, g[gmin].vol);
double gcost = (g[ngas + 1].pos - g[ngas].pos) / doil;
// 往前走一个油站,计算这段路程的油费开支
if(vol - g[gmin].vol >= gcost) { // 如果最便宜的油能够支持这一段路程
ncost += gcost * g[gmin].price;
g[gmin].vol += gcost;
} else { // 如果最便宜的油不能支持这一段路程,那么就要补充次便宜的
while(gcost > 1e-10) { // EPS设为1e-10避免浮点陷阱
double navailable = vol - g[gmin].vol; // 现在选择的油站可以买的油量
ncost += min(gcost, navailable) * g[gmin].price;
gcost = max(1e-10, gcost - navailable);
g[gmin].vol = min(vol, g[gmin].vol + gcost);
while(g[ngas].pos - g[pq.top()].pos > maxdis || g[pq.top()].vol >= vol) {
pq.pop();
}
gmin = pq.top();
}
}
ngas++;
pq.push(gmin); // 把还能加的油加进去
pq.push(ngas);
}
printf("%.2lf", ncost);
return 0;
}