[CF2B]The least round way 题解
题目地址:Codeforces:Problem – 2B – Co …
May all the beauty be blessed.
游戏地址:拠点 | エンジニアが死滅シタ世界 〜アンドロイドとふたりぼっちで生きろ〜(需要paiza账号)
近日玩了下paiza社《エンジニアが死滅シタ世界 〜アンドロイドとふたりぼっちで生きろ〜》游戏(译名:《工程师死绝的世界》),将其中的问题翻译了一下(原谅我低下的语文水平)并且试着写了解答,在这里跟各位分享一下。希望通过各种渠道点进来的各位多多关注本博客呀~
难度BCD的问题都是些比较基础的实现题,难度A的问题目测是一个乱搞题,类似于OI中的提交答案题一样,不过没有兴趣研究就没留题解。
离线版资源合集下载:botchi_translations.zip
点击表中对应连接进入题目:
(注:按ABCD的顺序难度递减)
难度A:
难度B:
难度C:
难度D:
Translation by KSkun
原题:問題「荒れ果てたショップ」 | エンジニアが死滅シタ世界 〜アンドロイドとふたりぼっちで生きろ〜
你正在整理商店管理系统的文件。
每个文件有编号与之对应,为了让文件的编号看起来比较一致,比较短的数字需要在左边补0至长度相同。
例如,编号的长度为3时,0应该补成000,而4应该补成004,13补成013,144不需要补0因此就是144,诸如此类。
给你三个整数N、A和B。
你需要将区间[A, B]中的整数补0至长度都为N,然后输出他们。
例如,样例1可以表示为下图。
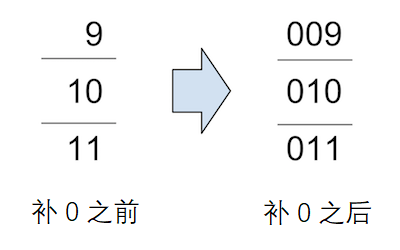
在这个样例中,你需要将9、10和11三个数字补成长度为3的统一形式。
N A B
将区间[A, B]中的每一个整数i补成长度为N的形式并分别输出他们。
输出的最后应该包含一个换行符。
输入:
3 9 11
输出:
009
010
011
输入:
2 0 3
输出:
00
01
02
03
// Code by KSkun, 2019/1
#include <cstdio>
#include <cctype>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
LL res = 0, neg = 1; char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
char c;
while(!isgraph(c = fgc())) {}
return c;
}
int n, a, b;
char fmt[10];
int main() {
n = readint(); a = readint(); b = readint();
sprintf(fmt, "%%0%dd\n", n);
for(int i = a; i <= b; i++) {
printf(fmt, i);
}
return 0;
}
Translation by KSkun
原题:問題「高層タワー」 | エンジニアが死滅シタ世界 〜アンドロイドとふたりぼっちで生きろ〜
你在把一些单词组合成新的单词。
新单词由N个字符串按先后顺序结合而成。
为了避免新单词过于冗长,需要将前一个单词的末端与后一个单词的前端最长的相同子串合并起来。
例如,样例1中需要合并paiza、apple和letter三个单词,
前两个单词paiza和apple按要求合并后得到了paizapple这个单词。
再合并上后一个单词就得到了paizappletter。
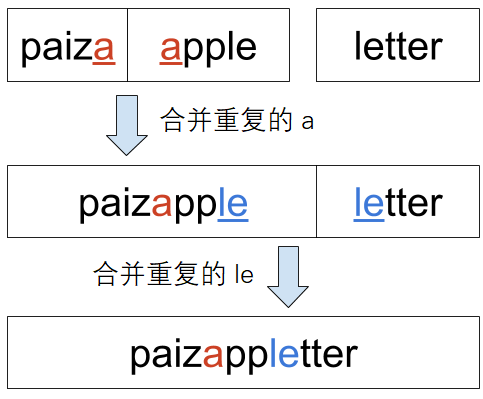
注意,必须按从前到后的顺序合并,样例2中合并poh、p、oh时,
poh和p合并得到了pohp,此时再合并oh得到的是pohpoh。
请按照输入的先后顺序合并给出的N个字符串得到新单词。
N
w_1
w_2
...
w_N
输出N个单词按输入先后顺序结合成的新单词。
输入:
3
paiza
apple
letter
输出:
paizappletter
输入:
3
poh
p
oh
输出:
pohpoh
// Code by KSkun, 2019/1
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
LL res = 0, neg = 1; char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
char c;
while(!isgraph(c = fgc())) {}
return c;
}
const int MAXN = 10005;
int n, rlen = 0, len;
char res[MAXN], w[MAXN];
inline bool issame(int len) {
for(int i = 1; i <= len; i++) {
if(res[rlen - (len - i)] != w[i]) return false;
}
return true;
}
inline int solve(int len) {
for(int i = std::min(rlen, len); i >= 1; i--) {
if(issame(i)) return i;
}
return 0;
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%s", w + 1);
len = strlen(w + 1);
int r = solve(len);
for(int i = 1; i <= len - r; i++) {
res[rlen + i] = w[r + i];
}
rlen += len - r;
}
printf("%s", res + 1);
return 0;
}