2019年11月5日

[IOI2007]Pairs 题解

[IOI2007]Pairs 题解

题目地址：洛谷：P4648 [IOI2007] pairs 动物对数 – 洛谷 | 计算机科学教育新生态、BZOJ：Problem 1807. — [Ioi2007]Pairs 彼此能听得见的动物对数

题目描述

Mirko and Slavko are playing with toy animals. First, they choose one of three boards given in the figure below. Each board consists of cells (shown as circles in the figure) arranged into a one, two or three dimensional grid.

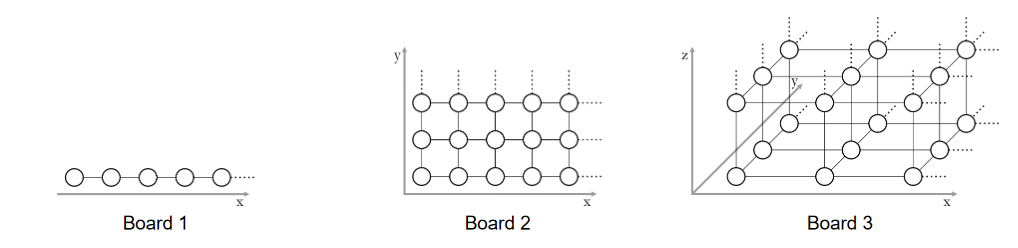
Mirko then places N little toy animals into the cells.

The distance between two cells is the smallest number of moves that an animal would need in order to reach one cell from the other. In one move, the animal may step into one of the adjacent cells (connected by line segments in the figure).

Two animals can hear each other if the distance between their cells is at most D. Slavko’s task is to calculate how many pairs of animals there are such that one animal can hear the other.

Write a program that, given the board type, the locations of all animals, and the number D, finds the desired number of pairs.

题意简述

在一维、二维、三维空间中有 $N$ 个点，请你求出其中曼哈顿距离不超过 $D$ 的点对数。

输入输出格式

输入格式：

The first line of input contains four integers in this order:

  • The board type B (1 ≤ B ≤ 3);
  • The number of animals N (1 ≤ N ≤ 100000);
  • The largest distance D at which two animals can hear each other (1 ≤ D ≤ 100000000);
  • The size of the board M (the largest coordinate allowed to appear in the input):
    • When B=1, M will be at most 75000000.
    • When B=2, M will be at most 75000.
    • When B=3, M will be at most 75.

Each of the following N lines contains B integers separated by single spaces, the coordinates of one toy animal.

Each coordinate will be between 1 and M (inclusive).

More than one animal may occupy the same cell.

输出格式：

Output should consist of a single integer, the number of pairs of animals that can hear each other. Note: use a 64-bit integer type to calculate and output the result (long long in C/C++, int64 in Pascal).

输入输出样例

输入样例#1：

1 6 5 100 
25 
50 
50 
10 
20 
23

输出样例#1：

4

输入样例#2：

2 5 4 10 
5 2 
7 2 
8 4 
6 5 
4 4

输出样例#2：

8

输入样例#3：

3 8 10 20 
10 10 10 
10 10 20 
10 20 10 
10 20 20 
20 10 10 
20 10 20 
20 20 10 
20 20 20

输出样例#3：

12

题解

这是 IOI 问题中的一道“胶水题”。实际上 B=1 、 B=2 、 B=3 三种情况使用的算法都并不相同，但又能通过低维最优解扩展（实际上是对多出来的一维做暴力）得到一个不那么优的做法骗到分，个人觉得这也是一种挺不错的命题方式。

B=1 ：双指针

很容易发现，将一维点按照坐标从小到大排序得到序列 $\{a_i\}$ ，对于元素 $a_i$ ，记到这个点距离不超过 $D$ 的坐标最小的点为 $a_j$ ，则下标在 $[j, i]$ 范围内的点都是当元素 $a_i$ 作为右边的那个点（只统计 $a_i$ 作为右边的情况是为了去重）时构成的点对的左边的那个点的选择， $a_i$ 对答案的贡献值为 $(i-j)$ 。此处的 $j$ 随 $i$ 的增大而增大，因此可以应用双指针算法。

指针 $i$ 和 $j$ 各自的移动次数都不超过 $N$ ，因此复杂度为 $O(N)$ 。

B=2 ：转换坐标系与扫描线（树状数组）

如果将扫描线应用到 $x$ 坐标为定值的每一“行”中，也是能解决二维问题的，因为每一行 $y$ 坐标的区间长度不会改变。但这样做复杂度会高达 $O(N^2D)$ ，与 $D$ 有关，不是一个可取的方法。

为了让问题更好处理，这里使用了转换坐标系的技巧。容易发现的性质是，一个二维点所有距离在 $D$ 之内的点构成了一个倾斜 $45^{\circ}$ 的正方形，如果把坐标系旋转 $45^{\circ}$ 就可以转成一个边与坐标轴平行的正方形，就好处理了一些。然而因为旋转坐标系需要涉及 $\frac{\sqrt{2}}{2}$ 的计算，并不是那么好写。

一个更好实现的方法是引入切比雪夫距离。

定义 1 两个 $n$ 维空间点的切比雪夫距离定义为所有维度坐标值之差的绝对值的最大值，即两个二维点 $(x_1, y_1), (x_2, y_2)$ 的切比雪夫距离为 $\text{dist} = \max\{ |x_1-x_2|, |y_1-y_2| \}$ 。

引理 1 两个二维点 $(x_1, y_1), (x_2, y_2)$ 的曼哈顿距离等于 $(x_1+y_1, x_1-y_1), (x_2+y_2, x_2-y_2)$ 两个点的切比雪夫距离。

引理 1 的证明可以将两种距离分情况展开成表达式，容易观察到两个距离的表达式完全等价。

对二维空间的所有点做坐标转换（以下所有坐标都为转换后的坐标），则曼哈顿距离上的限制就变成了切比雪夫距离上的限制，此时与点 $P$ 距离不超过 $D$ 的点就变成了一个长为 $2D$ ，以 $P$ 为几何中心的一个正方形，这将问题转化为在这个正方形中求点数的问题，可以用扫描线来解决。

用一个树状数组（也可使用线段树或其他功能相同的数据结构）存储在规定的 $x$ 坐标范围内，每个 $y$ 坐标上的点数。点 $(x_i, y_i)$ 的贡献即为树状数组中 $[y_i-D, y_i+D]$ 范围内的点数，计算前要先将树状数组中 $x_j < x_i-D$ 的点 $(x_j, y_j)$ 移除，计算后要将当前计算的点 $(x_i, y_i)$ 插入树状数组。

树状数组的插入、删除、查询操作不会超过 $3N$ 次，而树状数组的大小为坐标数值上限 $M$ ，因此该算法的复杂度为 $O(N \log M)$ 。

由于坐标转换时 $(x_i-y_i)$ 可能为负值，不妨在树状数组中将其存储为 $(x_i-y_i+M)$ ，计算时再复原回去即可，细节见代码。

B=3 ：二维前缀和

你依然可以将 B=2 的扫描线做法扩展到三维，原理是对 $z$ 坐标暴力，固定 $z$ 坐标可以得到一个平面，在该平面用该平面的修正距离 限制 （对于三维点 $(x, y, z)$ ，它在 $z$ 坐标为 $z’$ 的平面内的距离限制为 $(D-|z-z’|)$ ）做扫描线即可。但此时的复杂度依然与 $D$ 有关，不是可取的方法。

观察到 $M$ 的范围很小，实际上 $z$ 坐标只需要检查至多 $M$ 次，也就是说当 $M$ 大于 $3M$ 时就无意义了， $D$ 的值可以变得很小。

而且坐标值的范围变小为我们应用二维前缀和提供了便利，分别对每个固定 $z$ 坐标得到的平面上的点做一次前缀和，利用前缀和的值可以单次 $O(1)$ 地查到一个正方形中的点数。这可以替代扫描线中对树状数组的查询操作，且前缀和都进行了预处理，不需要维护树状数组了。

但这导致了一个问题，在查询点所在的 $z$ 坐标固定形成的平面中查询的答案存在重复，因此要单独做一次去重，细节见代码。

求前缀和的复杂度为 $O(M^3)$ ，计算的复杂度为 $O(NM)$ ，因此最终复杂度为 $O(NM)$ 。

代码

// Code by KSkun, 2019/10
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>
#include <vector>

typedef long long LL;

inline char fgc() {
	static char buf[100000], * p1 = buf, * p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
		? EOF : *p1++;
}

inline LL readint() {
	LL res = 0, neg = 1; char c = fgc();
	for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
	for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
	return res * neg;
}

inline char readsingle() {
	char c;
	while(!isgraph(c = fgc())) {}
	return c;
}

const int MAXN = 100005;

int B, n, D, m;
int sum[80][505][505];

class BinaryIndexedTree {
private:
	inline static int lowbit(int x) {
		return x & -x;
	}
	int N;
	std::vector<int> dat;
public:
	BinaryIndexedTree(int _N = 240) {
		N = _N;
		dat.assign(N, 0);
	}
	void add(int pos, int value) {
		for (int i = pos; i < N; i += lowbit(i)) {
			dat[i] += value;
		}
	}
	int query(int pos) {
		if (pos <= 0) return 0;
		int res = 0;
		for (int i = pos; i > 0; i -= lowbit(i)) {
			res += dat[i];
		}
		return res;
	}
	void clear() {
		dat.clear();
		dat.assign(N, 0);
	}
};

struct Pos {
	int x, y, z;
	Pos(int _x = 0, int _y = 0, int _z = 0): x(_x), y(_y), z(_z) {}
	inline bool operator<(const Pos& rhs) const {
		return z != rhs.z ? z < rhs.z : (x != rhs.x ? x < rhs.x : y < rhs.y);
	}
} pos[MAXN];

int main() {
	B = readint(); n = readint(); D = readint(); m = readint();
	for (int i = 1, x, y; i <= n; i++) {
		x = readint();
		if (B >= 2) y = readint();
		if (B >= 3) pos[i].z = readint();
		
		// 坐标转换
		if (B >= 2) {
			pos[i].x = x + y;
			pos[i].y = x - y + m; // 避免产生负值
		} else {
			pos[i].x = x;
		}
	}
	std::sort(pos + 1, pos + n + 1);

	LL ans = 0;
	if (B == 1) { // 双指针
		int lft = 1;
		for (int i = 1; i <= n; i++) {
			lft = std::lower_bound(pos + lft, pos + i, Pos(pos[i].x - D)) - pos;
			ans += i - lft;
		}
	} else if (B == 2) { // 扫描线
		BinaryIndexedTree bit(225005); int lst = 1;
		bit.add(pos[1].y, 1);
		for (int i = 2; i <= n; i++) {
			while (lst < i && pos[i].x - pos[lst].x > D) {
				bit.add(pos[lst].y, -1);
				lst++;
			}
			int l = std::max(0, pos[i].y - D), r = std::min(m * 2, pos[i].y + D);
			int res = bit.query(r) - bit.query(l - 1);
			ans += res;
			bit.add(pos[i].y, 1);
		}
	} else { // 二维前缀和
		D = std::min(D, m * 3); // 缩小 D 的范围
		for (int i = 1; i <= n; i++) {
			sum[pos[i].z][pos[i].x][pos[i].y]++;
		}
		for (int i = 1; i <= m; i++) {
			for (int j = 1; j < 505; j++) {
				for (int k = 1; k < 505; k++) {
					sum[i][j][k] += sum[i][j - 1][k] + sum[i][j][k - 1] - sum[i][j - 1][k - 1];
				}
			}
		}
		LL ans2 = 0;
		for (int i = 1; i <= n; i++) {
			for (int j = std::max(1, pos[i].z - D); j < pos[i].z; j++) {
				int d = D - (pos[i].z - j); auto arr = sum[j];
				int x1 = std::max(1, pos[i].x - d), y1 = std::max(1, pos[i].y - d), x2 = pos[i].x + d, y2 = pos[i].y + d;
				ans += arr[x2][y2] - arr[x1 - 1][y2] - arr[x2][y1 - 1] + arr[x1 - 1][y1 - 1];
			}
			auto arr = sum[pos[i].z];
			int x1 = std::max(1, pos[i].x - D), y1 = std::max(1, pos[i].y - D), x2 = pos[i].x + D, y2 = pos[i].y + D;
			ans2 += arr[x2][y2] - arr[x1 - 1][y2] - arr[x2][y1 - 1] + arr[x1 - 1][y1 - 1];
		}
		ans2 -= n; // 去重
		ans += ans2 / 2;
	}

	printf("%lld", ans);
	return 0;
}
Author:
Filed Under: 题解, 算法, IOI
Tags: , , ,

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

此站点使用Akismet来减少垃圾评论。了解我们如何处理您的评论数据。