2018年6月30日
回文自动机原理与实现

概述
回文自动机(简称PAM,又称回文树,Palindromic Tree)是一种用于处理回文串的结构,在其结构内可以找到原串中的所有回文子串,经由APIO2014推广。下面对其原理及实现进行介绍。
本文中所有图片来自网络,感谢其作者的贡献。
结构
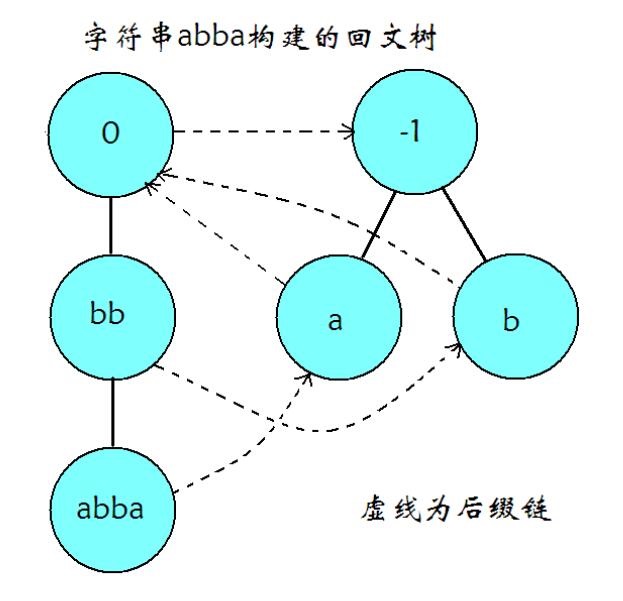
如图为串abba的PAM示意图,其中,实现表示回文串的扩展转移边,虚线表示后缀链接。
回文树
回文树是PAM的一部分,一个PAM包含两棵回文树,分别代表奇偶回文串。每棵回文树上,所有节点(除树根以外)都代表了一个回文子串。每条转移边上都有一个字符,若某点对应的回文子串为$S$,它的一条出边上字符为$c$,则会转移至一个代表$c+S+c$串的节点。从树根出发的每条路径,都对应着一个回文子串,如果将路径上边的字符顺次连接,将会得到回文串的右半部分。
节点信息
- 每个节点上记录对应回文串的长度$\mathrm{len}(u)$,若节点$v$是节点$u$转移而来的,则有$\mathrm{len}(v) = \mathrm{len}(v) + 2$。为了方便,我们规定,偶回文树树根$\mathrm{len}(rt_0)=0$,奇回文树树根$\mathrm{len}(rt_1)=-1$。
如abba的PAM中,节点$u$代表串bb,节点$v$代表串abba,存在$u \rightarrow v$的转移边,$\mathrm{len}(u)=2$且$\mathrm{len}(v)=4$。 - 每个节点记录该节点对应回文串的出现次数$\mathrm{siz}(u)$。在回文树中,除了根节点以外,所有节点满足$\mathrm{siz}(u)>0$。
转移边
转移边$u \rightarrow v$对节点的意义是,将$u$对应的回文串左右两边加上同一个字符$c$得到节点$v$对应的回文串。由于$u$对应的回文串是$v$对应的回文串的子串,因此,$v$对应的回文串出现的地方,$u$对应的回文串也出现了。
后缀链接
- $u$的后缀链接指向$v$,记作$\mathrm{fail}(u)=v$,当且仅当$v$对应的回文串是$u$对应的回文串的一个后缀,且不存在其他的$v’$,使得$\mathrm{len}(v’) > \mathrm{len}(v)$且满足上一句话的性质。这里的后缀链接的意义与AC自动机、KMP匹配算法的fail数组意义很像。
例如,对于abba的PAM,对应abba的节点$u$与对应a的节点$v$,存在$\mathrm{fail}(u)=v$。 - 为了方便,我们规定,偶回文树树根的后缀链接指向奇回文树树根,即$\mathrm{fail}(rt_0)=rt_1$。
- 后缀链接构成了一棵以奇回文树树根为根的有根树,方向从叶子指向根。
构造
流程
PAM的构造法在字符集为常数且较小时,是线性复杂度的。与SAM相似的是,PAM的构造法也是一个增量算法,因此,应该解释为,每次在母串后插入一个字符,更新PAM的复杂度是$O(1)$的。
PAM中,我们需要记下上一次插入的节点位置,即$lst$。
下面,我们结合例子解释插入的过程。
如图,为串abba的PAM,我们向其插入新字符a。
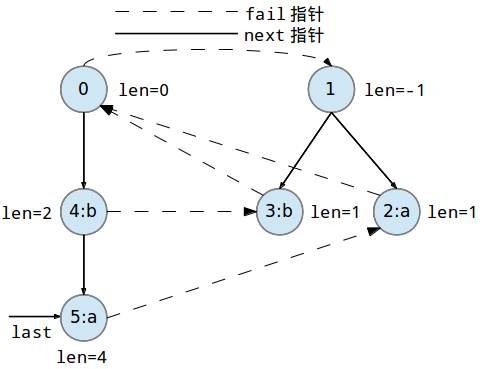
- 从上一次插入的节点位置$lst$开始沿$\mathrm{fail}(u)$上跳,找到第一个节点,使得该节点对应的一个母串的后缀后加上插入的字符$c$构造出了一个新的回文后缀。
在本例中,abba后加入字符a构成的新串是abbaa,这一过程实际上是找到一个新串的一个最长回文后缀,也就是aa的父节点,我们找到的是偶回文树的树根$0$。 - 若查询到该回文串已存在节点,则对该节点$\mathrm{siz}(u)$加1。
- 若不存在该回文串的节点,则在父节点下新建节点,并采用与1相似的过程,从父节点沿$\mathrm{fail}(u)$上跳,直到找到一个第一个最长的回文后缀,从而计算出该节点的$\mathrm{fail}(u)$值。
在本例中,aa回文串的最长回文后缀是a,容易发现,从父节点$0$开始上跳,会跳到奇回文树根$1$,从而找到对应的最长回文后缀节点$2$,即对于新加点$u=6$,有$\mathrm{fail}(6)=2$。 - 更新PAM的$lst$值及刚才插入的回文后缀的$\mathrm{siz}(u)$值。
经过上面一通处理,现在,PAM的结构变为了下图的样子。
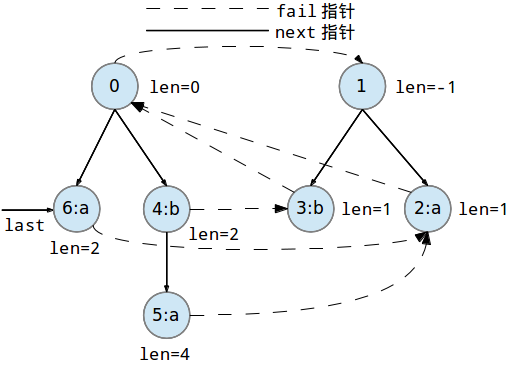
实现
参见例题。
例题:[APIO2014]回文串
点击标题进入文章。
常见应用
本质不同回文子串数目
即后缀树中节点的数量。
每个回文子串出现的次数
先按逆序(拓扑序)更新父节点$\mathrm{siz}(u)$值然后就可以直接拿来用了。

sto