题目地址：洛谷：【P4724】[ZJOI2007]粒子运动 – 洛谷、BZOJ：Problem 1094. — [ZJOI2007]粒子运动

题目描述

阿Q博士正在观察一个圆形器皿中的粒子运动。不妨建立一个平面直角坐标系，圆形器皿的圆心坐标为(x0, y0
)，半径为R。器皿中有若干个粒子，假设第i个粒子在时刻0的位置为(xi, yi)，速度为(vxi,vyi)（注：这是一个速度向量，若没有发生碰撞，t时刻的位置应该是(xi + t * vxi, yi + t * vyi) ）。假设所有粒子的运动互不干扰；若某个粒子在某个时刻碰到了器皿壁，将发生完全弹性碰撞，即速度方向按照碰撞点的切线镜面反射，且速度大小不变（如图）。认为碰撞是瞬间完成的。

尽管碰撞不会影响粒子的速率，但是粒子却会受到一定的伤害，所以若某一个粒子碰撞了k次器皿壁，那么在第k次碰撞时它便会消亡。
出于研究的需要，阿Q博士希望知道从时刻0到所有粒子都消亡这段时间内，所有粒子之间的最近距离是什么。你能帮助他么？

题意简述

圆形容器中有$n$个粒子，各给定初始位置和速度，粒子会与容器壁碰撞，碰撞时发生反射，如图，速度会改变方向但不改变大小。每个粒子最多能和容器壁碰撞$k$次，否则会消失。求所有时刻所有粒子两两距离的最小值。

输入输出格式

输入格式：
第一行包含三个实数，分别为x0, y0, R，即圆形器皿的圆心坐标及半径。第二行包含两个正整数N, k，分别表示粒子的总数与消亡碰撞次数。接下来N行每行四个实数，分别为xi, yi, vxi , vyi，保证(xi, yi)都在圆内且(vxi, vyi)非零。

输出格式：
仅包含一个实数，即所有粒子的历史最近距离，精确到小数点后三位。

输入输出样例

输入样例#1：

0 0 10
2 10
0 -5 0 1
5 0 1 0

输出样例#1：

7.071

说明

对于所有的数据，2 ≤N ≤100。1≤k ≤100。
请注意实数精度问题。

题解

没用到计算几何算法的计算几何题。
我们考虑，在一段连续时间内，研究两个粒子的距离，假如在这段时间内不发生碰撞，则距离可以表示为一个二次函数，假设第一个粒子的位置可以表示为$P+tV$（$P$是起始位置，$V$是速度向量），第二个可以表示为$P’+tV’$，则可以列出距离的表达式$f(t) = \mathrm{length}[(P+tV) – (P’+tV’)]$，展开后得到一个二次函数。既然是二次函数，我们可以在$O(1)$时间内求得区间最小值。
因此，本题的大体思路是，枚举每两个粒子，在每一个两个粒子都不发生碰撞的连续区间内求区间最小距离，来更新最后的答案。这个复杂度是$O(n^2k)$的。
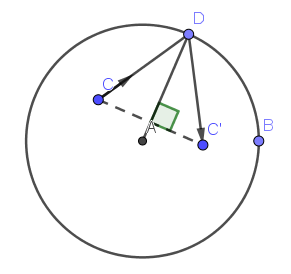
我用了对称的方法解决反射的速度变化，先把射线的起点对称至碰撞点处的半径另一侧，然后在另一侧构造新的速度向量，并处理长度即可。过程如图所示。

代码

// Code by KSkun, 2018/7
#include <cstdio>
#include <cctype>
#include <cmath>

#include <algorithm>

const int MAXN = 105;
const double EPS = 1e-8, PI = acos(-1);

inline int dcmp(double x) {
    if(fabs(x) < EPS) return 0; else return x < 0 ? -1 : 1;
}

struct Vector {
    double x, y;
    Vector(double x = 0, double y = 0) : x(x), y(y) {}
    inline Vector operator+(Vector rhs) {
        return Vector(x + rhs.x, y + rhs.y);
    }
    inline Vector operator-(Vector rhs) {
        return Vector(x - rhs.x, y - rhs.y);
    }
    inline Vector operator*(double rhs) {
        return Vector(x * rhs, y * rhs);
    }
    inline Vector operator/(double rhs) {
        return Vector(x / rhs, y / rhs);
    }
};

typedef Vector Point;

inline double dot(Vector u, Vector v) {
    return u.x * v.x + u.y * v.y;
}

inline double cross(Vector u, Vector v) {
    return u.x * v.y - u.y * v.x;
}

inline double length(Vector v) {
    return sqrt(dot(v, v));
}

inline double angle(Vector u, Vector v) {
    return acos(dot(u, v) / length(u) / length(v));
}

inline Vector rotate(Vector v, double rad) {
    return Vector(v.x * cos(rad) - v.y * sin(rad), v.x * sin(rad) + v.y * cos(rad));
}

struct Line {
    Point p; Vector v;
    Line(Point p = Point(), Vector v = Vector()) : p(p), v(v) {}
};

struct Ray : public Line {
    Ray(Point p = Point(), Vector v = Vector()) : Line(p, v) {}
};

struct Circle {
    Point c; double r;
    Circle(Point c = Point(), double r = 0) : c(c), r(r) {}
};

inline Point intersection(Circle o, Ray l) {
    double x0 = o.c.x, y0 = o.c.y, a = l.p.x, b = l.p.y, c = l.v.x, d = l.v.y;
    double A = c * c + d * d, B = 2 * (a * c - c * x0 + b * d - d * y0), 
        C = a * a - 2 * a * x0 + x0 * x0 + b * b - 2 * b * y0 + y0 * y0 - o.r * o.r;
    double delta = B * B - 4 * A * C;
    double t1 = (-B + sqrt(delta)) / 2 / A, t2 = (-B - sqrt(delta)) / 2 / A;
    if(dcmp(t1) > 0) return l.p + l.v * t1; else return l.p + l.v * t2;
}

inline Point projection(Line l, Point p) {
    return l.p + l.v * (dot(l.v, p - l.p) / dot(l.v, l.v));
}

inline double distance(Point p1, Point p2) {
    return length(p1 - p2);
}

inline double getmin(double A, double B, double C, double l, double r) {
    double v1 = A * l * l + B * l + C, v2 = A * r * r + B * r + C, v3 = 1e10;
    double m = -B / 2 / A;
    if(m >= l && m <= r) v3 = A * m * m + B * m + C;
    return std::min(std::min(v1, v2), v3);
}

Circle o;
int n, k;
Point p[MAXN];
Vector v[MAXN];

inline double sqr(double x) {
    return x * x;
}

inline double getmin(int a, int b) {
    int ak = 0, bk = 0; double res = 1e10;
    Ray ra(p[a], v[a]), rb(p[b], v[b]);
    while(ak < k && bk < k) {
        Point ai = intersection(o, ra), bi = intersection(o, rb);
        double t1 = distance(ra.p, ai) / length(ra.v), t2 = distance(rb.p, bi) / length(rb.v);
        double nt = std::min(t1, t2);
        double A = sqr(ra.v.y - rb.v.y) + sqr(ra.v.x - rb.v.x),
            B = 2 * ((ra.p.y - rb.p.y) * (ra.v.y - rb.v.y) 
                + (ra.p.x - rb.p.x) * (ra.v.x - rb.v.x)),
            C = sqr(ra.p.y - rb.p.y) + sqr(ra.p.x - rb.p.x);
        res = std::min(res, getmin(A, B, C, 0, nt));
        if(dcmp(nt - t1) == 0) {
            ak++; 
            Point proj = projection(Line(o.c, o.c - ai), ra.p);
            Point p1(proj.x * 2 - ra.p.x, proj.y * 2 - ra.p.y);
            Vector v1 = p1 - ai; v1 = v1 / length(v1) * length(ra.v);
            ra.p = ai; ra.v = v1;
        } else {
            ra.p = ra.p + ra.v * nt;
        }
        if(dcmp(nt - t2) == 0) {
            bk++; 
            Point proj = projection(Line(o.c, o.c - bi), rb.p);
            Point p1(proj.x * 2 - rb.p.x, proj.y * 2 - rb.p.y);
            Vector v1 = p1 - bi; v1 = v1 / length(v1) * length(rb.v);
            rb.p = bi; rb.v = v1;
        } else {
            rb.p = rb.p + rb.v * nt;
        }
    }
    return res;
}

int main() {
    double x0, y0, r;
    scanf("%lf%lf%lf", &x0, &y0, &r);
    o = Circle(Point(x0, y0), r);
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) {
        double xi, yi, vxi, vyi;
        scanf("%lf%lf%lf%lf", &xi, &yi, &vxi, &vyi);
        p[i] = Point(xi, yi); v[i] = Vector(vxi, vyi);
    }
    double ans = 1e10;
    for(int i = 1; i <= n; i++) {
        for(int j = i + 1; j <= n; j++) {
            ans = std::min(ans, getmin(i, j));
        }
    }
    printf("%.3lf", dcmp(ans) > 0 ? sqrt(ans) : 0);
    return 0;
}