概述

可持久化线段树是一类线段树的实现方式，用于保存线段树的历史版本。本文后半部分所介绍的一种用法是主席树这一类可持久化线段树。主席树是以下标为时间加入元素的一类可持久化线段树，常见的用法是静态查询区间第k大值。下面我们介绍它的原理和实现。

原理

什么叫“可持久”？

可持久的意思是保存历史版本，可以查询到历史操作的结果。比如，对于一个序列进行更改，你可以选择每一次更改前将上次更改后的序列复制一份，再在新序列中更改，以保留这个序列的所有历史版本。同样地，你也可以建一堆线段树来保留线段树的历史版本。但是，这样做的空间是O(Q * 4N)的，显然很难接受，因此我们要使用可持久化线段树这种实现方法。

结构

一棵可持久化线段树的结构如图所示。

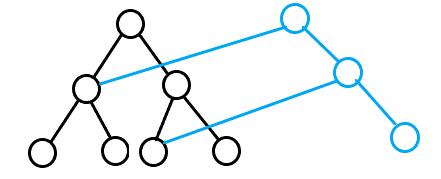
如图，黑色的为最初版本的线段树，蓝色的为版本2。

修改

如示例图所示，线段树的修改应该是修改一条链，也就是两个相邻版本的的线段树只会有一条链有差别。那我们考虑动态开点，将后面版本的线段树那些没有更改的儿子指向前一个版本的线段树的节点，这样每次只会新建一条链的节点，空间降低为O(4N + Q \log N)，是可以接受的了。

查询

每次修改后存储这一次修改的新线段树的根，然后按照根下去正常查询即可。

实现

修改

每次修改前令本次的根为上一次的根，再执行下面的操作。

inline void insert(int &o, int l, int r, int x) {
    tree[++tot] = tree[o];
    o = tot;
    tree[o].val++;
    if(l == r) return;
    int mid = (l + r) >> 1;
    if(x <= mid) insert(tree[o].lch, l, mid, x);
    else insert(tree[o].rch, mid + 1, r, x);
}

查询

常规操作，不提供实现细节。

主席树（查询区间k小值）

原理

我们考虑使用权值线段树，对原序列一个一个插入可持久化线段树。这样，线段树对应区间就是前若干数中该区间内数的个数。对于查询，我们考虑第r和第l-1棵线段树，对应区间值的差就是询问区间中的答案。所以我们的查询操作可以同时沿着这两棵线段树走。

实现

以下是查询操作的实现。

inline int query(int o1, int o2, int l, int r, int k) {
    if(l == r) return l;
    int mid = (l + r) >> 1;
    int num = tree[tree[o2].lch].val - tree[tree[o1].lch].val;
    if(k <= num) return query(tree[o1].lch, tree[o2].lch, l, mid, k);
    else return query(tree[o1].rch, tree[o2].rch, mid + 1, r, k - num);
}

代码

本代码可以通过【P3834】【模板】可持久化线段树 1（主席树） – 洛谷一题。

// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int readint() {
    register int res = 0, neg = 1;
    char c = fgc(); 
    while (c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while (c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MAXN = 200005;

struct Node {
    int lch, rch, val;
} tree[MAXN << 5];
int tot = 0, rt[MAXN];

inline void insert(int &o, int l, int r, int x) {
    tree[++tot] = tree[o];
    o = tot;
    tree[o].val++;
    if(l == r) return;
    int mid = (l + r) >> 1;
    if(x <= mid) insert(tree[o].lch, l, mid, x);
    else insert(tree[o].rch, mid + 1, r, x);
}

inline int query(int o1, int o2, int l, int r, int k) {
    if(l == r) return l;
    int mid = (l + r) >> 1;
    int num = tree[tree[o2].lch].val - tree[tree[o1].lch].val;
    if(k <= num) return query(tree[o1].lch, tree[o2].lch, l, mid, k);
    else return query(tree[o1].rch, tree[o2].rch, mid + 1, r, k - num);
}

int n, m, a[MAXN], tmp[MAXN],ttot, l, r, k;

int main() {
    n = readint();
    m = readint();
    for(int i = 1; i <= n; i++) {
        a[i] = tmp[i] = readint();
    }
    std::sort(tmp + 1, tmp + n + 1);
    ttot = std::unique(tmp + 1, tmp + n + 1) - tmp - 1;
    for(int i = 1; i <= n; i++) {
        rt[i] = rt[i - 1];
        insert(rt[i], 1, ttot, std::lower_bound(tmp + 1, tmp + ttot + 1, a[i]) - tmp);
    } 
    while(m--) {
        l = readint();
        r = readint();
        k = readint();
        printf("%d\n", tmp[query(rt[l - 1], rt[r], 1, ttot, k)]);
    }
    return 0;
}