2018年3月1日

Splay原理与实现

Splay原理与实现

注：本文部分图片来自互联网，其相关权利归原作者所有，感谢原作者的分享。

概述

Splay（伸展树）是异于Treap的另一种平衡树，由Tarjan等发明。其滋磁的操作更为通用，因此被OIer广为使用。这里介绍Splay的原理与实现。

原理与实现

旋转

旋转操作与Treap相同，可以在Treap原理与实现 | KSkun’s Blog查看示例。这里将左右旋换为了一种自适应的写法。
下面是旋转的实现。

inline void rotate(int p) { // p is child
    bool type = !isleft(p);
    int fa = tr[p].fa, ffa = tr[fa].fa;
    tr[fa].ch[type] = tr[p].ch[!type];
    tr[p].ch[!type] = fa;
    tr[tr[fa].ch[type]].fa = fa;
    if(ffa) tr[ffa].ch[!isleft(fa)] = p;
    tr[p].fa = tr[fa].fa;
    tr[fa].fa = p;
    calsiz(fa);
    calsiz(p);
}

伸展

Splay（伸展）操作是Splay的核心功能，下面介绍Splay操作的原理。
我们需要讨论以下三种情况：
1. zig/zag式
zig/zag式，即为仅有两个节点，例如：
180301a 1 - Splay原理与实现
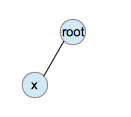
这种情况使用单旋，将儿子变为根。

2.zig-zag式
zig-zag式即儿子-父亲，父亲-祖先的左右儿子关系不相同，如下图。
180301a 2 - Splay原理与实现
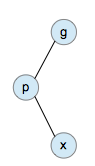
这种情况使用双旋，先转儿子，再转父亲。例如：
原树：
180301a 5 - Splay原理与实现
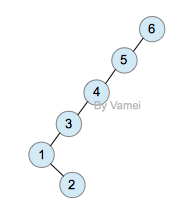
旋转后：
180301a 6 - Splay原理与实现

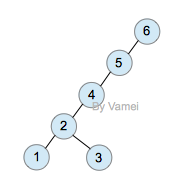
3.zig-zig式
zig-zag式即儿子-父亲，父亲-祖先的左右儿子关系相同，如下图。
180301a 3 - Splay原理与实现
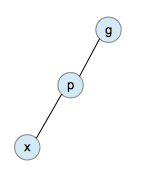
这种情况使用双旋，对儿子进行两次旋转。例如：
180301a 4 - Splay原理与实现
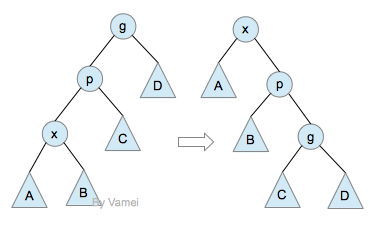
转完以后还是一个链啊？为什么会减小复杂度呢？
试想，既然原树不平衡，说明左侧子树较大，我们把一部分放在右侧，这样就会更平衡。

Splay操作的实现如下。

inline void splay(int p, int tar) {
    for(int fa; (fa = tr[p].fa) != tar; rotate(p)) {
        if(tr[tr[p].fa].fa != tar) {
            rotate(isleft(fa) == isleft(p) ? fa : p);
        }
    }
    if(!tar) rt = p;
}

splay(p, tar)的功能是将p旋转至tar的儿子。

插入/删除

与Treap的操作并无两样，就是需要在插入/删除后splay一下。详情见实现。

inline void insert(int val) {
    if(!rt) {
        rt = newnode();
        tr[rt].val = val;
        tr[rt].siz = tr[rt].cnt = 1;
        return;
    } 
    int p = rt, fa = 0;
    for(;;) {
        if(val == tr[p].val) {
            tr[p].cnt++;
            calsiz(p);
            calsiz(fa);
            splay(p);
            return;
        }
        fa = p;
        p = tr[p].ch[tr[p].val < val];
        if(!p) {
            p = newnode();
            tr[p].val = val;
            tr[p].siz = tr[p].cnt = 1;
            tr[p].fa = fa;
            tr[fa].ch[tr[fa].val < val] = p;
            calsiz(fa);
            splay(p);
            return;
        }
    }
}

inline void delet(int val) {
    queryrk(val);
    if(tr[rt].cnt > 1) {
        tr[rt].cnt--;
        calsiz(rt);
        return;
    }
    if(!tr[rt].ch[0]) {
        delnode(rt);
        rt = tr[rt].ch[1];
        tr[rt].fa = 0;
        return;
    }
    if(!tr[rt].ch[1]) {
        delnode(rt);
        rt = tr[rt].ch[0];
        tr[rt].fa = 0;
        return;
    }
    int ort = rt, lmx = querypre();
    splay(lmx);
    tr[rt].ch[1] = tr[ort].ch[1];
    tr[tr[rt].ch[1]].fa = rt;
    delnode(ort);
    calsiz(rt);
}

其他

其他和Treap区别不大，可以看代码。

区间翻转

将整个数列按照顺序建一棵splay，权值代表数列的第几个数。区间翻转实质上可以通过交换左右儿子实现。而且通过打标记的形式可以做到lazy标记的效果。
在打标记之前，我们首先要把需要翻转的序列放进一个子树中。先splay l-1节点到根，再splay r+1节点到l-1节点儿子处。这样，根的右儿子的左儿子所在子树就是大于l-1小于r+1，即[l, r]区间。在这个子树的根打标记即可。但是要用到l-1和r+1，我们考虑加数列两端加-INF和INF两项，避免l-1和r+1越界。
Splay的中序遍历就是当前数列。

代码

常规操作

这份代码可以通过洛谷【P3369】【模板】普通平衡树（Treap/SBT） – 洛谷或BZOJProblem 3224. — Tyvj 1728 普通平衡树题目。

// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int readint() {
    register int res = 0, neg = 1;
    char c = fgc(); 
    while (c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while (c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

// variable

const int MAXN = 100005, INF = 1e9;

int n, op, x;

// splay

struct Node {
    int ch[2], val, siz, cnt, fa;
} tr[MAXN]; 
int tot = 0, sta[MAXN], stop = 0, rt = 0, anst;

inline void calsiz(int p) {
    tr[p].siz = tr[tr[p].ch[0]].siz + tr[tr[p].ch[1]].siz + tr[p].cnt;
}

inline int newnode() {
    int p;
    if(stop > 0) {
        p = sta[--stop];
    } else {
        p = ++tot;
    } 
    memset(tr + p, 0, sizeof(Node));
    return p;
}

inline void delnode(int a) {
    sta[stop++] = a;
}

inline bool isleft(int p) {
    return tr[tr[p].fa].ch[0] == p;
}

inline void rotate(int p) { // p is child
    bool type = !isleft(p);
    int fa = tr[p].fa, ffa = tr[fa].fa;
    tr[fa].ch[type] = tr[p].ch[!type];
    tr[p].ch[!type] = fa;
    tr[tr[fa].ch[type]].fa = fa;
    if(ffa) tr[ffa].ch[!isleft(fa)] = p;
    tr[p].fa = tr[fa].fa;
    tr[fa].fa = p;
    calsiz(fa);
    calsiz(p);
    if(!tr[p].fa) rt = p;
}

inline void splay(int p) {
    while(tr[p].fa) {
        if(!tr[tr[p].fa].fa) {
            rotate(p);
        } else {
            if(isleft(p) == isleft(tr[p].fa)) {
                rotate(tr[p].fa);
                rotate(p);
            } else {
                rotate(p);
                rotate(p);
            }
        }
    }
}

inline void insert(int val) {
    if(!rt) {
        rt = newnode();
        tr[rt].val = val;
        tr[rt].siz = tr[rt].cnt = 1;
        return;
    } 
    int p = rt, fa = 0;
    for(;;) {
        if(val == tr[p].val) {
            tr[p].cnt++;
            calsiz(p);
            calsiz(fa);
            splay(p);
            return;
        }
        fa = p;
        p = tr[p].ch[tr[p].val < val];
        if(!p) {
            p = newnode();
            tr[p].val = val;
            tr[p].siz = tr[p].cnt = 1;
            tr[p].fa = fa;
            tr[fa].ch[tr[fa].val < val] = p;
            calsiz(fa);
            splay(p);
            return;
        }
    }
}

inline int queryrk(int val) {
    int p = rt, ans = 0;
    for(;;) {
        if(val < tr[p].val) {
            p = tr[p].ch[0];
        } else {
            ans += tr[tr[p].ch[0]].siz;
            if(val == tr[p].val) {
                splay(p);
                return ans + 1;
            } 
            ans += tr[p].cnt;
            p = tr[p].ch[1];
        }
    }
}

inline int queryn(int rk) {
    int p = rt;
    for(;;) {
        if(tr[p].ch[0] && rk <= tr[tr[p].ch[0]].siz) {
            p = tr[p].ch[0];
        } else {
            if(rk <= tr[tr[p].ch[0]].siz + tr[p].cnt) {
                return tr[p].val;
            }
            rk -= tr[tr[p].ch[0]].siz + tr[p].cnt;
            p = tr[p].ch[1];
        }
    }
}

inline int querypre() {
    int p = tr[rt].ch[0];
    while(tr[p].ch[1]) p = tr[p].ch[1];
    return p;
}

inline int querynxt() {
    int p = tr[rt].ch[1];
    while(tr[p].ch[0]) p = tr[p].ch[0];
    return p;
}

inline void delet(int val) {
    queryrk(val);
    if(tr[rt].cnt > 1) {
        tr[rt].cnt--;
        calsiz(rt);
        return;
    }
    if(!tr[rt].ch[0]) {
        delnode(rt);
        rt = tr[rt].ch[1];
        tr[rt].fa = 0;
        return;
    }
    if(!tr[rt].ch[1]) {
        delnode(rt);
        rt = tr[rt].ch[0];
        tr[rt].fa = 0;
        return;
    }
    int ort = rt, lmx = querypre();
    splay(lmx);
    tr[rt].ch[1] = tr[ort].ch[1];
    tr[tr[rt].ch[1]].fa = rt;
    delnode(ort);
    calsiz(rt);
} 

int main() {
    n = readint();
    while(n--) {
        op = readint();
        x = readint();
        switch(op) {
            case 1:
                insert(x);
                break;
            case 2:
                delet(x);
                break;
            case 3:
                printf("%d\n", queryrk(x));
                break;
            case 4:
                printf("%d\n", queryn(x));
                break;
            case 5:
                insert(x);
                printf("%d\n", tr[querypre()].val);
                delet(x);
                break;
            case 6:
                insert(x);
                printf("%d\n", tr[querynxt()].val);
                delet(x);
                break; 
        } 
    }
    return 0;
}

区间翻转

这份代码可以通过洛谷【P3391】【模板】文艺平衡树（Splay） – 洛谷或BZOJProblem 3223. — Tyvj 1729 文艺平衡树题目。

// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <algorithm>

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int readint() {
    register int res = 0, neg = 1;
    char c = fgc(); 
    while (c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while (c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

// variable

const int MAXN = 100005, INF = 1e9;

int n, m, ll, rr, data[MAXN];

// splay

struct Node {
    int ch[2], val, siz, cnt, fa;
    bool tag;
} tr[MAXN]; 
int tot = 0, sta[MAXN], stop = 0, rt = 0;

inline void calsiz(int p) {
    tr[p].siz = tr[tr[p].ch[0]].siz + tr[tr[p].ch[1]].siz + tr[p].cnt;
}

inline int newnode() {
    int p;
    if(stop > 0) {
        p = sta[--stop];
    } else {
        p = ++tot;
    } 
    memset(tr + p, 0, sizeof(Node));
    return p;
}

inline void delnode(int a) {
    sta[stop++] = a;
}

inline bool isleft(int p) {
    return tr[tr[p].fa].ch[0] == p;
}

inline void rotate(int p) { // p is child
    bool type = !isleft(p);
    int fa = tr[p].fa, ffa = tr[fa].fa;
    tr[fa].ch[type] = tr[p].ch[!type];
    tr[p].ch[!type] = fa;
    tr[tr[fa].ch[type]].fa = fa;
    if(ffa) tr[ffa].ch[!isleft(fa)] = p;
    tr[p].fa = tr[fa].fa;
    tr[fa].fa = p;
    calsiz(fa);
    calsiz(p);
}

inline void splay(int p, int tar) {
    for(int fa; (fa = tr[p].fa) != tar; rotate(p)) {
        if(tr[tr[p].fa].fa != tar) {
            rotate(isleft(fa) == isleft(p) ? fa : p);
        }
    }
    if(!tar) rt = p;
}

inline void pushdown(int p) {
    if(tr[p].tag) {
        if(tr[p].ch[0]) tr[tr[p].ch[0]].tag = !tr[tr[p].ch[0]].tag;
        if(tr[p].ch[1]) tr[tr[p].ch[1]].tag = !tr[tr[p].ch[1]].tag;
        std::swap(tr[p].ch[0], tr[p].ch[1]);
        tr[p].tag = false;
    }
}

inline int queryn(int rk) {
    int p = rt;
    for(;;) {
        pushdown(p);
        if(tr[p].ch[0] && rk <= tr[tr[p].ch[0]].siz) {
            p = tr[p].ch[0];
        } else {
            if(rk <= tr[tr[p].ch[0]].siz + tr[p].cnt) {
                return p;
            }
            rk -= tr[tr[p].ch[0]].siz + tr[p].cnt;
            p = tr[p].ch[1];
        }
    }
}

inline int build(int fa, int l, int r) {
    if(l > r) return 0;
    int mid = (l + r) >> 1, p = newnode();
    tr[p].val = data[mid];
    tr[p].fa = fa;
    tr[p].ch[0] = build(p, l, mid - 1);
    tr[p].ch[1] = build(p, mid + 1, r);
    tr[p].cnt = 1;
    calsiz(p);
    return p;
}

inline void reverse(int l, int r) {
    int x = queryn(l), y = queryn(r + 2);
    splay(x, 0);
    splay(y, x);
    tr[tr[tr[rt].ch[1]].ch[0]].tag = !tr[tr[tr[rt].ch[1]].ch[0]].tag;
}

inline void dfs(int p) {
    pushdown(p);
    if(tr[p].ch[0]) dfs(tr[p].ch[0]);
    if(tr[p].val != -INF && tr[p].val != INF) {
        printf("%d ", tr[p].val);
    }
    if(tr[p].ch[1]) dfs(tr[p].ch[1]);
}

int main() {
    n = readint();
    m = readint();
    for(int i = 2; i <= n + 1; i++) {
        data[i] = i - 1;
    }
    data[1] = -INF;
    data[n + 2] = INF;
    rt = build(0, 1, n + 2);
    while(m--) {
        ll = readint();
        rr = readint();
        reverse(ll, rr);
    }
    dfs(rt);
    return 0;
}

参考资料

文中图片也来源于参考资料。

Author:
Filed Under: 算法, 知识, Slider
Tags: , ,

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

此站点使用Akismet来减少垃圾评论。了解我们如何处理您的评论数据。