题目地址：洛谷：【P1117】[NOI2016]优秀的拆分 – 洛谷、BZOJ：Problem 4650. — [Noi2016]优秀的拆分

题目描述

如果一个字符串可以被拆分为 AABB 的形式，其中 A和 B是任意非空字符串，则我们称该字符串的这种拆分是优秀的。
例如，对于字符串 aabaabaa，如果令 A=aab，B=a，我们就找到了这个字符串拆分成 AABB的一种方式。
一个字符串可能没有优秀的拆分，也可能存在不止一种优秀的拆分。比如我们令 A=a，B=baa，也可以用 AABB表示出上述字符串；但是，字符串 abaabaa 就没有优秀的拆分。
现在给出一个长度为 n的字符串 S，我们需要求出，在它所有子串的所有拆分方式中，优秀拆分的总个数。这里的子串是指字符串中连续的一段。
以下事项需要注意：

1. 出现在不同位置的相同子串，我们认为是不同的子串，它们的优秀拆分均会被记入答案。
2. 在一个拆分中，允许出现 A=B。例如 cccc 存在拆分 A=B=c。
3. 字符串本身也是它的一个子串。

题意简述

问一个字符串所有子串中，能够将子串拆分成AABB的拆分方案总数。其中A、B是任意非空串，A=B同样合法。

输入输出格式

输入格式：
每个输入文件包含多组数据。输入文件的第一行只有一个整数 T，表示数据的组数。保证 1≤T≤10。
接下来 T行，每行包含一个仅由英文小写字母构成的字符串 S，意义如题所述。

输出格式：
输出 T行，每行包含一个整数，表示字符串 S 所有子串的所有拆分中，总共有多少个是优秀的拆分。

输入输出样例

输入样例#1：

4
aabbbb
cccccc
aabaabaabaa
bbaabaababaaba

输出样例#1：

3
5
4
7

说明

我们用 S[i,j]表示字符串 S第 i 个字符到第 j个字符的子串（从 1开始计数）。
第一组数据中，共有 3个子串存在优秀的拆分：
S[1,4]=aabb，优秀的拆分为 A=a，B=b；
S[3,6]=bbbb，优秀的拆分为 A=b，B=b；
S[1,6]=aabbbb，优秀的拆分为 A=a，B=bb。
而剩下的子串不存在优秀的拆分，所以第一组数据的答案是 3。
第二组数据中，有两类，总共 4 个子串存在优秀的拆分：
对于子串 S[1,4]=S[2,5]=S[3,6]=cccc，它们优秀的拆分相同，均为 A=c，B=c，但由于这些子串位置不同，因此要计算 3 次；
对于子串 S[1,6]=cccccc，它优秀的拆分有 2 种：A=c，B=cc 和 A=cc，B=c，它们是相同子串的不同拆分，也都要计入答案。
所以第二组数据的答案是 3+2=5。
第三组数据中，S[1,8] 和 S[4,11] 各有 2 种优秀的拆分，其中 S[1,8] 是问题描述中的例子，所以答案是 2+2=4。
第四组数据中，S[1,4]，S[6,11]，S[7,12]，S[2,11]，S[1,8] 各有 1种优秀的拆分，S[3,14] 有 2 种优秀的拆分，所以答案是 5+2=7。
对于全部的测试点,保证 1≤T≤10。以下对数据的限制均是对于单组输入数据而言的，也就是说同一个测试点下的 T组数据均满足限制条件。
我们假定 n 为字符串 S 的长度，每个测试点的详细数据范围见下表：
All n≤30000

题解

参考资料：

• NOI2016 优秀的拆分（图解） – CSDN博客
• NOI2016优秀的拆分 后缀数组 – CSDN博客
• BZOJ4650 : [Noi2016]优秀的拆分 – Claris – 博客园

我们考虑对于每个位置i，统计两个信息pre和suf，表示前缀i后缀为AA的个数与后缀i前缀为AA的个数。答案显然就是 \displaystyle \sum_{i=1}^n pre[i]suf[i+1]。
后缀的前缀和前缀的后缀问题显然可以用SA解决（方法参见：后缀数组（倍增）算法原理及应用 | KSkun’s Blog），但是我们需要一个统计的思路。
考虑枚举AA模式中一段A的串长k，然后在原串中每k个字符设置一个关键点，对于任意一个A串长为k的AA串，一定恰好经过两个相邻的关键点kt、k(t+1)。我们考虑求出两关键点的前缀LCS长度l和后缀LCP长度r，如果 (l+r) \geq k，则我们就找到了一个符合条件的AA串。

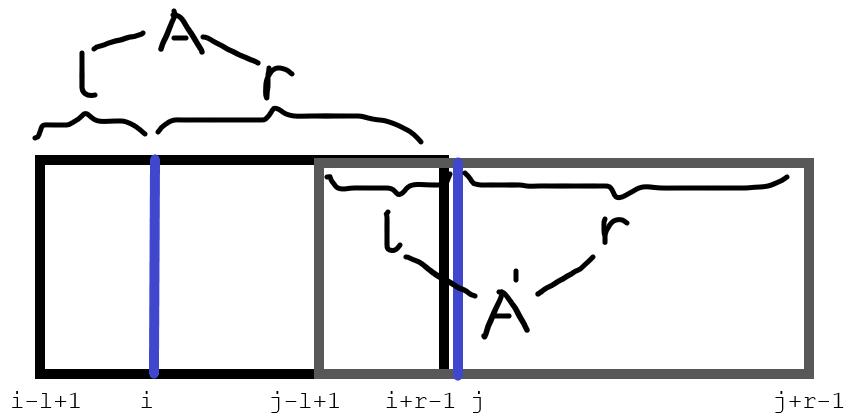
考虑找到的每个AA串对pre和suf造成的影响。设相邻的两个关键点靠前的为i，靠后的为j。能够产生AA串作为前缀的位置，这一段位置应当是[j-l+k, j+r-1]。对应示例图，我们可以发现这段区间对应的是A’这个串第k个字符到末尾，这是由于A部分此时至少要保留[i-l+1, j-l-1]这一段，也就对应A’部分的[i-l+k+1, j-l+k-1]一段。而作为后缀的位置是[i-l+1, i+r-k]，原理相同。那么实际上每次的操作就是对pre、suf中连续一段区间+1，可以将操作差分降低复杂度。
这样一通操作下来的复杂度实际上是O(Tn \log n)的，数据范围不是很卡。

代码

// Code by KSkun, 2018/5
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>

typedef long long LL;

const int MAXN = 100005;

int Log2[MAXN];

inline void callog2() {
    for(int i = 2; i < MAXN; i++) {
        Log2[i] = Log2[i >> 1] + 1;
    }
}

struct SuffixArray {
    char s[MAXN];
    int n, m, sa[MAXN], t[MAXN], t1[MAXN], c[MAXN], rnk[MAXN], hei[MAXN], st[MAXN][25];
    inline void init() {
        memset(this, 0, sizeof(SuffixArray));
    }
    inline void calsa() {
        int *x = t, *y = t1;
        for(int i = 1; i <= m; i++) c[i] = 0;
        for(int i = 1; i <= n; i++) c[x[i] = s[i]]++;
        for(int i = 1; i <= m; i++) c[i] += c[i - 1];
        for(int i = n; i >= 1; i--) sa[c[x[i]]--] = i;
        for(int k = 1; k <= n; k <<= 1) {
            int p = 0;
            for(int i = n - k + 1; i <= n; i++) y[++p] = i;
            for(int i = 1; i <= n; i++) if(sa[i] > k) y[++p] = sa[i] - k;
            for(int i = 1; i <= m; i++) c[i] = 0;
            for(int i = 1; i <= n; i++) c[x[y[i]]]++;
            for(int i = 1; i <= m; i++) c[i] += c[i - 1];
            for(int i = n; i >= 1; i--) sa[c[x[y[i]]]--] = y[i];
            std::swap(x, y);
            p = x[sa[1]] = 1;
            for(int i = 2; i <= n; i++) {
                x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k]) 
                    ? p : ++p;
            }
            if(p >= n) break;
            m = p;
        }
        memcpy(rnk, x, sizeof(rnk));
        int k = 0;
        for(int i = 1; i <= n; i++) {
            int j = sa[rnk[i] + 1];
            if(k) k--;
            if(!j) continue;
            while(s[i + k] == s[j + k]) k++;
            hei[rnk[i]] = k;
        }
    }
    inline void calst() {
        for(int i = 1; i <= n; i++) {
            st[i][0] = hei[i];
        }
        for(int i = 1; i <= 20; i++) {
            for(int j = 1; j + (1 << i) <= n; j++) {
                st[j][i] = std::min(st[j][i - 1], st[j + (1 << (i - 1))][i - 1]);
            }
        }
    }
    inline int querylcp(int x, int y) {
        x = rnk[x]; y = rnk[y];
        if(x > y) std::swap(x, y);
        int t = Log2[y - x];
        return std::min(st[x][t], st[y - (1 << t)][t]);
    }
} saa, sab;

int T, n, pre[MAXN], suf[MAXN];

inline int lcp(int x, int y) {
    return saa.querylcp(x, y);
}

inline int lcs(int x, int y) {
    return sab.querylcp(n - x + 1, n - y + 1);
}

int main() {
    callog2();
    scanf("%d", &T);
    while(T--) {
        saa.init(); sab.init();
        memset(pre, 0, sizeof(pre));
        memset(suf, 0, sizeof(suf));
        saa.m = sab.m = 256;
        scanf("%s", saa.s + 1);
        saa.n = sab.n = n = strlen(saa.s + 1);
        for(int i = 1; i <= n; i++) {
            sab.s[i] = saa.s[n - i + 1];
        }
        saa.calsa(); saa.calst();
        sab.calsa(); sab.calst();
        for(int k = 1; k <= n >> 1; k++) {
            for(int i = k, j = i + k; j <= n; i += k, j += k) {
                int l = std::min(lcs(i - 1, j - 1), k - 1), r = std::min(lcp(i, j), k);
                if(l + r >= k) {
                    pre[j - l + k - 1]++; pre[j + r]--;
                    suf[i - l]++; suf[i + r - k + 1]--;
                }
            }
        }
        for(int i = 1; i <= n; i++) {
            pre[i] += pre[i - 1];
            suf[i] += suf[i - 1];
        }
        LL ans = 0;
        for(int i = 1; i <= n; i++) {
            ans += 1ll * pre[i] * suf[i + 1];
        }
        printf("%lld\n", ans);
    }
    return 0;
}