概述

我们在做运动学图像题的时候总是会面临一些非传统的运动学图像，在这篇文章中，我将归总我遇到过的有趣的创新图像题以及分析方法。

模型与例题

$a-x$图像或$x-a$图像

例题

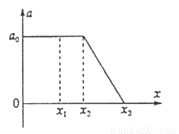
（多选）放在水平面上的物体，在水平力$F$作用下开始运动，以物体静止时的位置为坐标原点，力$F$的方向为正方向建立$x$轴，物体的加速度随位移的变化图像如图所示。下列说法中错误的是

A. 位移为$x_1$时，物体的速度大小为$\sqrt{2a_0x_1}$
B. 位移为$x_2$时，物体的速度达到最大
C. 物体的最大速度为$\sqrt{a_0(x_2+x_3)}$
D. $0 \sim x_2$过程中物体做匀加速直线运动，$x_2 \sim x_3$过程中物体做匀减速直线运动

题目来源：放在水平面上的物体，在水平力F作用下开始运动，以物体静止时的位置为坐标原点，力F的方向为正方向建立x轴，物体的加速度随位移的变化图像如图所示… 满分5满分网

【解析】

本题给了一个$a-x$图像。我们注意到，在$x_2 \sim x_3$段的图像是一条直线，这是随时间增大均匀减小的加速度吗？显然不是。

在与计算无关的情况下，我们可以认为$x$轴就是原来$a-t$图像的$t$轴，只是这根轴上的数值分布不均匀。用这种方法可以定性分析运动的相关情况。我们发现，在整个运动中物体都在加速。
在需要计算的情况下，我们显然无法使用观察图像的方法获得速度的变化量。对于这个图像，我们能使用的公式只有$v_t^2 – v_0^2 = 2ax$这一个了。然而用好它也能解决很多问题。

接下来我们逐选项地分析题目。
A项，在$x_1$处使用公式$v_1^2 – 0 = 2a_0x_1$，即可求出$v_1=\sqrt{2a_0x_1}$，本项是正确的。
B项，由于全段都在加速，$x_3$才是速度达到最大的时候的位移值。
C项，最大速度显然要计算$x_3$处的速度$v_3$，但是问题来了，这是一个变加速直线运动，我们无法利用传统方法求解了，还有什么其他的办法呢？观察公式$v^2=2ax$，$ax$不就是图形的面积吗？我们可以求出图形的面积为$S=\frac12(x_2+x_3)a_0$，代入上面的公式，得到了我们要求的速度$v_3^2=(x_2+x_3)a_0$，即$v_3=\sqrt{(x_2+x_3)a_0}$。
D项，$x_2 \sim x_3$段加速度恒为正，物体在做匀加速运动。
最后还有一个坑，题目要求选出错误的，因此应该选择BD两项。

本题解决非传统问题的方法是，通过公式得到非传统图像的面积意义，从而解决非传统问题。看来，对于图像与公式的意义把握是解决问题的重要手段。

$v-x$图像或$x-v$图像

例题

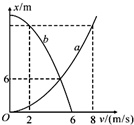
（多选）甲、乙两质点在同一时刻、同一地点沿同一方向做直线运动。质点甲做初速度为零，加速度大小为$a_1$的匀加速直线运动。质点乙做初速度为$v_0$，加速度大小为$a_2$的匀减速直线运动至速度减为零保持静止。甲、乙两质点在运动过程中的$x-v$（位置速度）图象如图所示（虚线与对应的坐标轴垂直）。则

A. 在$x-v$图象中，图线$a$表示质点甲的运动，质点乙的初速度$v_0=6 \ \mathrm{m/s}$
B. 质点乙的加速度大小$a_2=2 \ \mathrm{m/s^2}$
C. 质点甲的加速度大小$a_1=2 \ \mathrm{m/s^2}$
D. 图线$a$、$b$的交点表示两质点同时到达同一位置

题目来源：【甲、乙两质点在同一时刻、同一地点沿同一方向做直线运动．质点甲做初速度为零，加速度大小为a1的匀加速直线运动．质点乙做初速度为v0，加速度大小为a2的匀减速直线运动至速度减为零】作业帮

【解析】

这又是一个不按套路来的题目，我们习惯了看$x-t$图像以后看这个怎么看怎么不舒服，于是就容易做错。不过由于可以通过图像推导出一些常规结论，相比需要利用图形面积意义的题目还是要简单些。

A项，容易知两物体都是从$x=0$位置开始运动，由于乙有初速度，因此乙对应图线$b$，甲对应$a$。查起始位置处速度得知$v_{0}=6 \ \mathrm{m/s}$。
B项与C项，这样的图线应当如何计算加速度成为了一个问题。计算的困难来自于图形的关键点都只给了半边信息，有横坐标信息的关键点没给纵坐标，有纵坐标的没给横坐标，不过不要虚，要相信题是能做出来的，我们按部就班地来准备方程：
不妨关注共速的位置，假设二者共同速度为$v$：
对甲：
$$ v^2 = 2a_1x \tag{1}$$
对乙：
$$ v_0^2 – v^2 = 2a_2x \tag{2} $$
联立(1)式和(2)式，得到$a_1+a_2=3 \ \mathrm{m/s^2} \tag{*1}$
我们再取一个共位移的位置，此时$v_1=8 \ \mathrm{m/s}$，$v_2=2 \ \mathrm{m/s}$，假设二者位移都是$x$：
对甲：
$$ v_1^2 = 2a_1x \tag{3} $$
对乙：
$$ v_0^2 – v_2^2 = 2a_2x \tag{4} $$
联立(3)和(4)，得到$a_1=2a_2 \tag{*2}$
到此为止，我们已经可以通过(*1)和(*2)得到答案为$a_1=2 \ \mathrm{m/s^2}, a_2=1 \ \mathrm{m/s^2}$。从而判断C正确，B错误。
对于D项，交点表示两物体的速度相同且位移相同的一个状态，但是不一定要同时达到，基于数据的分析也可以证明确实不是同时达到的。

我们可以发现，给半边条件也是有用的，因为有两个物体，每个物体列出一个式子，设一个未知数，就可以在两个式子间消元获得足够的信息了。

假设运动法

例题

研究人员测得飞机着陆后若不制动在平直跑道上滑行的总距离为$x$，所用的时间为$t$。考虑到飞机的滑行速度越小，所受的阻力越小，则飞机着陆时的速度应为
A. $v < \frac{x}{t}$
B. $\frac{x}{t} < v < \frac{2x}{t}$
C. $v = \frac{2x}{t}$
D. $v > \frac{2x}{t}$

题目来源：《高考小题练透 物理》（67高考，外研社）、【某同学欲估算飞机着陆时的速度，他假设飞机在平直跑道上做匀减速运动，飞机在跑道上滑行的距离为x，从着陆到停下来所用的时间为t，实际上，飞机的速度越大，所受的阻力越大，即加】作业帮

【解析】

由于阻力随滑行速度减小而减小，减速的加速度大小是在减小的，因此$v-t$图像看上去应该是下凸的，这就给我们估计$t=0$时的速度带来了麻烦，毕竟我们并不知道它和平均速度的关系。

为了解决这个问题，我们不妨假设一个在$t$时间内的匀减速运动，并把图像和题目中这个运动的图像做到一起，观察我们将得到什么。

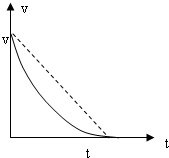
这个匀减速运动的平均速度显然是$\frac{v}{2}$，而题目中这个运动的位移是小于匀减速运动的，因此平均速度也要小于匀减速的，即$\frac{x}{t} < \frac{v}{2}$，便推知了$v > \frac{2x}{t}$这一结论。

有的运动我们并不熟悉，也不好用已有的运动学手段甚至是数学手段来处理它的（图像）问题，我们可以利用与上面类似的“假设”思想发现新的突破口。