注：本文部分图片来自互联网，其相关权利归原作者所有，感谢原作者的分享。

概述

Treap是一种改进的BST（二叉查找树，Binary Search Tree）平衡树，Treap的命名来自于Tree+Heap，其旋转的依据是节点随机权值满足堆序性。通常我们将其规定为小根堆。Treap是常见的平衡树的种类。

原理与实现

我们用结构体Node存放平衡树每个节点的信息，下面是Node的实现。

struct Node {
    int lch, rch, val, rnd, siz, cnt;
    // 从左到右依次是左儿子，右儿子，节点值，随机权值，子树大小，这个数的出现次数
} treap[MAXN]; 

旋转

旋转是Treap的基本操作之一。Treap的旋转分为左旋和右旋两种，如下图所示。

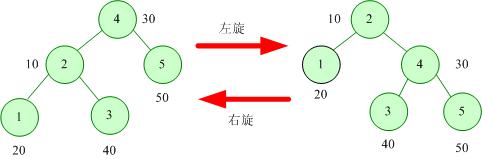
右旋指将左儿子提到根，将根向下移动到右儿子。左旋是右旋的相反操作。这两种操作有助于保证树的平衡。至于旋转后是否满足堆序性，看旋转操作的过程就可以证明。
下面是左旋和右旋的实现。

inline void lrotate(int &a) {
    int b = treap[a].rch;
    treap[a].rch = treap[b].lch;
    treap[b].lch = a;
    treap[b].siz = treap[a].siz;
    calsiz(a);
    a = b;
}

inline void rrotate(int &a) {
    int b = treap[a].lch;
    treap[a].lch = treap[b].rch;
    treap[b].rch = a;
    treap[b].siz = treap[a].siz;
    calsiz(a);
    a = b;
}

旋转完毕后，a的值就是新的根。

插入

插入的操作如图所示。

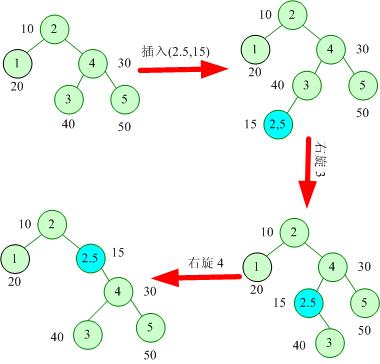
先按照BST的性质（比当前节点的数小的都在左子树，否则在右子树）找到需要插入的位置，然后新建节点放进去。此时，如果发现左右儿子有不满足堆序性的情况，将其旋转至满足堆序性。
下面是插入操作的实现。

inline void insert(int &p, int val) {
    if(!p) {
        p = newnode();
        treap[p].val = val;
        treap[p].rnd = rand();
        treap[p].siz = treap[p].cnt = 1;
        return;
    }
    treap[p].siz++;
    if(treap[p].val == val) {
        treap[p].cnt++;
    } else if(treap[p].val > val) {
        insert(treap[p].lch, val);
        if(treap[treap[p].lch].rnd < treap[p].rnd) rrotate(p); 
    } else {
        insert(treap[p].rch, val);
        if(treap[treap[p].rch].rnd < treap[p].rnd) lrotate(p); 
    }
}

插入操作完成后p会修改为树根。

删除

删除的操作如图所示。

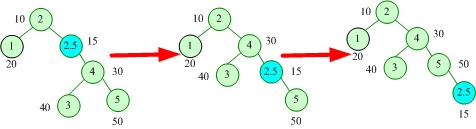
删除操作首先找到这个要删的点，如果出现次数超过1次直接删出现次数即可。否则需要删除这个点，把这个点转到至多有一棵子树的位置，然后将子树接上来，直接删除即可。
下面是删除操作的实现。

inline void delet(int &p, int val) {
    if(!p) return;
    if(treap[p].val == val) {
        if(treap[p].cnt > 1) {
            treap[p].cnt--;
            treap[p].siz--;
        } else if(!treap[p].lch) {
            delnode(p);
            p = treap[p].rch;
        } else if(!treap[p].rch) {
            delnode(p);
            p = treap[p].lch;
        } else {
            if(treap[treap[p].lch].rnd < treap[treap[p].rch].rnd) {
                rrotate(p);
                delet(p, val);
            } else {
                lrotate(p);
                delet(p, val);
            }
        }  
        return;
    }
    if(treap[p].val > val) {
        treap[p].siz--;
        delet(treap[p].lch, val);
    } else {
        treap[p].siz--;
        delet(treap[p].rch, val); 
    }
}

应用：查询一个数的排名

判断当前节点与查询数的大小关系
大→找左子树
相等→答案为左子树大小+1
小→找右子树，然后加上左子树大小和当前节点出现次数
下面是实现。

inline int queryrk(int p, int val) {
    if(!p) return 0;
    if(treap[p].val == val) return treap[treap[p].lch].siz + 1;
    else if(treap[p].val > val) return queryrk(treap[p].lch, val);
    else return queryrk(treap[p].rch, val) + treap[treap[p].lch].siz + treap[p].cnt;
}

应用：查询排名为某的数

当前节点左子树不大于查询排名→找左子树
查询排名大于当前节点左子树+当前节点出现次数→找右子树
否则→这个数就是我们要找的
下面是实现。

inline int queryn(int p, int rk) {
    if(!p) return 0;
    if(treap[treap[p].lch].siz >= rk) return queryn(treap[p].lch, rk);
    else if(treap[treap[p].lch].siz + treap[p].cnt < rk) return queryn(treap[p].rch, rk - treap[treap[p].lch].siz - treap[p].cnt);
    else return treap[p].val;
}

应用：查询一个数的前驱（不大于这个数的最大数）

当前节点小了→更新答案，找右子树
当前节点大了→找左子树

inline void querypre(int p, int val) {
    if(!p) return;
    if(treap[p].val < val) {
        anst = p;
        querypre(treap[p].rch, val);
    } else return querypre(treap[p].lch, val);
}

应用：查询一个数的后继（不小于这个数的最小数）

与上面的查询相似。

inline void querynxt(int p, int val) {
    if(!p) return;
    if(treap[p].val > val) {
        anst = p;
        querynxt(treap[p].lch, val);
    } else return querynxt(treap[p].rch, val);
}

代码

这份代码可以通过洛谷【P3369】【模板】普通平衡树（Treap/SBT） – 洛谷或BZOJProblem 3224. — Tyvj 1728 普通平衡树（BZOJ不能使用ctime库）题目。

// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <ctime>

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int readint() {
    register int res = 0, neg = 1;
    char c = fgc(); 
    while (c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while (c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

// variable

const int MAXN = 100005, INF = 1e9;

int n, op, x;

// treap

struct Node {
    int lch, rch, val, rnd, siz, cnt;
} treap[MAXN]; 
int tot = 0, sta[MAXN], stop = 0, rt = 0, anst;

inline void calsiz(int p) {
    treap[p].siz = treap[treap[p].lch].siz + treap[treap[p].rch].siz + treap[p].cnt;
}

inline int newnode() {
    int p;
    if(stop > 0) {
        p = sta[--stop];
    } else {
        p = ++tot;
    } 
    memset(treap + p, 0, sizeof(Node));
    return p;
}

inline void delnode(int a) {
    sta[stop++] = a;
}

inline void lrotate(int &a) {
    int b = treap[a].rch;
    treap[a].rch = treap[b].lch;
    treap[b].lch = a;
    treap[b].siz = treap[a].siz;
    calsiz(a);
    a = b;
}

inline void rrotate(int &a) {
    int b = treap[a].lch;
    treap[a].lch = treap[b].rch;
    treap[b].rch = a;
    treap[b].siz = treap[a].siz;
    calsiz(a);
    a = b;
}

inline void insert(int &p, int val) {
    if(!p) {
        p = newnode();
        treap[p].val = val;
        treap[p].rnd = rand();
        treap[p].siz = treap[p].cnt = 1;
        return;
    }
    treap[p].siz++;
    if(treap[p].val == val) {
        treap[p].cnt++;
    } else if(treap[p].val > val) {
        insert(treap[p].lch, val);
        if(treap[treap[p].lch].rnd < treap[p].rnd) rrotate(p); 
    } else {
        insert(treap[p].rch, val);
        if(treap[treap[p].rch].rnd < treap[p].rnd) lrotate(p); 
    }
}

inline void delet(int &p, int val) {
    if(!p) return;
    if(treap[p].val == val) {
        if(treap[p].cnt > 1) {
            treap[p].cnt--;
            treap[p].siz--;
        } else if(!treap[p].lch) {
            delnode(p);
            p = treap[p].rch;
        } else if(!treap[p].rch) {
            delnode(p);
            p = treap[p].lch;
        } else {
            if(treap[treap[p].lch].rnd < treap[treap[p].rch].rnd) {
                rrotate(p);
                delet(p, val);
            } else {
                lrotate(p);
                delet(p, val);
            }
        }  
        return;
    }
    if(treap[p].val > val) {
        treap[p].siz--;
        delet(treap[p].lch, val);
    } else {
        treap[p].siz--;
        delet(treap[p].rch, val); 
    }
}

inline int queryrk(int p, int val) {
    if(!p) return 0;
    if(treap[p].val == val) return treap[treap[p].lch].siz + 1;
    else if(treap[p].val > val) return queryrk(treap[p].lch, val);
    else return queryrk(treap[p].rch, val) + treap[treap[p].lch].siz + treap[p].cnt;
}

inline int queryn(int p, int rk) {
    if(!p) return 0;
    if(treap[treap[p].lch].siz >= rk) return queryn(treap[p].lch, rk);
    else if(treap[treap[p].lch].siz + treap[p].cnt < rk) return queryn(treap[p].rch, rk - treap[treap[p].lch].siz - treap[p].cnt);
    else return treap[p].val;
}

inline void querypre(int p, int val) {
    if(!p) return;
    if(treap[p].val < val) {
        anst = p;
        querypre(treap[p].rch, val);
    } else return querypre(treap[p].lch, val);
}

inline void querynxt(int p, int val) {
    if(!p) return;
    if(treap[p].val > val) {
        anst = p;
        querynxt(treap[p].lch, val);
    } else return querynxt(treap[p].rch, val);
}

int main() {
    srand(time(NULL));
    n = readint();
    while(n--) {
        op = readint();
        x = readint();
        switch(op) {
            case 1:
                insert(rt, x);
                break;
            case 2:
                delet(rt, x);
                break;
            case 3:
                printf("%d\n", queryrk(rt, x));
                break;
            case 4:
                printf("%d\n", queryn(rt, x));
                break;
            case 5:
                anst = 0;
                querypre(rt, x);
                printf("%d\n", treap[anst].val);
                break;
            case 6:
                anst = 0;
                querynxt(rt, x);
                printf("%d\n", treap[anst].val);
                break; 
        } 
    }
    return 0;
}