[SDOI2009]晨跑 题解
题目地址:洛谷:【P2153】[SDOI2009]晨跑 – 洛谷、BZOJ:P …
May all the beauty be blessed.
题目地址:洛谷:【P3227】[HNOI2013]切糕 – 洛谷、BZOJ:Problem 3144. — [Hnoi2013]切糕
经过千辛万苦小 A 得到了一块切糕,切糕的形状是长方体,小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑,小 A 希望切面能尽量光滑且和谐。于是她找到你,希望你能帮她找出最好的切割方案。
出于简便考虑,我们将切糕视作一个长 P、宽 Q、高 R 的长方体点阵。我们将位于第 z层中第 x 行、第 y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z),它有一个非负的不和谐值 v(x,y,z)。一个合法的切面满足以下两个条件:
输入格式:
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1<=x<=P, 1<=y<=Q, 1<=z<=R)。
100%的数据满足P,Q,R<=40,0<=D<=R,且给出的所有的不和谐值不超过1000。
输出格式:
仅包含一个整数,表示在合法基础上最小的总不和谐值。
输入样例#1:
2 2 2 1 6 1 6 1 2 6 2 6
输出样例#1:
6
最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1
网络流中,表示“选择”含义我们通常使用最小割模型。本题中,我们想从某个纵轴(x, y)的若干点中选取一个,这种情况我们可以采取用点权作为容量的边将点连成一条链,再分别从链头链尾向源汇连不可割(容量无限)的边,这样割去某个边就可以代表选择某个点了。
然后,我们还需要加入限制|f(x,y)-f(x',y')| \leq D。其实就是说,对于每个点,当相邻纵轴选取的点的距离超过D,就得让这种方案无效,即仍然有流可以通过这一部分到达汇,可以通过加边的方法实现。对于任意点 (x, y, z) ,向相邻点 (x', y', z - D) 连容量无限的边,这样就可以满足限制条件了。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005, INF = 1e9;
struct Edge {
int to, cap, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap) {
gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, head[v]}; head[v] = tot++;
}
int level[MAXN];
inline bool bfs(int s, int t) {
memset(level, -1, sizeof(level));
std::queue<int> que;
level[s] = 0; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop();
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == -1) {
level[v] = level[u] + 1;
if(v == t) return true;
que.push(v);
}
}
}
return level[t] != -1;
}
int cur[MAXN];
inline int dfs(int u, int t, int left) {
if(u == t || !left) return left;
int flow = 0;
for(int &i = cur[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && level[v] == level[u] + 1) {
int d = dfs(v, t, std::min(left, gra[i].cap));
if(d > 0) {
flow += d; left -= d;
gra[i].cap -= d; gra[i ^ 1].cap += d;
if(!left) return flow;
}
}
}
return flow;
}
inline int dinic(int s, int t) {
int flow = 0;
while(bfs(s, t)) {
memcpy(cur, head, sizeof(head));
int f;
while(f = dfs(s, t, INF)) {
flow += f;
}
}
return flow;
}
const int fix[2][4] = {{1, -1, 0, 0}, {0, 0, 1, -1}};
int n, m, h, d, v[45][45][45], S, T;
int main() {
memset(head, -1, sizeof(head));
n = readint(); m = readint(); h = readint(); d = readint();
S = n * m * (h + 1) + 1; T = S + 1;
for(int k = 1; k <= h; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
v[i][j][k] = readint();
}
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
int p = (i - 1) * m + j;
addedge(S, p, INF);
addedge(h * n * m + p, T, INF);
for(int k = 1; k <= h; k++) {
addedge((k - 1) * n * m + p, k * n * m + p, v[i][j][k]);
}
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
for(int t = 0; t < 4; t++) {
int nx = i + fix[0][t], ny = j + fix[1][t];
if(nx < 1 || nx > n || ny < 1 || ny > m) continue;
for(int k = d + 1; k <= h + 1; k++) {
addedge((k - 1) * n * m + (i - 1) * m + j,
(k - d - 1) * n * m + (nx - 1) * m + ny, INF);
}
}
}
}
printf("%d", dinic(S, T));
return 0;
}
题目地址:洛谷:【P4249】[WC2007]剪刀石头布 – 洛谷、BZOJ:Problem 2597. — [Wc2007]剪刀石头布
在一些一对一游戏的比赛(如下棋、乒乓球和羽毛球的单打)中,我们经常会遇到A胜过B,B胜过C而C又胜过A的有趣情况,不妨形象的称之为剪刀石头布情况。有的时候,无聊的人们会津津乐道于统计有多少这样的剪刀石头布情况发生,即有多少对无序三元组(A, B, C),满足其中的一个人在比赛中赢了另一个人,另一个人赢了第三个人而第三个人又胜过了第一个人。注意这里无序的意思是说三元组中元素的顺序并不重要,将(A, B, C)、(A, C, B)、(B, A, C)、(B, C, A)、(C, A, B)和(C, B, A)视为相同的情况。
有N个人参加一场这样的游戏的比赛,赛程规定任意两个人之间都要进行一场比赛:这样总共有场比赛。比赛已经进行了一部分,我们想知道在极端情况下,比赛结束后最多会发生多少剪刀石头布情况。即给出已经发生的比赛结果,而你可以任意安排剩下的比赛的结果,以得到尽量多的剪刀石头布情况。
输入格式:
输入文件的第1行是一个整数N,表示参加比赛的人数。
之后是一个N行N列的数字矩阵:一共N行,每行N列,数字间用空格隔开。
在第(i+1)行的第j列的数字如果是1,则表示i在已经发生的比赛中赢了j;该数字若是0,则表示在已经发生的比赛中i败于j;该数字是2,表示i和j之间的比赛尚未发生。数字矩阵对角线上的数字,即第(i+1)行第i列的数字都是0,它们仅仅是占位符号,没有任何意义。
输入文件保证合法,不会发生矛盾,当i≠j时,第(i+1)行第j列和第(j+1)行第i列的两个数字要么都是2,要么一个是0一个是1。
输出格式:
输出文件的第1行是一个整数,表示在你安排的比赛结果中,出现了多少剪刀石头布情况。
输出文件的第2行开始有一个和输入文件中格式相同的N行N列的数字矩阵。第(i+1)行第j个数字描述了i和j之间的比赛结果,1表示i赢了j,0表示i负于j,与输入矩阵不同的是,在这个矩阵中没有表示比赛尚未进行的数字2;对角线上的数字都是0。输出矩阵要保证合法,不能发生矛盾。
输入样例#1:
3 0 1 2 0 0 2 2 2 0
输出样例#1:
1 0 1 0 0 0 1 1 0 0
【评分标准】
对于每个测试点,仅当你的程序的输出第一行的数字和标准答案一致,且给出了一个与之一致的合法方案,你才能得到该测试点的满分,否则该测试点得0分。
【数据范围】
30%的数据中,N≤6;
100%的数据中,N≤100。
考虑一下这样的三元组的相关性质,比如:1.这是个三元环,好像没用。2.三元组构成的子图中,所有点的入度/出度都是1,好像也没用。正难则反,我们考虑一下不符合条件的三元组,则子图中存在点的入度为2,也存在点的入度为0,出度也有类似性质。我们不妨考虑入度,假如点i的入度为d_i,则不合法的三元组个数是\sum_{i=1}^n \mathrm{C}_{d_i}^2,这是因为任意选择两个有出边连向i的点与i组成三元组都是不合法的,而且由于是有向图,这个统计并不会重复。现在我们有办法求出不合法的三元组个数了,用总三元组数减去它就是合法的三元组数了,即答案是
\mathrm{C}_n^3 - \sum_{i=1}^n \mathrm{C}_{d_i}^2
其中
\mathrm{C}_n^3 = \frac{n(n-1)(n-2)}{6}
我们考虑一条不确定的边对它所连接的两个点的入度造成的影响,以及对答案造成的影响。实际上一条不确定的边会导致它连接的两个点其中一个点的入度+1,而我们知道有
\mathrm{C}_n^2 - \mathrm{C}_{n-1}^2 = n-1
这就是一个费用递增的模型!我们可以建立源→不确定的边→原图中的点→汇的网络。其中源→不确定的边→原图中的点的所有边为容量1费用0的边,表示选择一种方案。而用原图中的点→汇的边来表示费用递增,即设置为容量1费用从确定的入度到入度上限的一系列边,每一条边表示入度+1对答案的贡献。在这个网络中跑最小费用最大流即可。
对于输出方案,我们检查不确定的边在网络中的对应点的出边,看流流向了哪边,就可以确定该边在方案中的方向。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005, INF = 1e9;
struct Edge {
int to, cap, cost, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int cap, int cost) {
gra[tot] = Edge {v, cap, cost, head[u]}; head[u] = tot++;
gra[tot] = Edge {u, 0, -cost, head[v]}; head[v] = tot++;
}
int f[MAXN], dis[MAXN], pre[MAXN], pree[MAXN];
std::queue<int> que;
bool inque[MAXN];
inline bool spfa(int s, int t) {
memset(f, 0, sizeof(f));
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; inque[s] = true; f[s] = INF; que.push(s);
while(!que.empty()) {
int u = que.front(); que.pop(); inque[u] = false;
for(int i = head[u]; ~i; i = gra[i].nxt) {
int v = gra[i].to;
if(gra[i].cap > 0 && dis[v] > dis[u] + gra[i].cost) {
pre[v] = u; pree[v] = i;
f[v] = std::min(f[u], gra[i].cap);
dis[v] = dis[u] + gra[i].cost;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
return f[t];
}
int flow, cost;
inline void mcmf(int s, int t) {
while(spfa(s, t)) {
for(int i = t; i != s; i = pre[i]) {
gra[pree[i]].cap -= f[t];
gra[pree[i] ^ 1].cap += f[t];
}
flow += f[t];
cost += f[t] * dis[t];
}
}
int n, m, mmp[105][105], deg[105], S, T;
// 1 ~ n point
// n+1 ~ edge
int main() {
memset(head, -1, sizeof(head));
m = n = readint();
S = n * n + 1; T = S + 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
mmp[i][j] = readint();
if(mmp[i][j] == 2 && i < j) {
addedge(S, ++m, 1, 0);
addedge(m, i, 1, 0);
addedge(m, j, 1, 0);
} else if(mmp[i][j] == 1) {
deg[j]++;
}
}
}
for(int i = 1; i <= n; i++) {
cost += deg[i] * (deg[i] - 1) / 2;
for(int j = deg[i]; j < n - 1; j++) {
addedge(i, T, 1, j);
}
}
mcmf(S, T);
printf("%d\n", n * (n - 1) * (n - 2) / 6 - cost);
m = n;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(mmp[i][j] == 2) {
int to;
for(int k = head[++m]; ~k; k = gra[k].nxt) {
if(gra[k].cap == 0) {
to = gra[k].to;
break;
}
}
if(to == j) {
mmp[i][j] = 1; mmp[j][i] = 0;
} else if(to == i) {
mmp[j][i] = 1; mmp[i][j] = 0;
}
}
printf("%d ", mmp[i][j]);
}
puts("");
}
return 0;
}
题目地址:洛谷:【P2046】[NOI2010]海拔 – 洛谷、BZOJ:Problem 2007. — [Noi2010]海拔
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域。简单起见,可以将YT市看作 一个正方形,每一个区域也可看作一个正方形。从而,YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路(简称道路),每条双向 道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2×2个区域,包括3×3个交叉路口和12条双向道路。
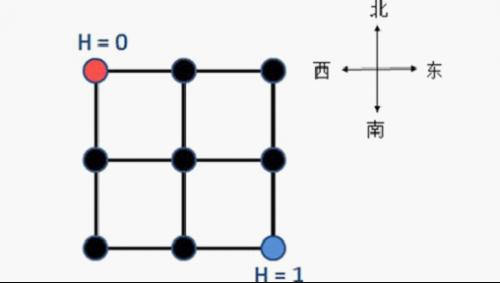
小Z作为该市的市长,他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量,即在高峰期间沿 着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗h的体力。如果 是下坡的话,则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数),那么一个人经过这段路所消耗的体力是max{0, h}(这里max{a, b}表示取a, b两个值中的较大值)。
小Z还测量得到这个城市西北角的交叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡消耗的总体力和的最小值。
输入格式:
第一行包含一个整数n,含义如上文所示。
接下来4n(n + 1)行,每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序:n(n + 1)个数表示所有从西到东方向的人流量,然后n(n + 1)个数表示所有从北到南方向的人流量,n(n + 1)个数表示所有从东到西方向的人流量,最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向,输入顺序按照起点由北向南,若南北方向相同时由西到东的顺序给出(参见样例输入)。
输出格式:
仅包含一个数,表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和(即总体力和的最小值),结果四舍五入到整数。
输入样例#1:
1 1 2 3 4 5 6 7 8
输出样例#1:
3
对于20%的数据:n ≤ 3;
对于50%的数据:n ≤ 15;
对于80%的数据:n ≤ 40;
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
我们发现这些方格在最优解上的高度肯定非0即1,且有一条明显的分界线。因此我们只需要找出一些跨越分界线的边,计算它们的贡献即可。这实际上可以看成一个最小割。
既然我们把原问题转化成了最小割问题,就可以继续转化为对偶图上的最短路问题。由于是方格图,对偶图很好建立。
需要注意的是双向边问题,我们只需要在对偶图上也建立方向相反权值不同的有向边即可。例如我们将向下向右的边建为S→T方向,则向上向左的边要建为T→S方向,随后跑一遍最短路即可。通过验证,S、T的选择与边的方向选择的两种方案是等价的,因此可以任意选择S和T的位置。下面的代码中,上边界和右边界与T相连,下边界和左边界与S相连。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>
#include <queue>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 1000005;
struct Edge {
int to, w, nxt;
} gra[MAXN << 1];
int head[MAXN], tot;
inline void addedge(int u, int v, int w) {
gra[tot] = Edge {v, w, head[u]}; head[u] = tot++;
}
int dis[MAXN];
bool inque[MAXN];
struct Queue {
int l, r, q[MAXN];
inline void clear() {
l = r = 0;
}
Queue() {
clear();
}
inline int front() {
return q[l];
}
inline void push(int x) {
q[r++] = x;
if(r >= MAXN) r -= MAXN;
}
inline void pop() {
l++;
if(l >= MAXN) l -= MAXN;
}
inline bool empty() {
return l == r;
}
} que;
inline void spfa(int s) {
que.clear();
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; inque[s] = true;
que.push(s);
while(!que.empty()) {
register int u = que.front(); que.pop(); inque[u] = false;
for(int i = head[u]; ~i; i = gra[i].nxt) {
register int v = gra[i].to;
if(dis[v] > dis[u] + gra[i].w) {
dis[v] = dis[u] + gra[i].w;
if(!inque[v]) {
inque[v] = true;
que.push(v);
}
}
}
}
}
int n, t, S, T;
int main() {
memset(head, -1, sizeof(head));
n = readint();
S = 0; T = n * n + 1;
for(register int i = 1; i <= n + 1; i++) {
for(register int j = 1; j <= n; j++) {
t = readint();
if(i == 1) {
addedge((i - 1) * n + j, T, t);
} else if(i == n + 1) {
addedge(S, (i - 2) * n + j, t);
} else {
addedge((i - 1) * n + j, (i - 2) * n + j, t);
}
}
}
for(register int i = 1; i <= n; i++) {
for(register int j = 1; j <= n + 1; j++) {
t = readint();
if(j == 1) {
addedge(S, (i - 1) * n + j, t);
} else if(j == n + 1) {
addedge((i - 1) * n + j - 1, T, t);
} else {
addedge((i - 1) * n + j - 1, (i - 1) * n + j, t);
}
}
}
for(register int i = 1; i <= n + 1; i++) {
for(register int j = 1; j <= n; j++) {
t = readint();
if(i == 1) {
addedge(T, (i - 1) * n + j, t);
} else if(i == n + 1) {
addedge((i - 2) * n + j, S, t);
} else {
addedge((i - 2) * n + j, (i - 1) * n + j, t);
}
}
}
for(register int i = 1; i <= n; i++) {
for(register int j = 1; j <= n + 1; j++) {
t = readint();
if(j == 1) {
addedge((i - 1) * n + j, S, t);
} else if(j == n + 1) {
addedge(T, (i - 1) * n + j - 1, t);
} else {
addedge((i - 1) * n + j, (i - 1) * n + j - 1, t);
}
}
}
spfa(S);
printf("%d", dis[T]);
return 0;
}