比赛地址：Dashboard – Codeforces Round #462 (Div. 2) – Codeforces，也可以在底下的赛题列表点进题目。

赛题列表

#A 934A – A Compatible Pair | 暴力，枚举
#B 934B – A Prosperous Lot | 贪心
#C 933A – A Twisty Movement | 枚举
#D 933B – A Determined Cleanup | 数学
#E 933C – A Colourful Prospect | 计算几何

934A A Compatible Pair

题目描述

给两个数列a, b长分别为n, m，其中a数列要删去一个数，求一种删数的方案，使得所有a_i \cdot b_j中的最大值最小。只需要输出这个最小值。
数据范围：2 \leq n, m \leq 50

样例

样例1

输入：

2 2
20 18
2 14

输出：

252

说明：
删去20，此时最大值为18*14=252。

样例2

输入：

5 3
-1 0 1 2 3
-1 0 1

输出：

2

说明：
删去3，最大值为2*1=2。

题解

枚举删去的数，然后枚举求出此时最大值，维护全部情况的最大值的最小值即可。
复杂度：O(n^3)

代码

// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>

int n, m;
long long ans = 1e18 + 10;
long long a[55], b[55];

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    for(int i = 1; i <= m; i++) {
        scanf("%lld", &b[i]);
    }
    for(int k = 1; k <= n; k++) {
        long long mx = -1e18 - 10;
        for(int i = 1; i <= n; i++) {
            if(i == k) continue;
            for(int j = 1; j <= m; j++) {
                mx = std::max(mx, a[i] * b[j]);
            }
        }
        ans = std::min(ans, mx);
    }
    printf("%lld", ans);
    return 0;
}

934B A Prosperous Lot

题目描述

定义一个数的圈的个数为这个数中包含数码的圈的个数和，其中，数码的圈的个数依照下图计算。

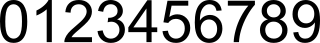
例如，8的圈的个数为2，而5的圈的个数为0。
给定一个数k，求任意一个不大于10^{18}的非负整数使得其圈的个数为k。如果不存在，输出-1。
数据范围：1 \leq k \leq 10^6

样例

样例1

输入：

2

输出：

462

样例2

输入：

6

输出：

8080

题解

我们知道8有两个圈，而6有一个圈。先贪心一下，全用8，如果还剩下1就用1个6，加一起长度超没超18。超了就无解，没超就输出。
复杂度：O(1)

代码

// Code by KSkun, 2018/2
#include <cstdio>

int k, c2, c1;

int main() {
    scanf("%d", &k);
    c2 = k / 2;
    c1 = k % 2;
    if(c1 + c2 > 18) {
        printf("-1");
        return 0;
    } 
    if(c1) putchar('6');
    for(int i = 1; i <= c2; i++) putchar('8');
    return 0;
}

933A A Twisty Movement

题目描述

给定一个只由1和2构成的数列，长为n，有一次机会翻转任意区间[l, r]，求一种翻转方法，使得翻转后的序列的LIS最长。只需要输出最长的LIS长度。
数据范围：1 \leq n \leq 2000

样例

样例1

输入：

4
1 2 1 2

输出：

4

说明：
翻转区间[2, 3]得到序列1 1 2 2。

样例2

输入：

10
1 1 2 2 2 1 1 2 2 1

输出：

9

说明：翻转区间[3, 7]得到序列1 1 1 1 2 2 2 2 2 1。

题解

这个题需要一些思考。
首先传统的LIS求法是O(n \log n)的，但是12序列可以做到O(n)的。枚举LIS中1和2的分界点，即为该点前1的个数加该点后2的个数。可以分别预处理出来。
我们考虑枚举分界点，然后枚举翻转的区间。可以发现，如果分界点不在区间内部，翻转区间是没有用的。所以区间应该包含这个分界点。翻转后的答案应该是1~区间左端点1的个数+区间左端点~分界点2的个数+分界点~区间右端点1的个数+区间右端点~n 2的个数。左端点和右端点的计算是分开的，所以可以分开枚举分别求最大值，加起来就是一个完整的最大值。
复杂度：O(n^2)

代码

// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>

int n, a[2005], c1[2005], c2[2005], ans = 0;

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        c1[i] = c1[i - 1];
        c2[i] = c2[i - 1];
        if(a[i] == 1) {
            c1[i]++;
        } else {
            c2[i]++;
        }
    }
    for(int i = 0; i <= n; i++) {
        ans = std::max(ans, c1[i] + c2[n] - c2[i]);
    }
    for(int i = 0; i <= n; i++) {
        int mx1 = 0, mx2 = 0;
        for(int l = 1; l < i; l++) {
            mx1 = std::max(mx1, c1[l - 1] + c2[i - 1] - c2[l - 1]);
        }
        for(int r = i; r <= n; r++) {
            mx2 = std::max(mx2, c1[r] - c1[i - 1] + c2[n] - c2[r]);
        }
        ans = std::max(ans, mx1 + mx2);
    }
    printf("%d", ans);
    return 0;
}

933B A Determined Cleanup

题目描述

给两个数p和k，要求求一个多项式f(x)，使得f(x)满足f(x)=q(x) \cdot (x+k)+p，其中q(x)是另一个多项式，且f(x)各项的系数和常数项都不大于k。如果无解，输出-1。
数据范围：1 \leq p \leq 10^{18}, 2 \leq k \leq 2000

样例

样例1

输入：

46 2

输出：

7
0 1 0 0 1 1 1

说明：
f(x) = x^6 + x^5 + x^4 + x = (x^5 - x^4 + 3x^3 - 6x^2 + 12x - 23)(x + 2) + 46

样例2

输入：

2018 214

输出：

3
92 205 1

说明：
f(x) = x^2 + 205x + 92 = (x - 9)(x + 214) + 2018

题解

本题需要用到余式定理。余式定理的内容是多项式f(x)除以多项式(x – a)的余式为f(a)。
余式定理的证明可以参考余式定理_百度百科。
这里需要f(x)除以(x + k)余p，就是说f(-k) = p。那么我们只需要将p化成一个-k进制数即可。这样看来，本题不存在无解的情况。
复杂度：O(\log p)

代码

// Code by KSkun, 2018/2
#include <cstdio>
#include <vector>

long long p;
int k;

std::vector<int> vec;

int main() {
    scanf("%lld%d", &p, &k);
    while(p != 0) {
        vec.push_back((p % k + k) % k);
        p = (vec.back() - p) / k;
    }
    printf("%d\n", vec.size());
    for(int i = 0; i < vec.size(); i++) {
        printf("%d ", vec[i]);
    } 
    return 0;
} 

933C A Colourful Prospect

题目描述

给n个圆，求n个圆将平面分成几个区域（内部不包含任何弧线）。
数据范围：1 \leq n \leq 3

样例

样例1

输入：

3
0 0 1
2 0 1
4 0 1

输出：

4

说明：

样例2

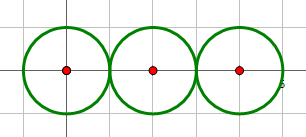
输入：

3
0 0 2
3 0 2
6 0 2

输出：

6

说明：

样例3

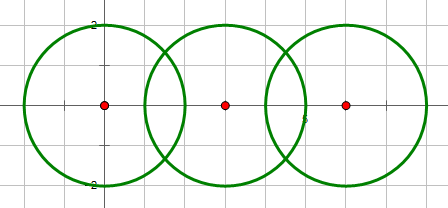
输入：

3
0 0 2
2 0 2
1 1 2

输出：

8

说明：

题解

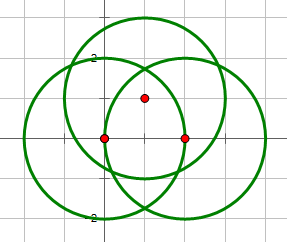
需要使用欧拉定理（V-E+F=2）解决。暂未解决。
复杂度：