概述

树链剖分是一种将树上的链划分为轻重链，从而实现降低复杂度的处理方式。剖分后的树，单次查询LCA的复杂度为O(\log n)，与Tarjan-LCA算法与倍增算法复杂度相同，但是树剖可以在线，非常好用。

原理与实现

轻重链

我们把一个有根树一个点子树最大的儿子叫做这个点的重儿子，重儿子连接成的链为重链，而其他的链叫做轻链。每个点都有重儿子，因此重链可能并不连续。但是，可以证明一个点到根的路径上的链数为O(\log n)级别的。
下面是一棵剖分好了的树，图片来自[知识点]树链剖分 – jinkun113 – 博客园，感谢原作者。

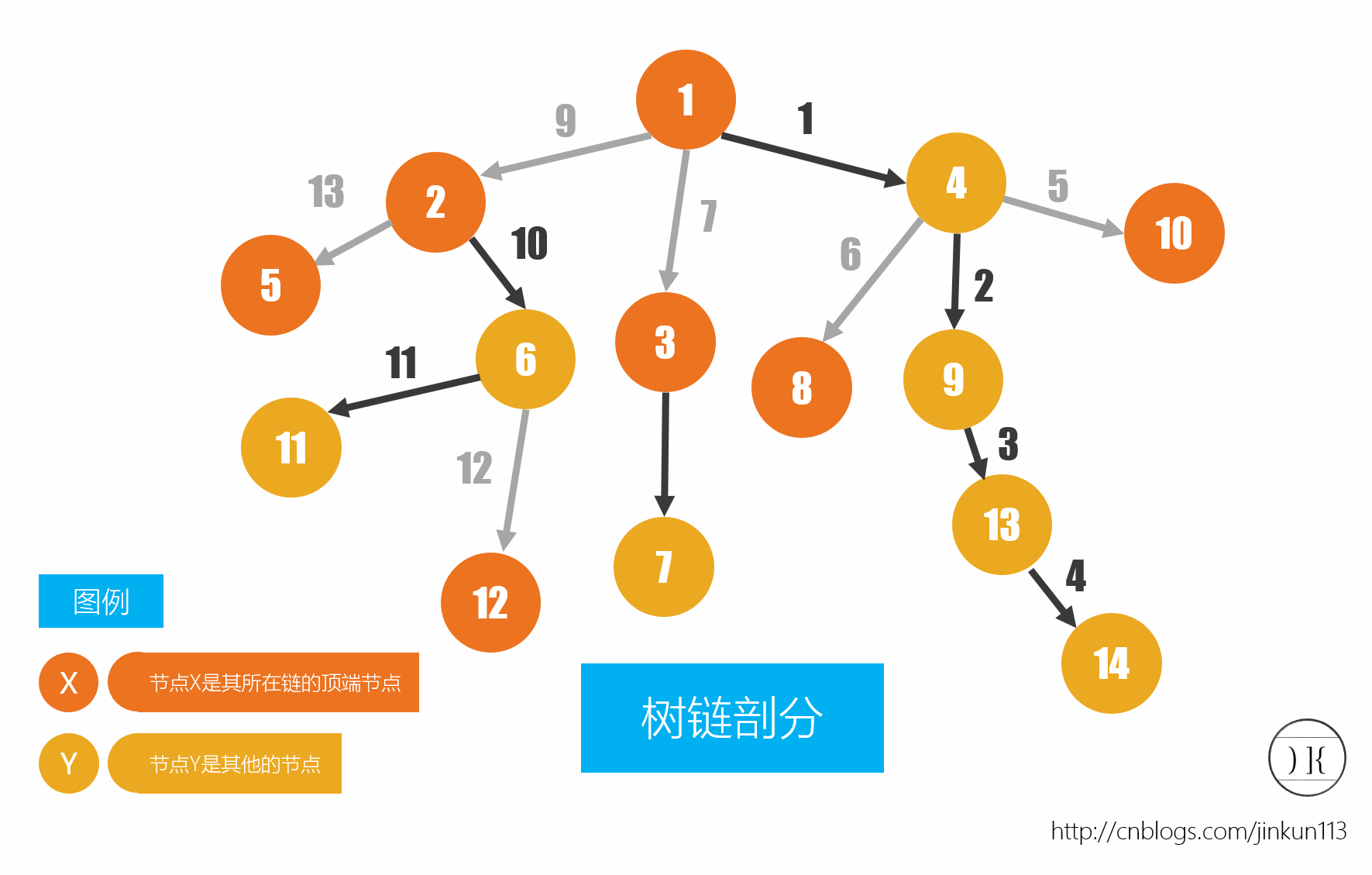
如果我们每次从查询LCA的两个点上跳到他们所在的链顶，直到他们的链顶相同，就能够完成查询LCA的工作。
下面是树剖的两个DFS，用于处理子树信息与划分轻重链。

// 处理子树信息
void dfs1(int u) {
    int mx = -1;
    for(int i = head[u]; i != -1; i = gra[i].nxt) {
        int v = gra[i].to;
        if(v == fa[u]) continue;
        dep[v] = dep[u] + 1;
        fa[v] = u;
        siz[u]++;
        dfs1(v);
        siz[u] += siz[v];
        if(siz[v] > mx) {
            mx = siz[v];
            son[u] = v;
        }
    } 
}

// 处理链信息
void dfs2(int u, int tp) {
    top[u] = tp;
    if(son[u] != 0) {
        // 优先遍历重儿子
        dfs2(son[u], tp);
    }
    for(int i = head[u]; i != -1; i = gra[i].nxt) {
        int v = gra[i].to;
        if(v == son[u] || v == fa[u]) continue;
        dfs2(v, v);
    }
}

查询LCA可以使用下面的实现。

int findlca(int u, int v) {
    int f1 = top[u], f2 = top[v];
    while(f1 != f2) {
        if(dep[f1] > dep[f2]) {
            std::swap(f1, f2);
            std::swap(u, v);
        }
        v = fa[f2];
        f2 = top[v];
    }
    if(dep[u] < dep[v]) return u; else return v;
}

DFS序

虽然划分了轻重链，但是只有这些信息我们也只能找个LCA。如果想维护链上信息，我们可以使用DFS序。在dfs2的时候把前序遍历的DFS序处理出来，连续的一段代表一个子树，而由于优先遍历重链，重链也是连续的一段。这样，我们就可以想办法套数据结构来统计链上信息了。
下面是统计DFS序版本的dfs2。

void dfs2(int u, int tp) {
    top[u] = tp;
    pos[u] = stn++;
    if(son[u] != -1) {
        dfs2(son[u], tp);
    }
    for(int e = head[u]; e != -1; e = gra[e].nxt) {
        int v = gra[e].to;
        if(v == son[u] || v == fa[u]) continue;
        dfs2(v, v);
    }
}

例题1：【P3379】【模板】最近公共祖先（LCA） – 洛谷

LCA在线查询，树剖疾如岛风哦~

// Code by KSkun, 2017/11
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm> 

struct io {
    char buf[1 << 26], *s;

    io() {
        fread(s = buf, 1, 1 << 26, stdin);
    }

    inline int read() {
        register int res = 0;
        while(*s < '0' || *s > '9') s++;
        while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
        return res;
    }
} ip;

#define read ip.read

int n, m, s, x, y, a, b;

struct Edge {
    int to, nxt;
} gra[1000005];
int head[500005], tot = 0;

inline void aedge(int u, int v) {
    gra[tot].nxt = head[u];
    gra[tot].to = v;
    head[u] = tot++;
}

int dep[500005], siz[500005], son[500005], fa[500005], top[500005];

void dfs1(int u) {
    int mx = -1;
    for(int i = head[u]; i != -1; i = gra[i].nxt) {
        int v = gra[i].to;
        if(v == fa[u]) continue;
        dep[v] = dep[u] + 1;
        fa[v] = u;
        siz[u]++;
        dfs1(v);
        siz[u] += siz[v];
        if(siz[v] > mx) {
            mx = siz[v];
            son[u] = v;
        }
    } 
}

void dfs2(int u, int tp) {
    top[u] = tp;
    if(son[u] != 0) {
        dfs2(son[u], tp);
    }
    for(int i = head[u]; i != -1; i = gra[i].nxt) {
        int v = gra[i].to;
        if(v == son[u] || v == fa[u]) continue;
        dfs2(v, v);
    }
}

int findlca(int u, int v) {
    int f1 = top[u], f2 = top[v];
    while(f1 != f2) {
        if(dep[f1] > dep[f2]) {
            std::swap(f1, f2);
            std::swap(u, v);
        }
        v = fa[f2];
        f2 = top[v];
    }
    if(dep[u] < dep[v]) return u; else return v;
}

int main() {
    memset(head, -1, sizeof head);
    n = read(); m = read(); s = read();
    for(int i = 0; i < n - 1; i++) {
        x = read(); y = read();
        aedge(x, y);
        aedge(y, x);
    }
    dfs1(s);
    dfs2(s, s);
    for(int i = 0; i < m; i++) {
        a = read(); b = read();
        printf("%d\n", findlca(a, b));
    }
    return 0;
}

例题2：【P3384】【模板】树链剖分 – 洛谷

线段树维护链信息和子树信息w

// Code by KSkun, 2017/10
#include <cstdio>
#include <cctype> 
#include <cstring>
typedef long long LL;

inline int read() {
    register int res = 0;
    register bool neg = false;
    char c = '*';
    while(!isdigit(c)) {
        if(c == '-') neg = true;
        c = getchar();
    }
    while(isdigit(c)) res *= 10, res += c - '0', c = getchar();
    if(neg) res *= -1;
    return res;
}

int n, m, r, p;

// Seg Tree
#define lch o << 1
#define rch (o << 1) | 1
#define mid ((l + r) >> 1)

LL a[100005], tree[400005], lazy[400005];

inline void build(int o, int l, int r) {
    if(l == r) {
        tree[o] = a[l];
        return;
    }
    build(lch, l, mid);
    build(rch, mid + 1, r);
    tree[o] = tree[lch] + tree[rch];
}

inline void pushdown(int o, int l, int r) {
    if(lazy[o] != 0) {
        lazy[lch] += lazy[o];
        lazy[rch] += lazy[o];
        tree[lch] += lazy[o] * (mid - l + 1);
        tree[rch] += lazy[o] * (r - mid);
        lazy[o] = 0;
    }
}

inline void add(int o, int l, int r, int ll, int rr, int v) {
    if(l >= ll && r <= rr) {
        tree[o] += v * (r - l + 1);
        lazy[o] += v;
        return;
    }
    pushdown(o, l, r);
    if(ll <= mid) add(lch, l, mid, ll, rr, v);
    if(rr > mid) add(rch, mid + 1, r, ll, rr, v);
    tree[o] = tree[lch] + tree[rch];
}

inline LL query(int o, int l, int r, int ll, int rr) {
    if(l >= ll && r <= rr) { 
        return tree[o];
    } 
    pushdown(o, l, r);
    LL sum = 0;
    if(ll <= mid) sum += query(lch, l, mid, ll, rr);
    if(rr > mid) sum += query(rch, mid + 1, r, ll, rr);
    return sum;
} 

// Poufen

struct Edge {
    int to, nxt;
} gra[200005];
int head[100005], tot = 0;

inline void addedge(int u, int v) {
    gra[tot].to = v;
    gra[tot].nxt = head[u];
    head[u] = tot++;
}

int dep[100005], siz[100005], son[100005], pos[100005], 
    fa[100005], top[100005], val[100005], stn = 1;

void dfs1(int u) {
    int e = head[u], mx = -1;
    while(e != -1) {
        int v = gra[e].to;
        if(v == fa[u]) {
            e = gra[e].nxt;
            continue;
        }
        dep[v] = dep[u] + 1;
        fa[v] = u;
        siz[u]++;
        dfs1(v);
        siz[u] += siz[v];
        if(siz[v] > mx) {
            son[u] = v;
            mx = siz[v];
        }
        e = gra[e].nxt;
    } 
}

void dfs2(int u, int tp) {
    top[u] = tp;
    pos[u] = stn++;
    if(son[u] != -1) {
        dfs2(son[u], tp);
    }
    int e = head[u];
    while(e != -1) {
        int v = gra[e].to;
        if(v == son[u] || v == fa[u]) {
            e = gra[e].nxt;
            continue;
        }
        dfs2(v, v);
        e = gra[e].nxt;
    }
}

inline void addpath(int x, int y, int val) {
    int fx = top[x], fy = top[y];
    while(fx != fy) {
        if(dep[fx] >= dep[fy]) {
            add(1, 1, n, pos[fx], pos[x], val);
            x = fa[fx];
        } else {
            add(1, 1, n, pos[fy], pos[y], val);
            y = fa[fy];
        }
        fx = top[x], fy = top[y];
    }
    if(pos[x] <= pos[y] || x == y) {
        add(1, 1, n, pos[x], pos[y], val);
    } else {
        add(1, 1, n, pos[y], pos[x], val);
    }
}

inline LL querypath(int x, int y) {
    LL res = 0;
    int fx = top[x], fy = top[y];
    while(fx != fy) {
        if(dep[fx] >= dep[fy]) {
            res += query(1, 1, n, pos[fx], pos[x]);
            x = fa[fx];
        } else {
            res += query(1, 1, n, pos[fy], pos[y]);
            y = fa[fy];
        }
        fx = top[x], fy = top[y];
    }
    if(pos[x] <= pos[y] || x == y) {
        res += query(1, 1, n, pos[x], pos[y]);
    } else {
        res += query(1, 1, n, pos[y], pos[x]);
    }
    return res;
}

inline void addsubt(int x, int v) {
    add(1, 1, n, pos[x], pos[x] + siz[x], v);
}

inline LL querysubt(int x) {
    return query(1, 1, n, pos[x], pos[x] + siz[x]);
}

int op, x, y, z;

int main() {
    n = read(), m = read(), r = read(), p = read();
    memset(head, -1, sizeof head);
    memset(son, -1, sizeof son);
    memset(fa, -1, sizeof fa);
    for(int i = 1; i <= n; i++) {
        val[i] = read();
    }
    for(int i = 0; i < n - 1; i++) {
        x = read(), y = read();
        addedge(x, y);
        addedge(y, x);
    }
    dep[r] = 0;
    fa[r] = r;
    dfs1(r);
    top[r] = r;
    dfs2(r, r);
    for(int i = 1; i <= n; i++) {
        a[pos[i]] = val[i];
    }
    build(1, 1, n);
    for(int i = 0; i < m; i++) {
        op = read();
        if(op == 1) {
            x = read(), y = read(), z = read();
            addpath(x, y, z);
        } else if(op == 2) {
            x = read(), y = read();
            printf("%lld\n", querypath(x, y) % p);
        } else if(op == 3) {
            x = read(), z = read();
            addsubt(x, z);
        } else if(op == 4) {
            x = read();
            printf("%lld\n", querysubt(x) % p);
        }
    }
    return 0;
}