注：本文部分图片来自互联网，其相关权利归原作者所有，感谢原作者的分享。

概述

Trie树是一种具有字符串插入和查找功能的数据结构，又称前缀树。这里介绍它的原理和实现。

原理

结构

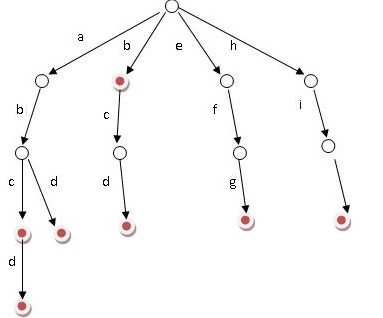
如上图，这就是一棵Trie树。这个Trie树中包含的单词有abc、abd、abcd、b、bcd、efg和hij。可以看到，Trie的字母并不存在结点上，而是存在边上。每个结点的儿子表示以这个结点对应的前缀的字符串的延续。结点的标记代表字符串的终止。这就是一棵Trie树的结构。

查找

了解了它的结构特征后，我们尝试查找一个给定字符串。这一步骤的核心操作就是下跳。从根节点开始，逐字符下跳，直到没有对应的字符或者终止节点无标记，代表查找失败。而如果一直有对应的字符且终止节点有标记代表查找成功。如果能跳出一段，代表当前Trie树中有字符串与查找串有公共前缀。
各位可以在上图中自己尝试一下。

插入

同样是下跳，区别是在找不到字符时候手动建新结点，再给终止结点打标记。各位可以在上图手动尝试插入。

示例

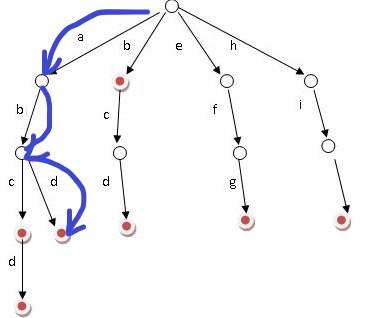
查找abd成功。

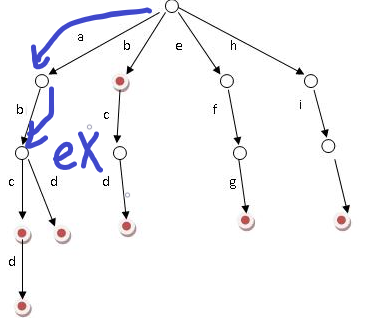
查找abe失败。

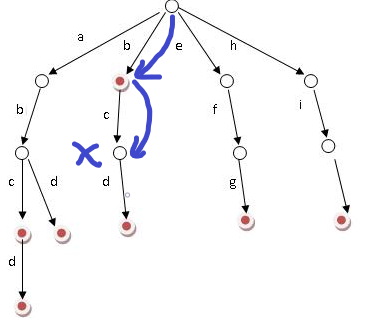
查找bc失败。

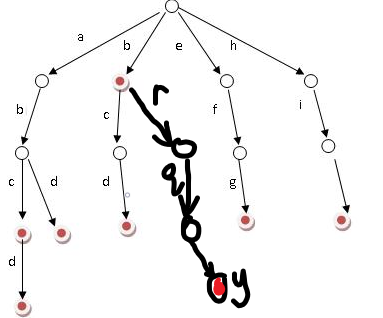
插入brqy。

实现

准备工作

用一个结构体Node来存储结点信息。

struct Node {
    bool wrd;
    int ch[26];
}

其中wrd表示结点是否是字符串的结尾，ch表示不同字符边对应的儿子编号。
创建Node数组表示整个Trie树，并以Node[1]作为树根。用siz变量统计目前结点数。

查找

inline bool search(char* str) {
    int t = 1;
    for(int i = 0; i < strlen(str); i++) {
        if(!trie[t].ch[str[i] - 'a']) {
            return false;
        } else {
            t = trie[t].ch[str[i] - 'a'];
        }
    }
    if(trie[t].wrd) {
        return true;
    } else {
        return false;
    }
}

模拟下跳过程，检查是否有结点、是否有标记。

插入

inline void insert(char* str) {
    int t = 1;
    for(int i = 0; i < strlen(str); i++) {
        if(!trie[t].ch[str[i] - 'a']) {
            t = trie[t].ch[str[i] - 'a'] = ++siz;
        } else {
            t = trie[t].ch[str[i] - 'a'];
        }
    }
    trie[t].wrd = true;
}

动态开节点，加标记。

一道例题：于是他错误的点名开始了

题意

插入字符串，查找字符串，判断字符串找没找过。

题解

Trie可以胜任前两个操作。至于判断是否找过，在结束结点上记录访问过没有即可。

代码

// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>

struct Node {
    bool wrd, vis;
    int ch[26];
} trie[500005];
int siz = 1;

inline void insert(char* str) {
    int t = 1;
    for(int i = 0; i < strlen(str); i++) {
        if(!trie[t].ch[str[i] - 'a']) {
            t = trie[t].ch[str[i] - 'a'] = ++siz;
        } else {
            t = trie[t].ch[str[i] - 'a'];
        }
    }
    trie[t].wrd = true;
}

inline int search(char* str) {
    int t = 1;
    for(int i = 0; i < strlen(str); i++) {
        if(!trie[t].ch[str[i] - 'a']) {
            return 0;
        } else {
            t = trie[t].ch[str[i] - 'a'];
        }
    }
    if(trie[t].wrd) {
        if(trie[t].vis) return -1;
        trie[t].vis = true;
        return 1;
    } else {
        return 0;
    }
}

int n, m;
char str[55];

int main() {
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        scanf("%s", str);
        insert(str);
    }
    scanf("%d", &m);
    for(int i = 0; i < m; i++) {
        scanf("%s", str);
        int res = search(str);
        if(res == 1) printf("OK\n");
        else if(res == -1) printf("REPEAT\n");
        else printf("WRONG\n");
    }
    return 0;
}