Codeforces Round #462 (Div. 2) 题解
比赛地址:Dashboard – Codeforces Round #462 …
May all the beauty be blessed.
题目地址:洛谷:【P3273】[SCOI2011]棘手的操作 – 洛谷、BZOJ:Problem 2333. — [SCOI2011]棘手的操作
有N个节点,标号从1到N,这N个节点一开始相互不连通。第i个节点的初始权值为a[i],接下来有如下一些操作:
U x y: 加一条边,连接第x个节点和第y个节点A1 x v: 将第x个节点的权值增加vA2 x v: 将第x个节点所在的连通块的所有节点的权值都增加vA3 v: 将所有节点的权值都增加vF1 x: 输出第x个节点当前的权值F2 x: 输出第x个节点所在的连通块中,权值最大的节点的权值F3: 输出所有节点中,权值最大的节点的权值输入格式:
输入的第一行是一个整数N,代表节点个数。接下来一行输入N个整数,a[1], a[2], …, a[N],代表N个节点的初始权值。再下一行输入一个整数Q,代表接下来的操作数。最后输入Q行,每行的格式如题目描述所示。
输出格式:
对于操作F1, F2, F3,输出对应的结果,每个结果占一行。
输入样例#1:
3 0 0 0 8 A1 3 -20 A1 2 20 U 1 3 A2 1 10 F1 3 F2 3 A3 -10 F3
输出样例#1:
-10 10 10
对于30%的数据,保证 N<=100,Q<=10000
对于80%的数据,保证 N<=100000,Q<=100000
对于100%的数据,保证 N<=300000,Q<=300000
对于所有的数据,保证输入合法,并且 -1000<=v, a[1], a[2], …, a[N]<=1000
考虑离线解决这个题,我们可以把操作中同一连通块的元素连续地排列在一个序列中,这样连通块操作就变成了区间操作,这个可以用线段树维护区间最大值。
至于如何连续排列,可以考虑用链表来存储当前连通块序列,然后合并连通块的时候合并链表,这样就自然成为连续的一段了。最后再遍历链表给节点加编号就好。
使用可并堆做这个题目就很裸了,也不需要离线。这里我写的是左偏树。
分开管理两类可并堆,一类是联通块的大根堆,一类是所有联通块堆顶元素的大根堆(换句话说,这是一个维护全局的堆)。
U操作:将两个节点所在的堆合并,删去全局堆中消失的那个堆的对顶。
A1操作:将x所在堆中x元素删去,更新x元素的值,再插回去。
A2操作:将x所在堆全局增量加上v。堆全局增量可以在堆顶维护,需要统计这个结点的真实值的时候从该点一路上跳,跳到一个父亲就将该父亲的增量加入真实值。(因为堆并过程中增量仍然在被合并的堆顶)
A3操作:维护总全局增量加v。
F1操作:查询x的真实值。
F2操作:查询x所在堆堆顶的真实值。
F3操作:查询全局堆堆顶的真实值。
这个解法的代码我借鉴了远航之曲的实现思路。
// Code by KSkun, 2018/2
#include <cstdio>
#include <algorithm>
struct io {
char buf[1 << 26], *op;
io() {
fread(op = buf, 1, 1 << 26, stdin);
}
inline int readint() {
register int res = 0, neg = 1;
while(*op < '0' || *op > '9') if(*op++ == '-') neg = -1;
while(*op >= '0' && *op <= '9') res = res * 10 + *op++ - '0';
return res * neg;
}
inline char readchar() {
return *op++;
}
} ip;
#define readint ip.readint
#define readchar ip.readchar
inline bool isop(char c) {
return c == 'A' || c == 'U' || c == 'F';
}
inline char readop() {
char c;
while(!isop(c = readchar()));
return c;
}
int n, a[300005], q, opop1[300005], opx[300005], opy[300005], idx[300005], inv[300005], tot = 1;
char opop[300005];
// Linked List
int pre[300005], nxt[300005], head[300005], tail[300005];
// Union-Find
int fa[300005];
inline int find(int x) {
int r = x;
while(fa[r] != r) r = fa[r];
while(fa[x] != x) {
int ofa = fa[x];
fa[x] = r;
x = ofa;
}
return r;
}
// Seg Tree
#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)
int tree[1200005], lazy[1200005];
inline void build(int o, int l, int r) {
if(l == r) {
tree[o] = a[inv[l]];
return;
}
build(lch, l, mid);
build(rch, mid + 1, r);
tree[o] = std::max(tree[lch], tree[rch]);
}
inline void pushdown(int o) {
if(lazy[o] != 0) {
lazy[lch] += lazy[o];
lazy[rch] += lazy[o];
tree[lch] += lazy[o];
tree[rch] += lazy[o];
lazy[o] = 0;
}
}
inline void add(int o, int l, int r, int ll, int rr, int v) {
if(l == ll && r == rr) {
tree[o] += v;
lazy[o] += v;
return;
}
pushdown(o);
if(rr <= mid) {
add(lch, l, mid, ll, rr, v);
} else if(ll > mid) {
add(rch, mid + 1, r, ll, rr, v);
} else {
add(lch, l, mid, ll, mid, v);
add(rch, mid + 1, r, mid + 1, rr, v);
}
tree[o] = std::max(tree[lch], tree[rch]);
}
inline int query(int o, int l, int r, int ll, int rr) {
if(l == ll && r == rr) {
return tree[o];
}
pushdown(o);
if(rr <= mid) {
return query(lch, l, mid, ll, rr);
} else if(ll > mid) {
return query(rch, mid + 1, r, ll, rr);
} else {
return std::max(query(lch, l, mid, ll, mid), query(rch, mid + 1, r, mid + 1, rr));
}
}
int main() {
n = readint();
for(int i = 1; i <= n; i++) {
a[i] = readint();
fa[i] = head[i] = tail[i] = i;
}
q = readint();
for(int i = 1; i <= q; i++) {
opop[i] = readop();
if(opop[i] == 'U') {
opx[i] = readint();
opy[i] = readint();
int f1 = find(opx[i]), f2 = find(opy[i]);
if(f1 != f2) {
fa[f2] = f1;
pre[head[f2]] = tail[f1];
nxt[tail[f1]] = head[f2];
tail[f1] = tail[f2];
}
} else if(opop[i] == 'A') {
opop1[i] = readint();
if(opop1[i] < 3) {
opx[i] = readint();
}
opy[i] = readint();
} else if(opop[i] == 'F') {
opop1[i] = readint();
if(opop1[i] < 3) {
opx[i] = readint();
}
}
}
for(int i = 1; i <= n; i++) {
if(!pre[i]) {
for(int j = i; j; j = nxt[j]) {
idx[j] = tot++;
inv[idx[j]] = j;
}
}
}
build(1, 1, n);
for(int i = 1; i <= n; i++) {
fa[i] = head[i] = tail[i] = i;
}
for(int i = 1; i <= q; i++) {
if(opop[i] == 'U') {
int f1 = find(idx[opx[i]]), f2 = find(idx[opy[i]]);
if(f1 != f2) {
fa[f2] = f1;
if(head[f1] < head[f2]) {
tail[f1] = tail[f2];
} else {
head[f1] = head[f2];
}
}
} else if(opop[i] == 'A') {
if(opop1[i] == 1) {
add(1, 1, n, idx[opx[i]], idx[opx[i]], opy[i]);
} else if(opop1[i] == 2) {
int f = find(idx[opx[i]]);
add(1, 1, n, head[f], tail[f], opy[i]);
} else {
add(1, 1, n, 1, n, opy[i]);
}
} else if(opop[i] == 'F') {
if(opop1[i] == 1) {
printf("%d\n", query(1, 1, n, idx[opx[i]], idx[opx[i]]));
} else if(opop1[i] == 2) {
int f = find(idx[opx[i]]);
printf("%d\n", query(1, 1, n, head[f], tail[f]));
} else {
printf("%d\n", query(1, 1, n, 1, n));
}
}
}
return 0;
}
// Code by KSkun, 2018/2
#include <cstdio>
#include <queue>
struct io {
char buf[1 << 26], *op;
io() {
fread(op = buf, 1, 1 << 26, stdin);
}
inline int readint() {
register int res = 0, neg = 1;
while(*op < '0' || *op > '9') if(*op++ == '-') neg = -1;
while(*op >= '0' && *op <= '9') res = res * 10 + *op++ - '0';
return res * neg;
}
inline char readchar() {
return *op++;
}
} ip;
#define readint ip.readint
#define readchar ip.readchar
inline bool isop(char c) {
return c == 'U' || c == 'A' || c == 'F';
}
inline void readop(char* str) {
char c;
while(!isop(c = readchar()));
str[0] = c;
if(c == 'A' || c == 'F') str[1] = readchar();
}
int n, m, x, y, z, add = 0;
char op[5];
struct LeftistTree {
int dis[300005], fa[300005], ch[300005][2], val[300005], add[300005], root;
inline int toadd(int x) {
int res = 0;
while(x = fa[x]) res += add[x];
return res;
}
inline void clear(int x) {
fa[x] = ch[x][0] = ch[x][1] = 0;
}
inline void pushdown(int x) {
if(ch[x][0]) {
val[ch[x][0]] += add[x];
add[ch[x][0]] += add[x];
}
if(ch[x][1]) {
val[ch[x][1]] += add[x];
add[ch[x][1]] += add[x];
}
add[x] = 0;
}
inline int merge(int x, int y) {
if(!x) return y;
if(!y) return x;
if(val[x] < val[y]) std::swap(x, y);
pushdown(x);
ch[x][1] = merge(ch[x][1], y);
fa[ch[x][1]] = x;
if(dis[ch[x][0]] < dis[ch[x][1]]) std::swap(ch[x][0], ch[x][1]);
dis[x] = dis[ch[x][1]] + 1;
return x;
}
inline int froot(int x) {
while(fa[x]) x = fa[x];
return x;
}
inline void delet(int x) {
pushdown(x);
int f = merge(ch[x][0], ch[x][1]);
fa[f] = fa[x];
if(fa[x]) ch[fa[x]][ch[fa[x]][0] == x ? 0 : 1] = f;
int t = fa[x];
if(!t) {
root = f;
return;
}
while(t) {
if(dis[ch[t][0]] < dis[ch[t][1]]) std::swap(ch[t][0], ch[t][1]);
if(dis[t] == dis[ch[t][1]] + 1) return;
dis[t] = dis[ch[t][1]] + 1;
if(!fa[t]) root = t;
t = fa[t];
}
}
inline void addtree(int x, int v) {
int rt = froot(x);
val[rt] += v;
add[rt] += v;
}
inline int addpoint(int x, int v) {
int rt = froot(x);
if(rt == x) {
if(!ch[x][0] && !ch[x][1]) {
val[x] += v;
return x;
} else {
rt = ch[x][0] ? ch[x][0] : ch[x][1];
}
}
delet(x);
val[x] += v + toadd(x);
clear(x);
return merge(froot(rt), x);
}
inline void build() {
std::queue<int> que;
for(int i = 1; i <= n; i++) {
que.push(i);
}
while(que.size() > 1) {
int x = que.front();
que.pop();
int y = que.front();
que.pop();
que.push(merge(x, y));
}
root = que.front();
}
};
LeftistTree lt1, lt2;
int main() {
n = readint();
for(int i = 1; i <= n; i++) {
lt1.val[i] = lt2.val[i] = readint();
}
lt1.dis[0] = lt2.dis[0] = -1;
lt2.build();
m = readint();
for(int i = 1; i <= m; i++) {
readop(op);
if(op[0] == 'U') {
x = readint();
y = readint();
int fx = lt1.froot(x), fy = lt1.froot(y), rt;
if(fx != fy) {
rt = lt1.merge(fx, fy);
if(rt == fx) lt2.delet(fy);
if(rt == fy) lt2.delet(fx);
}
}
if(op[0] == 'A') {
if(op[1] == '1') {
x = readint();
y = readint();
int fx = lt1.froot(x), rt;
lt2.delet(fx);
rt = lt1.addpoint(x, y);
lt2.val[rt] = lt1.val[rt];
lt2.clear(rt);
lt2.root = lt2.merge(lt2.root, rt);
}
if(op[1] == '2') {
x = readint();
y = readint();
int fx = lt1.froot(x);
lt2.delet(fx);
lt1.val[fx] += y;
lt1.add[fx] += y;
lt2.val[fx] = lt1.val[fx];
lt2.clear(fx);
lt2.root = lt2.merge(lt2.root, fx);
}
if(op[1] == '3') {
x = readint();
add += x;
}
}
if(op[0] == 'F') {
if(op[1] == '1') {
x = readint();
printf("%d\n", lt1.val[x] + lt1.toadd(x) + add);
}
if(op[1] == '2') {
x = readint();
printf("%d\n", lt1.val[lt1.froot(x)] + add);
}
if(op[1] == '3') {
printf("%d\n", lt2.val[lt2.root] + add);
}
}
}
return 0;
}
因为经常WA,手写了一个数据生成器,偶尔会崩掉不要介意qwq,可自由调整n和q的取值。
// Code by KSkun, 2018/2
#include <cstdio>
#include <cstdlib>
#include <ctime>
int n, q;
char str[10][5] = {"U", "A1", "A2", "A3", "F1", "F2", "F3"};
int main() {
freopen("p3273.in", "w", stdout);
srand(time(NULL));
n = rand() % 50;
q = rand() % 50;
printf("%d\n", n);
for(int i = 1; i <= n; i++) {
printf("%d ", rand() - RAND_MAX / 2);
}
printf("\n");
printf("%d\n", q);
for(int i = 1; i <= q; i++) {
int op = rand() % 7;
printf("%s ", str[op]);
if(op == 0) {
printf("%d %d ", rand() % n + 1, rand() % n + 1);
}
if(op == 1 || op == 2 || op == 4 || op == 5) {
printf("%d ", rand() % n + 1);
}
if(op == 1 || op == 2 || op == 3) {
printf("%d ", rand() - RAND_MAX / 2);
}
printf("\n");
}
return 0;
}
题目地址:POJ:1151 — Atlantis、vjudge:Atlantis – POJ 1151 – Virtual Judge
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
给若干矩形,求矩形并的总面积(即多个矩形重叠的部分只计算一次)。
输入格式:
The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.
The input file is terminated by a line containing a single 0. Don’t process it.
输出格式:
For each test case, your program should output one section. The first line of each section must be Test case #k, where k is the number of the test case (starting with 1). The second one must be Total explored area: a, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.
Output a blank line after each test case.
输入样例#1:
2 10 10 20 20 15 15 25 25.5 0
输出样例#1:
Test case #1 Total explored area: 180.00
本题是一个扫描线的经典应用,我们按x从小到大的顺序依次扫过矩形的每一条横边,统计每扫过这一段的覆盖宽度,计算出这一段的覆盖面积,加入答案。
具体而言,我们将y坐标离散化,这有利于用线段树存储y坐标。每扫到一个矩形的下边,就向线段树中插入这个下边线段,插入线段的权值是1;扫到一个上边,就插入权值为-1的线段。插入后,线段树动态维护当前覆盖的长度。当同一x坐标的线段都插入完成后,计算这一块的面积。
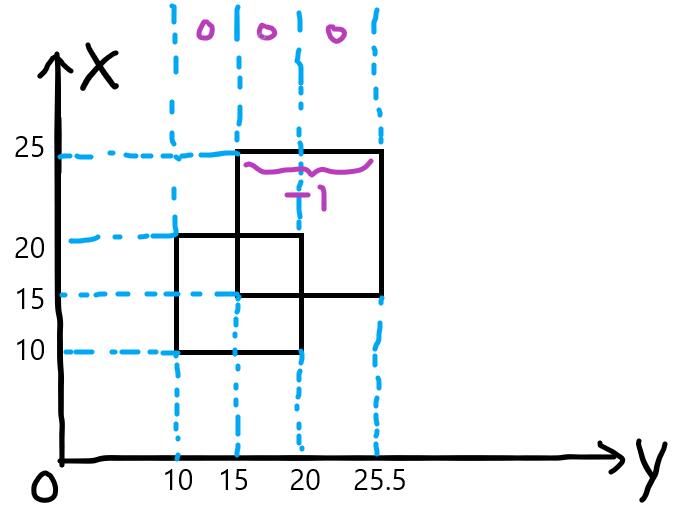
以样例为例吧。下图是样例的示意图。
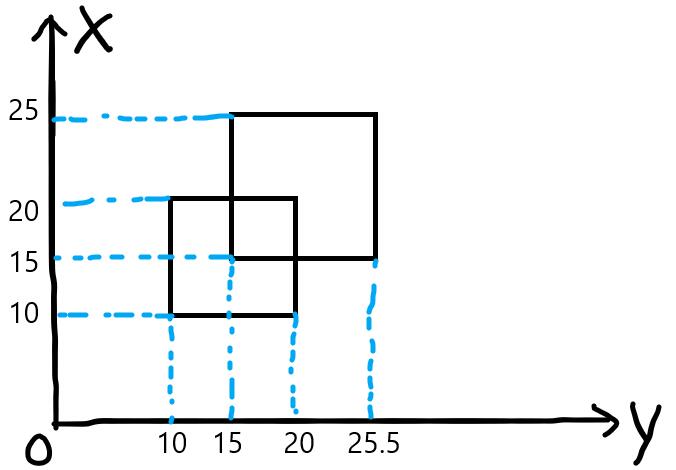
首先x=10的线段,向线段树中插入线段(10, 20)权值1,此时长度为10。
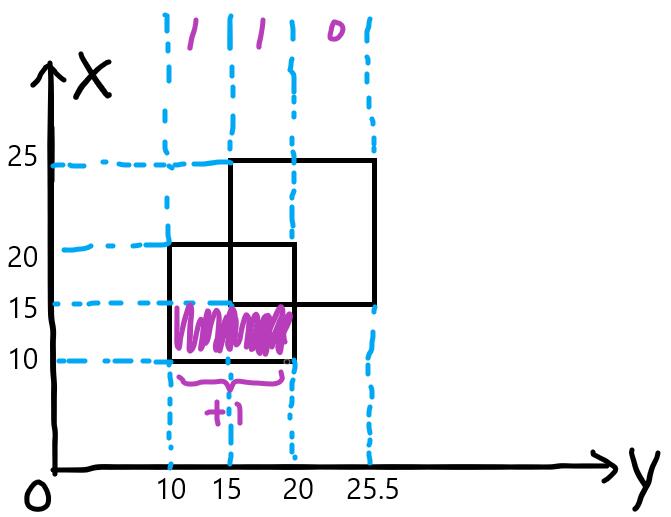
x=15的线段,向线段树中插入线段(15, 25.5)权值1,此时长度为20.5。
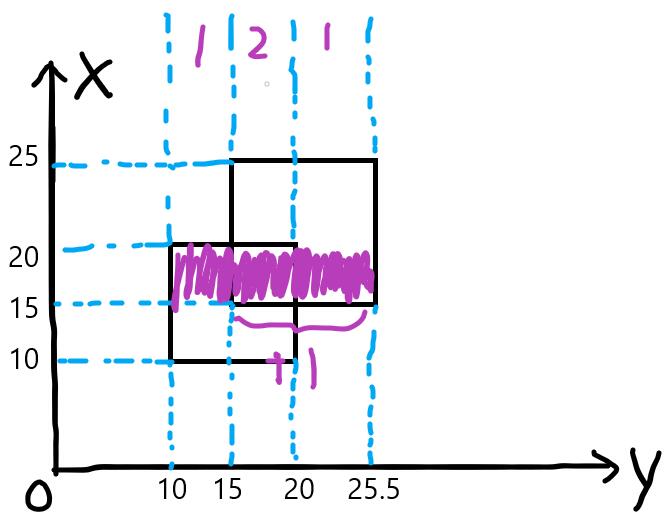
x=20的线段,向线段树中插入线段(10, 20)权值-1,此时长度为10.5。
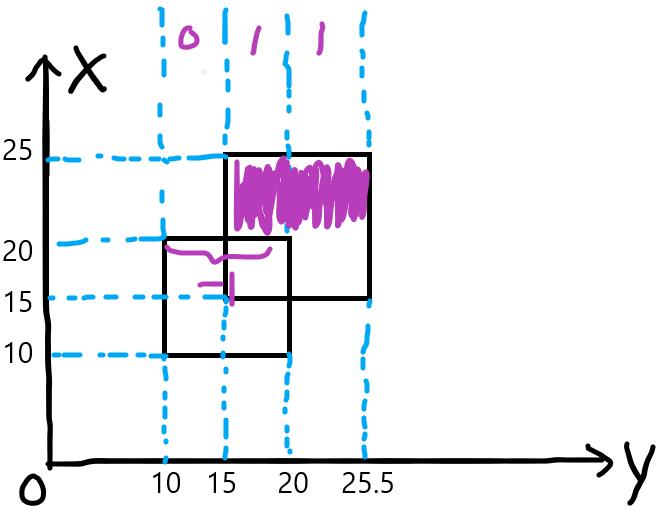
x=25的线段,向线段树中插入线段(15, 25.5)权值-1,此时长度为0。(其实这一步可以不做)
// Code by KSkun. 2018/2
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
struct Line {
double x, y1, y2;
int v;
} line[205];
inline bool cmp(Line a, Line b) {
return a.x < b.x;
}
int n, N, kase = 0;
double xa, ya, xb, yb, ans;
std::vector<double> vecy;
std::vector<double>::iterator yend;
// Segtree
#define lch o << 1
#define rch (o << 1) | 1
#define mid ((l + r) >> 1)
int val[1005];
double len[1005];
inline void callen(int o, int l, int r) {
if(val[o] > 0) {
len[o] = vecy[r - 1] - vecy[l - 1];
} else {
len[o] = len[lch] + len[rch];
}
}
inline void add(int o, int l, int r, int ll, int rr, int v) {
if(l == ll && r == rr) {
val[o] += v;
callen(o, l, r);
return;
}
if(rr <= mid) {
add(lch, l, mid, ll, rr, v);
} else if(ll >= mid) {
add(rch, mid , r, ll, rr, v);
} else {
add(lch, l, mid, ll, mid, v);
add(rch, mid, r, mid, rr, v);
}
callen(o, l, r);
}
int main() {
while(scanf("%d", &n) != EOF && n != 0) {
kase++;
ans = 0;
vecy.clear();
memset(val, 0, sizeof val);
memset(len, 0, sizeof len);
for(int i = 1; i <= n; i++) {
scanf("%lf%lf%lf%lf", &xa, &ya, &xb, &yb);
vecy.push_back(ya);
vecy.push_back(yb);
line[i].x = xa;
line[i].y1 = ya;
line[i].y2 = yb;
line[i].v = 1;
line[i + n].x = xb;
line[i + n].y1 = ya;
line[i + n].y2 = yb;
line[i + n].v = -1;
}
std::sort(vecy.begin(), vecy.end());
yend = std::unique(vecy.begin(), vecy.end());
N = yend - vecy.begin();
for(int i = 1; i <= n << 1; i++) {
line[i].y1 = std::lower_bound(vecy.begin(), yend, line[i].y1) - vecy.begin() + 1;
line[i].y2 = std::lower_bound(vecy.begin(), yend, line[i].y2) - vecy.begin() + 1;
}
std::sort(line + 1, line + (n << 1) + 1, cmp);
add(1, 1, N, line[1].y1, line[1].y2, line[1].v);
for(int i = 2; i <= n << 1; i++) {
if(line[i].x > line[i - 1].x) {
ans += len[1] * (line[i].x - line[i - 1].x);
}
add(1, 1, N, line[i].y1, line[i].y2, line[i].v);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n", kase, ans);
}
return 0;
}
题目地址:洛谷:【P3449】[POI2006]PAL-Palindromes – 洛谷
Little Johnny enjoys playing with words. He has chosen nnn palindromes (a palindrome is a wordthat reads the same when the letters composing it are taken in the reverse order, such as dad, eye orracecar for instance) then generated all n2n^2n2 possible pairs of them and concatenated the pairs intosingle words. Lastly, he counted how many of the so generated words are palindromes themselves.
However, Johnny cannot be certain of not having comitted a mistake, so he has asked you to repeatthe very same actions and to give him the outcome. Write a programme which shall perform thistask for you.
TaskWrite a programme which:
reads the palindromes given by Johnny from the standard input, determines the number of words formed out of pairs of palindromes from the input, which are palindromes themselves, writes the outcome to the standard output.
给出n个回文串s1, s2, …, sn 求如下二元组(i, j)的个数 si + sj 仍然是回文串 规模 输入串总长不超过2M bytes
输入格式:
The first line of the standard input contains a single integer n , n≥2 , denoting the number ofpalindromes given by Johnny. The following n lines contain a description of the palindromes. The (i+1)’st line contains a single positive integer ai denoting the length of i’th palindrome and apalindrome of ai small letters of English alphabet. The number ai is separated from the palindromeby a single space. The palindromes in distinct lines are distinct. The total length of all palindromesdoes not exceed 2 000 000.
输出格式:
The first and only line of the standard output should contain a single integer: the number of distinctordered pairs of palindromes which form a palindrome upon being concatenated.
输入样例#1:
6 2 aa 3 aba 3 aaa 6 abaaba 5 aaaaa 4 abba
输出样例#1:
14
感谢远航之曲提供思路,这是他的原博文bzoj 1524 [POI2006]Pal | 远航休息栈。
这个拼接成回文串的情况,肯定是较短串是较长串的前缀时成立,因此可以Trie树处理这些字符串,然后枚举每个字符串的前缀是否也在里面,在的话试着拼接一下。判断是否是回文串的方法可以用哈希处理。前串的哈希乘上哈希基的后串长次方再加后串的哈希就能完成拼接。对于每一对这样的字符串显然是反着拼也成立,统计答案是要乘2。自己和自己拼算了两次要减掉。
// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <string>
const int MO = 1e9 + 7, base = 255;
int ch[2000005][26], tot = 1;
int wrd[2000005], cnt[2000005];
int n, len[2000005], hash[2000005], bpow[2000005];
std::string str[2000005];
char strt[2000005];
long long ans = 0;
inline void insert(char* str, int id) {
int t = 1;
for(int i = 0; i < len[id]; i++) {
if(!ch[t][str[i] - 'a']) {
t = ch[t][str[i] - 'a'] = ++tot;
} else {
t = ch[t][str[i] - 'a'];
}
}
wrd[t] = id;
cnt[t]++;
}
inline int calhash(char* str, int len) {
long long res = 0;
for(int i = 0; i < len; i++) {
res = (res * base + str[i]) % MO;
}
return res;
}
int main() {
scanf("%d", &n);
bpow[0] = 1;
for(int i = 1; i < 2000005; i++) {
bpow[i] = (1ll * bpow[i - 1] * base) % MO;
}
for(int i = 1; i <= n; i++) {
scanf("%d%s", &len[i], strt);
insert(strt, i);
hash[i] = calhash(strt, len[i]);
str[i] = strt;
}
for(int i = 1; i <= n; i++) {
int u = 1;
for(int j = 0; j < len[i]; j++) {
u = ch[u][str[i][j] - 'a'];
if(wrd[u]) {
if((1ll * hash[wrd[u]] * bpow[len[i]] % MO + hash[i]) % MO ==
(1ll * hash[i] * bpow[len[wrd[u]]] % MO + hash[wrd[u]]) % MO) {
ans = ans + 1ll * cnt[u] * 2;
}
}
}
}
printf("%lld", ans - n);
return 0;
}