题目地址：洛谷：P5666 树的重心 – 洛谷 | 计算机科学教育新生态

题目描述

小简单正在学习离散数学，今天的内容是图论基础，在课上他做了如下两条笔记：

1. 一个大小为 $n$ 的树由 $n$ 个结点与 $n-1$ 条无向边构成，且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边，树将分裂为若干个子树；而在树中删去一条边（保留关联结点，下同），树将分裂为恰好两个子树。
2. 对于一个大小为 $n$ 的树与任意一个树中结点 $c$，称 $c$ 是该树的重心当且仅当在树中删去 $c$ 及与它关联的边后，分裂出的所有子树的大小均不超过 $\left\lfloor \dfrac{n}{2} \right\rfloor$（其中 $\lfloor x \rfloor$ 是下取整函数）。对于包含至少一个结点的树，它的重心只可能有 1 或 2 个。

课后老师给出了一个大小为 $n$ 的树 $S$，树中结点从 $1 \sim n$ 编号。小简单的课后作业是求出 $S$ 单独删去每条边后，分裂出的两个子树的重心编号和之和。即：

$$ \sum\limits_{(u,v) \in E} \left( \sum\limits_{1 \leq x \leq n \atop 且 x 号点是 S’_u 的重心} x + \sum\limits_{1 \leq y \leq n \atop 且 y 号点是 S’_v 的重心} y \right) $$

上式中，$E$ 表示树 $S$ 的边集，$(u,v)$ 表示一条连接 $u$ 号点和 $v$ 号点的边。$S’_u$ 与 $S’_v$​ 分别表示树 SSS 删去边 $(u,v)$ 后，$u$ 号点与 $v$ 号点所在的被分裂出的子树。

小简单觉得作业并不简单，只好向你求助，请你教教他。

题意简述

给定一棵 $n$ 个点的树，求树上每一条边 $(u,v)$ 删去后得到两个子树的所有重心编号之和。

输入输出格式

输入格式：

本题包含多组测试数据

第一行一个整数 $T$ 表示数据组数。

接下来依次给出每组输入数据，对于每组数据：

第一行一个整数 $n$ 表示树 $S$ 的大小。

接下来 $n-1$ 行，每行两个以空格分隔的整数 $u_i, v_i$​，表示树中的一条边 $(u_i,v_i)$。

输出格式：

共 $T$ 行，每行一个整数，第 $i$ 行的整数表示：第 $i$ 组数据给出的树单独删去每条边后，分裂出的两个子树的重心编号和之和。

输入输出样例

样例 #1

输入样例 #1：

2
5
1 2
2 3
2 4
3 5
7
1 2
1 3
1 4
3 5
3 6
6 7

输出样例 #1：

32
56

数据范围

表中特殊性质一栏，两个变量的含义为存在一个 $1 \sim n$ 的排列 $p_i \ (1 \leq i \leq n)$，使得：

• A：树的形态是一条链。即 $\forall 1 \leq i \lt n$，存在一条边 $(p_i, p_i + 1)$。
• B：树的形态是一个完美二叉树。即 $\forall 1 \leq i \leq \dfrac{n-1}{2}$​ ，存在两条边 $(p_i, p_{2i})$ 与 $(p_i, p_{2i+1})$。

对于所有测试点：$1 \leq T \leq 5 , 1 \leq u_i,v_i \leq n$。保证给出的图是一个树。

题解

参考资料：

• 题解 P5666 【树的重心【民间数据】】 – wucstdio 的博客 – 洛谷博客
• 题解 P5666 【树的重心】 – xht37 的洛谷博客 – 洛谷博客

可能用到的记号：

• $T(u)$：点 $u$ 对应的子树；
• $\boldsymbol{T}(u)$：点 $u$ 的所有儿子对应的子树集合；
• $\mathrm{size}(u)$：点 $u$ 对应的子树的大小；
• $\mathrm{size}(T)$：树 $T$ 的大小；
• $\mathrm{mxson}(u)$：点 $u$ 所有儿子中，对应子树最大的儿子；
• $\overline{T(u)}$：除点 $u$ 对应的子树之外，原树剩余的部分。

看到题目的第一感觉

拿到这个题目之后，第一个想法是枚举树上的每条边，其两端点对应的子树在树的 DFS 分别对应一个和最多两个区间。对于有根树而言，求子树中重心，就相当于求子树中最大儿子大小 $f(u)=\max\limits_{v \in \mathrm{son}(u)}\{ \mathrm{size}(v) \}$ 与父节点对应子树大小 $g(u)=n-\mathrm{size}(u)$ 二者中较大值的最小值 $\min\limits_{u \in \boldsymbol{V}(S)} \{ \max\{f(u),g(u)\} \}$ 对应的点 $u$。但这种想法情况众多，因为删边会影响两端点对应子树的 $f$ 值和 $g$ 值，它们的处理比较麻烦，目前为止并没能研究出来。

正难则反

接下来要介绍的是一种「正难则反」的方法，即枚举边不是好做的方法，则枚举点，考虑其作为某种情况中的重心的次数。

下文中会以如 #标记 1# 的形式进行标记以建立上下文描述与实现代码之间的联系，请合理利用标记。

普遍情况

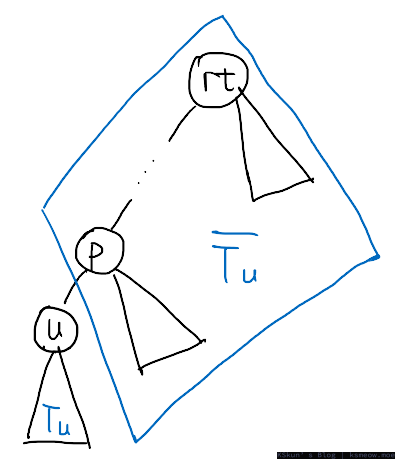
当 $u$ 不是根时，如上图，要让点 $u$ 成为某种情况下的重心，假设 $u$ 的所有儿子对应的子树 $\boldsymbol{T}(u)$ 都满足要求，只需要在除 $u$ 对应子树的部分 $\overline{T(u)}$ 删去一条边减小它的大小即可。记 $u$ 对应子树大小 $p=\mathrm{size}(u)$，$u$ 的最大儿子对应子树大小 $q=\mathrm{size}[\mathrm{mxson}(u)]$，删去一条边后从 $\overline{T(u)}$ 中移除的子树大小为 $r$。根据重心的定义，有以下条件成立：

$$ \begin{cases}
n-r-p \leq \left\lfloor \dfrac{n-r}{2} \right\rfloor, & u 的父亲对应的子树（即 \overline{T(u)} \backslash T(o)）满足重心定义, \\
q \leq \left\lfloor \dfrac{n-r}{2} \right\rfloor, & u 的最大儿子对应子树满足重心定义.
\end{cases} $$

将分母的 2 乘到另一边上，再将 $r$ 单独整理出来，可以得到下式

$$ n – 2p \leq r \leq n – 2q $$

当 $r$ 不包括 $u$ 到树根路径（即图中的链 $rt, \dots, p$）上的点时，记删掉的边中远离 $u$ 的端点为 $o$，则$r = \mathrm{size}(o)$，因此只要构建出 $\overline{T(u)}$ 所有点 $\mathrm{size}$ 值的权值线段树或权值树状数组，就能很方便地查到落在区间 $[n-2p, n-2q]$ 区间内的 $r$ 值有多少个，而这就是 $u$ 点作为重心的情况数。#标记 1#

但 $r$ 也有可能包括 $u$ 到树根路径上的点，记删掉的边为 $(o_1, o_2)$，其中 $o_1$ 离 $u$ 更近，而 $o_2$ 离 $u$ 更远（即这条边在 $u$ 到树根的链上，且 $o_1$ 比 $o_2$ 更深），此时对应的删掉的子树大小应该为 $n-\mathrm{size}(o_1)$。在上文提到的树状数组中，应当删去 $\mathrm{size}(o_2)$ 一项，而加入 $[n-\mathrm{size}(o_1)]$ 一项。这个修正可以在 DFS 计算树状数组时维护好。#标记 2#

如果每次枚举一个点 $u$ 都动态地处理出所需的树状数组，复杂度不是很优，因此可以采用预先对原树全树的 $\mathrm{size}$ 值建树状数组，之后再排除 $u$ 对应子树中被错误统计进去的答案。实现排除错误答案可以用一个 DFS 进行计算，动态地往一个树状数组里添加 $\mathrm{size}$ 值，在 DFS 进入 $u$ 的子树前记下此时的答案，$u$ 子树计算完成后再记下此时的答案，前后答案之差即为 $u$ 点的错误答案，从 $u$ 作为重心的次数里减去这一错误情况即可。在这个 DFS 中，上一段中的修正（#标记 2#）也可以同时进行。#标记 3#

接下来分析上述方法的正确性。上述方法需要假定 $u$ 的所有儿子对应的子树 $\boldsymbol{T}(u)$ 都满足 $u$ 是重心时的要求，为了实现这一要求，必须有 $n-\mathrm{size}(u) \geq \mathrm{size}[\mathrm{mxson}(u)]$ 总是成立。不妨以全树的重心为根，这样就有 $\mathrm{size}(u) \leq \lfloor n/2 \rfloor$ 总是成立，而上式同时成立。这样就能保证当 $u$ 是重心时删掉的边一定不在 $u$ 的子树中，而是在 $\overline{T(u)}$ 中，实现了统计答案的不重不漏。

而上述方法带来了一个麻烦，记树根为 $rt$，该点的答案无法如上计算，因为该点对应的 $\overline{T(rt)} = \emptyset$，需要删掉的边一定在 $rt$ 的子树中。

计算根的答案

不妨把情况分为要切掉的子树在根的最大儿子子树中和不在最大儿子子树中，分别讨论。记最大儿子子树大小为 $s_1=\mathrm{size}[\mathrm{mxson}(rt)]$，次大儿子子树大小为 $s_2$，删边后移除的子树大小为 $r$。

要切掉的子树在根的最大儿子子树中

当切掉后的最大儿子子树大小 $s’_1=s_1-r$ 仍不小于次大儿子子树大小，即 $s’_1 \geq s_2 \Rightarrow r \leq s_1 – s_2$ 时，$rt$ 仍然是此时树的重心。下面证明这一结论，已知 $s_1 \leq \lfloor n/2 \rfloor \Rightarrow 2s_1 \leq n$，要证 $s_1 – r \leq \lfloor (n-r)/2 \rfloor \Rightarrow 2s_1 \leq n + r$，由于 $r>0$，待证式显然成立。

$s’_1<s_2$ 时，原来的次大儿子子树就变成了现在的最大儿子子树，必须满足 $s_2 \leq \lfloor (n-r)/2 \rfloor$，即 $s_1 – s_2 < r \leq n – 2s_2$。

综上，要使 $rt$ 仍是树的重心，必须满足 $r \leq n-2s_2$，可以最后单独对最大儿子子树 DFS，暴力判断每个点的 $\mathrm{size}$ 值是否满足要求即可。#标记 4#

要切掉的子树不在根的最大儿子子树中

最大儿子子树必须满足 $s_1 \leq \lfloor (n-r)/2 \rfloor$，即 $r \leq n – 2s_1$。可以和上面相似地，单独 DFS 暴力统计这些子树中每个点的 $\mathrm{size}$ 值是否满足要求。#标记 5#

总结

到此为止，我们推出了本题所有情况的解法，下面整理一下思路，便于实现。

首先，由于解法中需要使用子树大小、最大儿子子树、根的次大儿子子树这些信息，可以用一个 DFS 计算出所有这些信息。有了子树大小信息，找出全树重心也不是难事。需要注意，在找出重心后，由于换根，这些信息还需要以重心为根重新计算一遍。

有了信息之后，就可以计算除了根之外的答案。用一个数组存储每个点作为重心的次数，用 DFS 计算答案。首先根据上文描述（#标记 2#），我们需要修正树状数组中当前点 $u$ 父节点的 $\mathrm{size}$ 为 $[n-\mathrm{size}(u)]$，然后查询区间落在 $[n-2\mathrm{size}(u), n-2\mathrm{size}[\mathrm{mxson}(u)]]$ 中的 $\mathrm{size}$ 值（#标记 1#）。另外为了排除错误情况，需要另开一个树状数组动态维护 $\mathrm{size}$ 值，错误情况数就是 DFS 深入儿子前后的答案之差，计算并修正答案即可（#标记 3#）。

下一步，计算根的答案。利用一个 DFS，在根的最大儿子子树中找到落在 $[1, n-2\mathrm{s_2}]$ 之内的 $\mathrm{size}$ 值数量（#标记 4#），和根的其他儿子子树中落在 $[1, n-2\mathrm{s_1}]$之内的 $\mathrm{size}$ 值数量（#标记 5#），两者之和便是根的答案。

最后，将出现次数与点的编号相乘加和就可得到最终答案。需要注意的是，答案可能过大，需要用 long long 存储与输出。

复杂度分析

上述过程中，我们使用了一共三个 DFS，其中处理子树大小等信息的 DFS 复杂度为 $O(n)$，利用树状数组求根以外点答案的 DFS 复杂度为 $O(n \log n)$，求根答案的 DFS 复杂度为 $O(n)$，因此总复杂度为 $O(n \log n)$。

代码

由于用 vector 存图，只有开 O2 能过。

// Code by KSkun, 2020/5
#include <cstdio>
#include <cctype>
#include <cstring>

#include <algorithm>
#include <utility>
#include <vector>

typedef unsigned long long LL;
typedef std::pair<int, int> PII;

using std::vector;

inline char fgc() {
	static char buf[100000], *p1 = buf, *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
		? EOF : *p1++;
}

inline LL readint() {
	register LL res = 0, neg = 1; register char c = fgc();
	for (; !isdigit(c); c = fgc()) if (c == '-') neg = -1;
	for (; isdigit(c); c = fgc()) res = res * 10 + c - '0';
	return res * neg;
}

inline char readsingle() {
	char c;
	while (!isgraph(c = fgc())) {}
	return c;
}

const int MAXN = 300005;

// siz: 子树大小, mx_ch: 最大子树, mx2_1ch: 树根的次大子树, cnt: 作重心的次数
int T, n, ct, siz[MAXN], mx_ch[MAXN], mx2_1ch, cnt[MAXN];
vector<int> G[MAXN];

// 树状数组
class BinaryIndexedTree {
private:
	int n, dat[MAXN];
	int lowbit(int x) {
		return x & -x;
	}
public:
	void init(int _n) {
		n = _n;
		memset(dat, 0, sizeof(dat));
	}

	void add(int idx, int val) {
		if (idx <= 0) return;
		for (int i = idx; i <= n; i += lowbit(i)) dat[i] += val;
	}

	int query(int idx) {
		if (idx <= 0) return 0;
		int res = 0;
		for (int i = idx; i > 0; i -= lowbit(i)) res += dat[i];
		return res;
	}
} tree1, tree2;

// DFS 处理全树重心、子树大小、最大子树和树根的次大子树
void dfs_siz(int u, int par) {
	siz[u] = 1;
	mx_ch[u] = 0;
	for (int v : G[u]) {
		if (v == par) continue;
		dfs_siz(v, u);
		siz[u] += siz[v];
		if (siz[mx_ch[u]] <= siz[v]) {
			if (u == ct) mx2_1ch = mx_ch[u];
			mx_ch[u] = v;
		} else if (u == ct && siz[mx2_1ch] <= siz[v]) {
			mx2_1ch = v;
		}
	}
	if (siz[mx_ch[u]] <= n / 2 && n - siz[u] <= n / 2) ct = u;
}

// DFS 计算根之外点的次数
void dfs_cal(int u, int par) {
	tree1.add(siz[par], -1); // 修正到根路径上各边两端子树大小 #标记 2#
	tree1.add(n - siz[u], 1);
	cnt[u] = tree1.query(n - 2 * siz[mx_ch[u]]) - tree1.query(n - 2 * siz[u] - 1); // #标记 1#
	int bef = tree2.query(n - 2 * siz[mx_ch[u]]) - tree2.query(n - 2 * siz[u] - 1); // #标记 3# DFS 进入子树前
	for (int v : G[u]) {
		if (v == par) continue;
		dfs_cal(v, u);
	}
	tree2.add(siz[u], 1);
	int aft = tree2.query(n - 2 * siz[mx_ch[u]]) - tree2.query(n - 2 * siz[u] - 1);
	cnt[u] -= aft - bef; // 用算子树前后 tree2 值的变化来计算子树中算入的情况 #标记 3#
	tree1.add(siz[par], 1); // 消除修正的影响 #标记 2#
	tree1.add(n - siz[u], -1);
}

// DFS 处理树根的方案
void dfs_rt(int u, int par, int lim) {
	if (siz[u] <= lim) cnt[ct]++;
	for (int v : G[u]) {
		if (v == par) continue;
		dfs_rt(v, u, lim);
	}
}

int main() {
	T = readint();
	while (T--) {
		// 输入
		n = readint();
		for (int i = 1; i <= n; i++) G[i].clear();
		for (int i = 1, u, v; i <= n - 1; i++) {
			u = readint(); v = readint();
			G[u].push_back(v);
			G[v].push_back(u);
		}

		// 预处理子树大小的权值树状数组
		dfs_siz(1, 0); // 计算重心
		dfs_siz(ct, 0); // 以重心为根计算树信息
		tree1.init(n);
		for (int i = 1; i <= n; i++) tree1.add(siz[i], 1);
		tree2.init(n); // 计算除根之外点的次数
		dfs_cal(ct, 0);
		
		// 计算树根作重心的次数
		cnt[ct] = 0;
		dfs_rt(mx_ch[ct], ct, n - 2 * siz[mx2_1ch]); // 在根的最大子树中删边 #标记 4#
		for (int ch : G[ct]) {
			if (ch == mx_ch[ct]) continue;
			dfs_rt(ch, ct, n - 2 * siz[mx_ch[ct]]); // 在根的其他子树中删边 #标记 5#
		}

		LL ans = 0;
		for (int i = 1; i <= n; i++) ans += (LL) i * cnt[i];
		printf("%lld\n", ans);
	}
	return 0;
}