题目地址：洛谷：【P4001】[BJOI2006]狼抓兔子 – 洛谷、BZOJ：Problem 1001. — [BeiJing2006]狼抓兔子

题目描述

现在小朋友们最喜欢的”喜羊羊与灰太狼”,话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

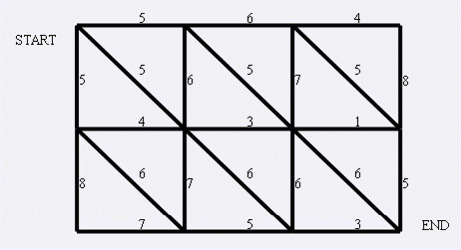
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入输出格式

输入格式：
第一行为N,M.表示网格的大小，N,M均小于等于1000.
接下来分三部分
第一部分共N行，每行M-1个数，表示横向道路的权值.
第二部分共N-1行，每行M个数，表示纵向道路的权值.
第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输出格式：
输出一个整数，表示参与伏击的狼的最小数量.

输入输出样例

输入样例#1：

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

输出样例#1：

14

题解

网络流

我们可以直接按照图示建立网络，求最小割。Dinic跑是很快的。

对偶图

这有个讲解对偶图的ppt：点击下载
然后我们可以利用对偶图的性质，建立对偶图，求S到T的最短路，即为最小割。这样来做点数边数能够变小，避免了空间爆炸的情况。
下面的代码中，建图的规律是第一行右上三角形的编号为1~m-1，左下三角形的编号为m~2m-2，底下以此类推。需要判断越界的面属于S还是T。

代码

网络流

// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>

#include <algorithm>
#include <queue>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF 
        : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    register char c = fgc();
    while(c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MAXN = 2000005, INF = 1e9;

struct Edge {
    int to, cap, nxt;
} gra[MAXN * 5];
int head[MAXN], tot;

inline void addedge(int u, int v, int cap) {
    gra[tot] = Edge {v, cap, head[u]}; head[u] = tot++;
    gra[tot] = Edge {u, cap, head[v]}; head[v] = tot++;
}

int level[MAXN];

inline bool bfs(int s, int t) {
    memset(level, -1, sizeof(level));
    std::queue<int> que;
    level[s] = 0; que.push(s);
    while(!que.empty()) {
        int u = que.front(); que.pop();
        for(int i = head[u]; ~i; i = gra[i].nxt) {
            int v = gra[i].to;
            if(level[v] == -1 && gra[i].cap > 0) {
                level[v] = level[u] + 1;
                if(v == t) return true;
                que.push(v);
            }
        }
    }
    return level[t] != -1;
}

int cur[MAXN];

inline int dfs(int u, int t, int left) {
    if(u == t || left <= 0) return left;
    int flow = 0;
    for(int &i = cur[u]; ~i; i = gra[i].nxt) {
        int v = gra[i].to;
        if(gra[i].cap > 0 && level[v] == level[u] + 1) {
            int d = dfs(v, t, std::min(left, gra[i].cap));
            if(d > 0) {
                flow += d; left -= d;
                gra[i].cap -= d; gra[i ^ 1].cap += d;
                if(left <= 0) break;
            }
        }
    }
    return flow;
}

inline int dinic(int s, int t) {
    int flow = 0;
    while(bfs(s, t)) {
        memcpy(cur, head, sizeof(head));
        int f;
        while(f = dfs(s, t, INF)) {
            flow += f;
        }
    }
    return flow;
}

int n, m, t;

int main() {
    memset(head, -1, sizeof(head));
    n = readint(); m = readint();
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j < m; j++) {
            t = readint();
            addedge((i - 1) * m + j, (i - 1) * m + j + 1, t);
        }
    }
    for(int i = 1; i < n; i++) {
        for(int j = 1; j <= m; j++) {
            t = readint();
            addedge((i - 1) * m + j, i * m + j, t);
        }
    }
    for(int i = 1; i < n; i++) {
        for(int j = 1; j < m; j++) {
            t = readint();
            addedge((i - 1) * m + j, i * m + j + 1, t);
        }
    }
    printf("%d", dinic(1, n * m));
    return 0;
}

对偶图

参考资料：【BJOI2006】狼抓兔子 – flow丶 – 博客园

// Code by KSkun, 2018/4
#include <cstdio>
#include <cstring>

#include <queue>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF 
        : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1;
    register char c = fgc();
    while(c < '0' || c > '9') {
        if(c == '-') neg = -1;
        c = fgc();
    }
    while(c >= '0' && c <= '9') {
        res = res * 10 + c - '0';
        c = fgc();
    }
    return res * neg;
}

const int MAXN = 2000005, INF = 1e9;

struct Edge {
    int to, w, nxt;
} gra[MAXN << 2];
int head[MAXN], tot;

inline void addedge(int u, int v, int w) {
    gra[tot] = Edge {v, w, head[u]}; head[u] = tot++;
    gra[tot] = Edge {u, w, head[v]}; head[v] = tot++;
}

int dis[MAXN];
bool inque[MAXN];

inline void spfa(int s) {
    std::queue<int> que;
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0; inque[s] = true;
    que.push(s);
    while(!que.empty()) {
        int u = que.front(); que.pop(); inque[u] = false;
        for(int i = head[u]; ~i; i = gra[i].nxt) {
            int v = gra[i].to;
            if(dis[v] > dis[u] + gra[i].w) {
                dis[v] = dis[u] + gra[i].w;
                if(!inque[v]) {
                    inque[v] = true;
                    que.push(v);
                }
            }
        }
    }
}

int n, m, t, S, T;

int main() {
    memset(head, -1, sizeof(head));
    n = readint(); m = readint(); 
    S = 0; T = (n - 1) * (m - 1) * 2 + 1;
    int u = 1;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j < m; j++) {
            t = readint();
            int v = u - (m - 1), u1 = u, v1 = v;
            if(v <= S) v1 = S;
            if(u >= T) u1 = T;
            addedge(u1, v1, t);
            u++;
        }
        u += m - 1;
    }
    u = m;
    for(int i = 1; i < n; i++) {
        for(int j = 1; j <= m; j++) {
            t = readint();
            int v = u - m, u1 = u, v1 = v;
            if(v <= 2 * (i - 1) * (m - 1)) v1 = T;
            if(u > 2 * i * (m - 1)) u1 = S; 
            addedge(u1, v1, t);
            u++;
        }
        u += m - 2;
    }
    u = 1;
    for(int i = 1; i < n; i++) {
        for(int j = 1; j < m; j++) {
            t = readint();
            addedge(u, u + m - 1, t);
            u++;
        }
        u += m - 1;
    }
    spfa(S);
    printf("%d", dis[T]);
    return 0;
}