[CSP-S2 2019]Emiya 家今天的饭 题解
题目地址:洛谷:P5664 Emiya 家今天的饭 – 洛谷 | 计算机科学教 …
May all the beauty be blessed.
题目地址:Codeforces:Problem – 2C – Codeforces、洛谷:CF2C Commentator problem – 洛谷 | 计算机科学教育新生态
The Olympic Games in Bercouver are in full swing now. Here everyone has their own objectives: sportsmen compete for medals, and sport commentators compete for more convenient positions to give a running commentary. Today the main sport events take place at three round stadiums, and the commentator’s objective is to choose the best point of observation, that is to say the point from where all the three stadiums can be observed. As all the sport competitions are of the same importance, the stadiums should be observed at the same angle. If the number of points meeting the conditions is more than one, the point with the maximum angle of observation is prefered.
Would you, please, help the famous Berland commentator G. Berniev to find the best point of observation. It should be noted, that the stadiums do not hide each other, the commentator can easily see one stadium through the other.
给三个圆,求符合从该点处观察三个圆的可视角度是相同的这样的点。若有多个点,则输出可视角度最大的那个。若无解,输出为空。
可视角度是指从圆外一点作该圆的两条切线,切线所夹的角的角度。
输入格式:
The input data consists of three lines, each of them describes the position of one stadium. The lines have the format x, y, r, where (x, y) are the coordinates of the stadium’s center ( - 10^3 ≤ x, y ≤ 10^3), and r (1 ≤ r ≤ 10^3) is its radius. All the numbers in the input data are integer, stadiums do not have common points, and their centers are not on the same line.
输出格式:
Print the coordinates of the required point with five digits after the decimal point. If there is no answer meeting the conditions, the program shouldn’t print anything. The output data should be left blank.
输入样例#1:
0 0 10 60 0 10 30 30 10
输出样例#1:
30.00000 0.00000
绘图软件:GeoGebra
首先根据可视角度的定义,我们可以作出一个示意图,如图中的$\angle \alpha$就是P观察圆O的可视角度。
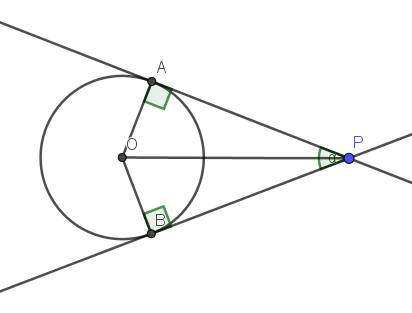
由于圆的半径是固定的,可以观察出,P到O的距离决定了可视角度的大小。同时还可以得到如下结论:要使一个点观察两个圆的可视角度相同,则该点到两圆圆心的距离之比等于两圆的半径之比。
那么思路就很明确了,即找到到三个圆圆心距离之比等于三个圆半径之比这样的一个点即可。问题是怎么求出这个点。
在高中解析几何中,接触到了这样的一类题目:P到两定点距离之比为一不为1的正实数,求P点的轨迹。实际上,P点的轨迹是一个圆,这类圆又被称作阿波罗尼斯圆。不过这道题不需要使用阿氏圆的性质,我们只需要知道到两圆圆心的距离之比等于两圆的半径之比的点的轨迹是一个圆。取三个圆中的某两个出来,可以列出一个阿氏圆的方程,而写出两个方程之后,可以通过联立解出圆的交点。如果没有交点,说明没有符合要求的点;如果交点有1个,输出即可;如果交点有2个,选择到圆心距离最近的那个,因为这个的可视角度最大。
此外,还要考虑到如果有两个圆半径相等,此时距离的比值为1,则P点的轨迹是两圆心连线的中垂线。如果三个圆半径都相同,则是两两中垂线的交点;如果只有两个圆半径相等,另外一个不相等,则联立中垂线和阿氏圆方程求直线和圆的交点即可。
求解圆圆交点可以先令圆的一般式相减得到交点所在直线,再求线圆交点。线圆交点在实现时,我使用了消$y$解二次方程的方法。线线交点也是消$y$解方程。由于实现中采用了斜截式表示直线,在操作时会将全局坐标旋转一个小角度,来避免斜率不存在的情况。代码中看不懂的一大堆式子多半是解方程后化简为某一个方便表示的形式后的式子,在下面会展示一部分过程。
计算线线交点的方法:
$$ \begin{cases} y = k_1x + m_1 \\ y = k_2x + m_2 \end{cases} \Rightarrow x = \frac{m_2 – m_1}{k_1 – k_2} $$
计算线圆交点的方法:
$$ \begin{cases} y = kx + m \\ (x-x_0)^2+(y-y_0)^2=r^2 \end{cases} \Rightarrow (1+k^2)x^2 + 2[k(m-y_0)-x_0]x + x^2 + (m-y_0)^2 – r^2 = 0 $$
然后运用求根公式解上述方程即可。
计算圆圆交点的方法:
$$ \begin{cases} (x-x_1)^2+(y-y_1)^2=r_1^2 \\ (x-x_2)^2+(y-y_2)^2=r_2^2 \end{cases} $$
上式减下式得到交点所在的直线方程
$$ y = \frac{x_1-x_2}{y_2-y_1}x + \frac{r_1^2-r_2^2+x_2^2-x_1^2+y_2^2-y_1^2}{2(y_2-y_1)} $$
将其代入任一圆的方程,解出线圆交点即可。
计算点点阿氏圆的方法:
假设到点$\mathrm{A}(x_1, y_1)$和到点$\mathrm{B}(x_2, y_2)$的距离之比为$k$,则
$$ \frac{\sqrt{(x-x_1)^2+(y-y_1)^2}}{\sqrt{(x-x_2)^2+(y-y_2)^2}} = k $$
化简得
$$ \left(x-\frac{x_1-k^2x_2}{1-k^2}\right)^2 + \left(y-\frac{y_1-k^2y_2}{1-k^2}\right)^2 = r_0^2 $$
令阿氏圆的圆心为$(x_0, y_0)$,则有
$$ x_0 = \frac{x_1-k^2x_2}{1-k^2}, y_0 = \frac{y_1-k^2y_2}{1-k^2}, r_0 = \frac{k^2(x_2^2+y_2^2) – (x_1^2+y_1^2)}{1-k^2}+x_0^2+y_0^2 $$
// Code by KSkun, 2019/6
#include <cstdio>
#include <cmath>
#include <algorithm>
const double EPS = 1e-8;
const double D_ANG = 1e-4;
inline int dcmp(double x) {
if(fabs(x) < EPS) return 0;
else return x < 0 ? -1 : 1;
}
struct Vector {
double x, y;
Vector operator+(const Vector &rhs) const {
return Vector {x + rhs.x, y + rhs.y};
}
Vector operator-(const Vector &rhs) const {
return Vector {x - rhs.x, y - rhs.y};
}
Vector operator*(const double &rhs) const {
return Vector {x * rhs, y * rhs};
}
Vector operator/(const double &rhs) const {
return Vector {x / rhs, y / rhs};
}
Vector getVertical() const {
return Vector {y, -x};
}
};
inline double dot(Vector a, Vector b) {
return a.x * b.x + a.y * b.y;
}
inline double length(Vector x) {
return sqrt(dot(x, x));
}
inline double angle(Vector a, Vector b) {
return acos(dot(a, b) / length(a) / length(b));
}
inline bool collinear(Vector a, Vector b) {
return dcmp(a.y * b.x - a.x * b.y) == 0;
}
inline Vector rotate(Vector v, double ang) {
return Vector {v.x * cos(ang) - v.y * sin(ang), v.x * sin(ang) + v.y * cos(ang)};
}
typedef Vector Point;
struct Line {
double k, m; // 斜截式
};
inline Line getLine(Point a, Point b) {
double k = (b.y - a.y) / (b.x - a.x), m = a.y - k * a.x;
return Line {k, m};
}
inline Line getPerpendicular(Point a, Point b) {
Point m = (a + b) / 2;
Line t = getLine(a, b);
t.k = -1 / t.k;
t.m = m.y - t.k * m.x;
return t;
}
inline Point intersection(Line a, Line b) {
double x = (b.m - a.m) / (a.k - b.k);
return Point {x, x * a.k + a.m};
}
inline int intersection(Line a, Point o, double r, Point &p1, Point &p2) {
double A = a.k * a.k + 1, B = 2 * a.k * (a.m - o.y) - 2 * o.x,
C = o.x * o.x + (a.m - o.y) * (a.m - o.y) - r * r;
double delta = B * B - 4 * A * C;
if(dcmp(delta) < 0) return 0;
else if(dcmp(delta) == 0) {
p1.x = -B / 2 / A; p1.y = p1.x * a.k + a.m;
return 1;
} else {
p1.x = (-B + sqrt(delta)) / 2 / A; p1.y = p1.x * a.k + a.m;
p2.x = (-B - sqrt(delta)) / 2 / A; p2.y = p2.x * a.k + a.m;
return 2;
}
}
inline Line intersection(Point o1, double r1, Point o2, double r2) {
double k = (o1.x - o2.x) / (o2.y - o1.y),
m = (r1 * r1 - r2 * r2 + o2.x * o2.x - o1.x * o1.x + o2.y * o2.y - o1.y * o1.y) / 2 / (o2.y - o1.y);
return Line {k, m};
}
inline int intersection(Point o1, double r1, Point o2, double r2, Point &p1, Point &p2) {
Line inter = intersection(o1, r1, o2, r2);
return intersection(inter, o1, r1, p1, p2);
}
inline bool parallel(Line a, Line b) {
return dcmp(a.k - b.k) == 0;
}
inline void getApollonius(Point a, Point b, double k, Point &o, double &r) {
double xon = (a.x - k * k * b.x) / (1 - k * k), yon = (a.y - k * k * b.y) / (1 - k * k),
ron = sqrt((k * k * (b.x * b.x + b.y * b.y) - (a.x * a.x + a.y * a.y)) / (1 - k * k) + xon * xon + yon * yon);
o = Point {xon, yon};
r = ron;
}
Point o[5];
double r[5];
int main() {
for(int i = 1; i <= 3; i++) {
scanf("%lf%lf%lf", &o[i].x, &o[i].y, &r[i]);
o[i] = rotate(o[i], D_ANG); // 预先绕坐标原点转过一个小角度
}
if(dcmp(r[1] - r[2]) == 0 && dcmp(r[2] - r[3]) == 0) { // 三个圆半径相等的情况
Line a = getPerpendicular(o[1], o[2]), b = getPerpendicular(o[2], o[3]);
if(parallel(a, b)) return 0;
Point inter = intersection(a, b);
inter = rotate(inter, -D_ANG);
printf("%.5lf %.5lf", inter.x, inter.y);
return 0;
}
if(dcmp(r[2] - r[3]) == 0) {
std::swap(o[1], o[3]); std::swap(r[1], r[3]);
}
if(dcmp(r[1] - r[3]) == 0) {
std::swap(o[2], o[3]); std::swap(r[2], r[3]);
}
if(dcmp(r[1] - r[2]) == 0) { // 有两个圆半径相等的情况
Line a = getPerpendicular(o[1], o[2]);
Point p1, p2, oa; double ra;
getApollonius(o[1], o[3], r[1] / r[3], oa, ra);
int res = intersection(a, oa, ra, p1, p2);
if(res == 0) return 0;
else if(res == 1) {
p1 = rotate(p1, -D_ANG);
printf("%.5lf %.5lf", p1.x, p1.y);
} else {
double l1 = length(p1 - o[1]), l2 = length(p2 - o[1]);
p1 = rotate(p1, -D_ANG);
p2 = rotate(p2, -D_ANG);
if(dcmp(l1 - l2) <= 0) printf("%.5lf %.5lf", p1.x, p1.y);
else printf("%.5lf %.5lf", p2.x, p2.y);
}
} else { // 三个圆半径都不相等的情况
Point oa1, oa2; double ra1, ra2;
getApollonius(o[1], o[2], r[1] / r[2], oa1, ra1);
getApollonius(o[1], o[3], r[1] / r[3], oa2, ra2);
Point p1, p2;
int res = intersection(oa1, ra1, oa2, ra2, p1, p2);
if(res == 0) return 0;
else if(res == 1) {
p1 = rotate(p1, -D_ANG);
printf("%.5lf %.5lf", p1.x, p1.y);
} else {
double l1 = length(p1 - o[1]), l2 = length(p2 - o[1]);
p1 = rotate(p1, -D_ANG);
p2 = rotate(p2, -D_ANG);
if(dcmp(l1 - l2) <= 0) printf("%.5lf %.5lf", p1.x, p1.y);
else printf("%.5lf %.5lf", p2.x, p2.y);
}
}
return 0;
}
题目地址:洛谷:【P3232】[HNOI2013]游走 – 洛谷、BZOJ:Problem 3143. — [Hnoi2013]游走
一个无向连通图,顶点从1编号到N,边从1编号到M。 小Z在该图上进行随机游走,初始时小Z在1号顶点,每一步小Z以相等的概率随机选 择当前顶点的某条边,沿着这条边走到下一个顶点,获得等于这条边的编号的分数。当小Z 到达N号顶点时游走结束,总分为所有获得的分数之和。 现在,请你对这M条边进行编号,使得小Z获得的总分的期望值最小。
输入格式:
第一行是正整数N和M,分别表示该图的顶点数 和边数,接下来M行每行是整数u,v(1<=u,v<=N),表示顶点u与顶点v之间存在一条边。
输入保证30%的数据满足N<=10,100%的数据满足2<=N<=500且是一个无向简单连通图。
输出格式:
仅包含一个实数,表示最小的期望值,保留3位小数。
输入样例#1:
3 3 2 3 1 2 1 3
输出样例#1:
3.333
边(1,2)编号为1,边(1,3)编号2,边(2,3)编号为3。
显然,如果我们知道经过每一条边的期望经过次数,那么贪心地按期望从大到小安排编号就好了。考虑如何求经过边的期望,边$(u, v)$的期望$\mathrm{E}(u, v)$是
$$ \mathrm{E}(u, v) = \frac{\mathrm{E}(u)}{deg_u} + \frac{\mathrm{E}(v)}{deg_v} $$
其中$deg_u$表示$u$的度数。我们把问题转化成如何求经过$u$点的期望$\mathrm{E}(u)$了。
这里我们考虑使用高斯消元解方程组的思路求解,对于每一个点,可以列出如下方程
$$ \mathrm{E}(u) = \sum_{(u, v) \in G, v \neq n} \frac{\mathrm{E}(v)}{deg_v} $$
移项后即可得到适合高斯消元的式子。对于$1$点,令高消方程的等号右边为$1$即可,这是让$1$强制至少经过1次。
复杂度$O(n^3)$。
// Code by KSkun, 2018/7
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <functional>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
register char c;
while(!isgraph(c = fgc())) {}
return c;
}
const int MAXN = 505;
int n, m, deg[MAXN];
double mat[MAXN][MAXN];
inline void gauss() {
for(int i = 1; i < n; i++) {
int k = i;
for(int j = i + 1; j < n; j++) {
if(fabs(mat[k][i]) < fabs(mat[j][i])) k = j;
}
if(k != i) {
for(int j = 1; j < n + 1; j++) {
std::swap(mat[k][j], mat[i][j]);
}
}
for(int j = 1; j < n; j++) {
if(j == i) continue;
double r = mat[j][i] / mat[i][i];
for(int k = 1; k < n + 1; k++) {
mat[j][k] -= r * mat[i][k];
}
}
}
for(int i = 1; i < n; i++) mat[i][n] /= mat[i][i];
}
std::vector<int> gra[MAXN];
struct Edge {
int u, v;
double prob;
inline bool operator>(const Edge &rhs) const {
return prob > rhs.prob;
}
} edges[MAXN * MAXN];
int main() {
n = readint(); m = readint();
for(int i = 1, u, v; i <= m; i++) {
u = readint(); v = readint();
deg[u]++; deg[v]++;
edges[i] = Edge {u, v};
gra[u].push_back(v); gra[v].push_back(u);
}
for(int i = 1; i < n; i++) {
mat[i][i] = 1;
for(int j = 0; j < gra[i].size(); j++) {
int v = gra[i][j];
if(v == n) continue;
mat[i][v] = -1.0 / deg[v];
}
}
mat[1][n] = 1;
gauss();
for(int i = 1; i <= m; i++) {
edges[i].prob = mat[edges[i].u][n] / deg[edges[i].u] + mat[edges[i].v][n] / deg[edges[i].v];
}
std::sort(edges + 1, edges + m + 1, std::greater<Edge>());
double ans = 0;
for(int i = 1; i <= m; i++) {
ans += i * edges[i].prob;
}
printf("%.3lf", ans);
return 0;
}
题目地址:洛谷:【P2485】[SDOI2011]计算器 – 洛谷、BZOJ:Problem 2242. — [SDOI2011]计算器
你被要求设计一个计算器完成以下三项任务:
1、给定y、z、p,计算y^z mod p 的值;
2、给定y、z、p,计算满足xy ≡z(mod p)的最小非负整数x;
3、给定y、z、p,计算满足y^x ≡z(mod p)的最小非负整数x。
为了拿到奖品,全力以赴吧!
输入格式:
输入文件calc.in 包含多组数据。
第一行包含两个正整数T、K,分别表示数据组数和询问类型(对于一个测试点内的所有数据,询问类型相同)。
以下T 行每行包含三个正整数y、z、p,描述一个询问。
输出格式:
输出文件calc.out 包括T 行.
对于每个询问,输出一行答案。
对于询问类型2 和3,如果不存在满足条件的,则输出“Orz, I cannot find x!”。
输入样例#1:
3 1 2 1 3 2 2 3 2 3 3
输出样例#1:
2 1 2
输入样例#2:
3 2 2 1 3 2 2 3 2 3 3
输出样例#2:
2 1 0
输入样例#3:
4 3 2 1 3 2 2 3 2 3 3 2 4 3
输出样例#3:
0 1 Orz, I cannot find x! 0
【数据规模和约定】
对于100%的数据,1<=y,z,p<=10^9,为质数,1<=T<=10。
$K=1$快速幂。
$K=2$时,考虑展开该式,$xy \equiv z \pmod{p} \Leftrightarrow xy + kp = z$,贝祖等式有解的条件是$\gcd(y, p)|z$,判一下有无解然后扩欧或费马小定理解决一下就好。
$K=3$时裸BSGS板,需要注意的是,要特判$y = 0$的情况。
// Code by KSkun, 2018/7
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cmath>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = (res << 1) + (res << 3) + c - '0';
return res * neg;
}
inline LL fpow(LL n, LL k, LL p) {
LL res = 1; n %= p;
for(; k; k >>= 1) {
if(k & 1) res = res * n % p;
n = n * n % p;
}
return res;
}
inline LL gcd(LL a, LL b) {
if(!b) return a;
return gcd(b, a % b);
}
const int MO = 611977, MAXN = 1000005;
struct LinkedHashMap {
int head[MO + 5], key[MAXN], val[MAXN], nxt[MAXN], tot;
inline void clear() {
tot = 0; memset(head, -1, sizeof(head));
}
LinkedHashMap() {
clear();
}
inline void insert(int k, int v) {
int idx = k % MO;
for(int i = head[idx]; ~i; i = nxt[i]) {
if(key[i] == k) {
val[i] = v; return;
}
}
key[tot] = k; val[tot] = v; nxt[tot] = head[idx]; head[idx] = tot++;
}
inline int operator[](const int &k) const {
int idx = k % MO;
for(int i = head[idx]; ~i; i = nxt[i]) {
if(key[i] == k) return val[i];
}
return -1;
}
} x;
inline LL bsgs(LL a, LL b, LL p) {
a %= p; b %= p;
if(a == 0) return b == 0 ? 1 : -1;
if(b == 1) return 0;
x.clear(); x.insert(1, 0);
LL m = ceil(sqrt(p - 1)), inv = fpow(a, p - m - 1, p);
for(LL i = 1, e = 1; i < m; i++) {
e = e * a % p;
if(x[e] == -1) x.insert(e, i);
}
for(LL i = 0; i < m; i++) {
LL res = x[b];
if(res != -1) return i * m + res;
b = b * inv % p;
}
return -1;
}
int T, K;
int main() {
T = readint(); K = readint();
while(T--) {
LL y = readint(), z = readint(), p = readint();
if(K == 1) {
printf("%lld\n", fpow(y, z, p));
} else if(K == 2) {
LL g = gcd(y, p);
if(z % g) puts("Orz, I cannot find x!");
else printf("%lld\n", fpow(y * fpow(z, p - 2, p) % p, p - 2, p));
} else {
LL res = bsgs(y, z, p);
if(res == -1) puts("Orz, I cannot find x!");
else printf("%lld\n", res);
}
}
return 0;
}