[HAOI2007]反素数 题解
题目地址:洛谷:【P1463】[HAOI2007]反素数 – 洛谷、BZOJ: …
May all the beauty be blessed.
题目地址:洛谷:【P2327】[SCOI2005]扫雷 – 洛谷、BZOJ:Problem 1088. — [SCOI2005]扫雷Mine
相信大家都玩过扫雷的游戏。那是在一个 n×m 的矩阵里面有一些雷,要你根据一些信息找出雷来。万圣节到了,“余”人国流行起了一种简单的扫雷游戏,这个游戏规则和扫雷一样,如果某个格子没有雷,那么它里面的数字表示和它8连通的格子里面雷的数目。现在棋盘是 n×2 的,第一列里面某些格子是雷,而第二列没有雷,如下图:
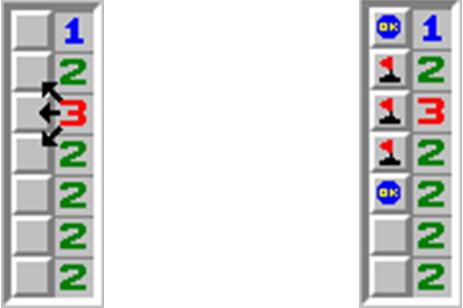
由于第一列的雷可能有多种方案满足第二列的数的限制,你的任务即根据第二列的信息确定第一列雷有多少种摆放方案。
输入格式:
第一行为N,第二行有N个数,依次为第二列的格子中的数。(1<= N <= 10000)
输出格式:
一个数,即第一列中雷的摆放方案数。
输入样例#1:
2 1 1
输出样例#1:
2
这道题的解法很多很多,我最开始的想法是存6位状压递推[eq]O(n)[/eq]解,然后特判[eq]n \leq 6[/eq]的情况。
实际上我们发现只需要枚举第一位有没有雷,剩下的位置都唯一确定了,因为一个位置有没有雷可以通过上个位置的数值减去上个位置和上上个位置的雷数得到。也就是说,方案数不会超过2,因此我们枚举第一个位置有没有雷,通过模拟计算下面的情况,如果这个位置要求的雷数非0或1则方案失败。每模拟成功一次计算一个方案。注意模拟的时候要判断末尾是否满足,可以多填一位,再判断n+1位是否有雷多出来了。模拟的复杂度也是[eq]O(n)[/eq]的。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(!isdigit(c)) {
if(c == '-') neg = -1;
c = fgc();
}
while(isdigit(c)) {
res = (res << 1) + (res << 3) + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 10005;
int n, a[MAXN], has[MAXN];
inline bool cal() {
for(int i = 2; i <= n + 1; i++) {
has[i] = a[i - 1] - has[i - 1] - has[i - 2];
if(has[i] != 0 && has[i] != 1) return false;
if(i == n + 1 && has[i] != 0) return false;
}
return true;
}
int main() {
n = readint();
for(int i = 1; i <= n; i++) {
a[i] = readint();
}
int ans = 0;
if(cal()) ans++;
memset(has, 0, sizeof(has));
has[1] = 1;
if(cal()) ans++;
printf("%d", ans);
return 0;
}
题目地址:洛谷:【P2059】[JLOI2013]卡牌游戏 – 洛谷、BZOJ:Problem 3191. — [JLOI2013]卡牌游戏
N个人坐成一圈玩游戏。一开始我们把所有玩家按顺时针从1到N编号。首先第一回合是玩家1作为庄家。每个回合庄家都会随机(即按相等的概率)从卡牌堆里选择一张卡片,假设卡片上的数字为X,则庄家首先把卡片上的数字向所有玩家展示,然后按顺时针从庄家位置数第X个人将被处决即退出游戏。然后卡片将会被放回卡牌堆里并重新洗牌。被处决的人按顺时针的下一个人将会作为下一轮的庄家。那么经过N-1轮后最后只会剩下一个人,即为本次游戏的胜者。现在你预先知道了总共有M张卡片,也知道每张卡片上的数字。现在你需要确定每个玩家胜出的概率。
这里有一个简单的例子:
例如一共有4个玩家,有四张卡片分别写着3,4,5,6.
第一回合,庄家是玩家1,假设他选择了一张写着数字5的卡片。那么按顺时针数1,2,3,4,1,最后玩家1被踢出游戏。
第二回合,庄家就是玩家1的下一个人,即玩家2.假设玩家2这次选择了一张数字6,那么2,3,4,2,3,4,玩家4被踢出游戏。
第三回合,玩家2再一次成为庄家。如果这一次玩家2再次选了6,则玩家3被踢出游戏,最后的胜者就是玩家2.
输入格式:
第一行包括两个整数N,M分别表示玩家个数和卡牌总数。
接下来一行是包含M个整数,分别给出每张卡片上写的数字。
输出格式:
输出一行包含N个百分比形式给出的实数,四舍五入到两位小数。分别给出从玩家1到玩家N的胜出概率,每个概率之间用空格隔开,最后不要有空格。
输入样例#1:
5 5 2 3 5 7 11
输出样例#1:
22.72% 17.12% 15.36% 25.44% 19.36%
输入样例#2:
4 4 3 4 5 6
输出样例#2:
25.00% 25.00% 25.00% 25.00%
对于30%的数据,有1<=N<=10
对于50%的数据,有1<=N<=30
对于100%的数据,有1<=N<=50 1<=M<=50 1<=每张卡片上的数字<=50
10%自然就是爆搜乱搞了。50%实话说没想到。
看上去算法是[eq]O(n^3)[/eq]的。我们需要注意到一点,即淘汰的操作仅关心被淘汰人与庄家的相对位置关系,记录这个相对位置关系就好办了。且这个游戏每次只淘汰一人,即总是从剩i人向剩i-1人发展。设计状态dp[i][j]表示剩下i人从庄家开始顺时针数j人这个人胜出的概率,我们考虑随机从当前局面淘汰一人,只需要知道淘汰并且重新选定庄家后现在这个人在下一个局面的什么位置即可,即转移是
\displaystyle dp[i][j] = \sum \frac{dp[i-1][j']}{m}
还剩一人时这个人就胜出了,因此dp[1][1]=1。由于初始的时候1做庄家,答案就是dp[n][1]~dp[n][n]。
// Code by KSkun, 2018/4
#include <cstdio>
#include <cctype>
#include <cstring>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(!isdigit(c)) {
if(c == '-') neg = -1;
c = fgc();
}
while(isdigit(c)) {
res = (res << 1) + (res << 3) + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 55;
int n, m, a[MAXN];
double dp[MAXN][MAXN];
int main() {
n = readint(); m = readint();
for(int i = 1; i <= m; i++) {
a[i] = readint();
}
dp[1][1] = 1;
for(int i = 2; i <= n; i++) {
for(int j = 1; j <= i; j++) {
for(int k = 1; k <= m; k++) {
int nxt = a[k] % i;
if(!nxt) nxt = i;
if(nxt > j) dp[i][j] += dp[i - 1][i - nxt + j] / m;
else if(nxt < j) dp[i][j] += dp[i - 1][j - nxt] / m;
}
}
}
for(int i = 1; i <= n; i++) {
printf("%.2lf%% ", dp[n][i] * 100);
}
return 0;
}
965A Paper Airplanes 题意简述 一张纸可以做s个纸飞机,现在有k个人, …
题目地址:HDUOJ:Problem – 1695
Given 5 integers: a, b, c, d, k, you’re to find x in a…b, y in c…d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you’re only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.
Yoiu can assume that a = c = 1 in all test cases.
求[1, b]中的整数x与[1, d]中的整数y使得gcd(x, y)=k的数对(x, y)的数量。注意(5, 7)和(7, 5)只能算一对。
输入格式:
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.
输出格式:
For each test case, print the number of choices. Use the format in the example.
输入样例#1:
2 1 3 1 5 1 1 11014 1 14409 9
输出样例#1:
Case 1: 9 Case 2: 736427
本题需要的数学姿势:莫比乌斯反演原理及应用 | KSkun’s Blog
由于gcd(xk, yk)=k等价于gcd(x, y)=1,我们只需要求出[1, b/k]和[1, d/k]中互质的数对数即可。这样可以先行缩小b和d的范围。
我们构造函数f(n)为gcd(x, y)=n的数对数,而答案就是f(1)。这个函数求值很不好办,我们考虑构造另外一个函数F(n)为n|gcd(x, y)的数对数。我们先令p=b/k,q=d/k,很容易知道
F(n) = \frac{p}{n} \cdot \frac{q}{n}
然后研究f(n)和F(n)的关系,发现满足下面这个关系
F(n) = \sum_{n|d} f(d)
然后就可以用莫比乌斯反演
f(n) = \sum_{n|d} \mu(\frac{d}{n}) F(d)
由于我们求的是f(1),所以实际上是这样求的
f(1) = \sum_{i=1}^{\min(p, q)} \mu(i) \cdot \frac{p}{i} \cdot \frac{q}{i}
而由于题目要求去重,我们发现只有当x和y都处于 [1, \min(b, d)] 中时才会发生重复,因此我们令p=q=\min(b/k, d/k)再求一遍f(1),减去它的一半即可。
// Code by KSkun, 2018/4
#include <cstdio>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
register char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005;
bool notprime[MAXN];
int prime[MAXN], miu[MAXN], ptot;
inline void sieve() {
miu[1] = 1;
for(int i = 2; i <= MAXN; i++) {
if(!notprime[i]) {
prime[ptot++] = i;
miu[i] = -1;
}
for(int j = 0; j < ptot && prime[j] * i <= MAXN; j++) {
int k = prime[j] * i;
notprime[k] = true;
if(i % prime[j] == 0) {
miu[k] = 0; break;
} else {
miu[k] = -miu[i];
}
}
}
}
int T, a, b, c, d, k;
int main() {
sieve();
T = readint();
for(int kase = 1; kase <= T; kase++) {
LL all = 0, rep = 0;
a = readint(); b = readint(); c = readint(); d = readint(); k = readint();
if(!k) {
printf("Case %d: 0\n", kase);
continue;
}
b /= k; d /= k;
if(b > d) std::swap(b, d);
for(int i = 1; i <= b; i++) {
all += 1ll * miu[i] * (b / i) * (d / i);
}
for(int i = 1; i <= b; i++) {
rep += 1ll * miu[i] * (b / i) * (b / i);
}
printf("Case %d: %lld\n", kase, all - rep / 2);
}
return 0;
}