[HDU5181]numbers 题解
题目地址:HDUOJ:Problem – 5181 题目描述 Now you …
May all the beauty be blessed.
题目地址:BZOJ:Problem 2441. — [中山市选2011]小W的问题
有一天,小W找了一个笛卡尔坐标系,并在上面选取了N个整点。他发现通过这些整点能够画出很多个“W”出来。具体来说,对于五个不同的点(x1, y1), (x2, y2), (x3, y3), (x4, y4), (x5, y5),如果满足:
则称它们构成一个“W”形。
现在,小W想统计“W”形的个数,也就是满足上面条件的五元点组个数。你能帮助他吗?
输入格式:
第一行包含一个整数N,表示点的个数。
下面N行每行两个整数,第i+1行为(xi, yi),表示第i个点的坐标。
输出格式:
仅包含一行,为“W”形个数模1 000 000 007的值。
输入样例#1:
6 1 10 2 1 3 5 4 6 5 1 6 10
输出样例#1:
3
对于100%的数据满足N ≤ 200 000,0 ≤ xi ≤ 10^9,0 ≤ yi ≤ 10^9
首先我们考虑将一整个“W”拆成左右两个“V”形分别计算。我们以左高右低的“V”形为例。考虑一个点右上区域中的点数,这个点数可以认为是V形最左侧的可选点数。而对于一个V形右侧的点,能构成的V形数量显然就是左侧所有比它低的点的右上点之和。如果看到这里你还是感觉很懵,请看下面的图片。
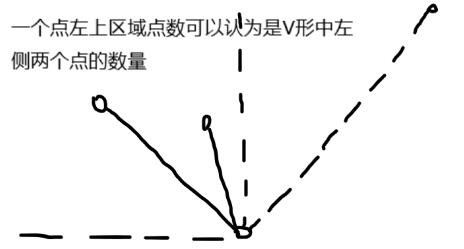
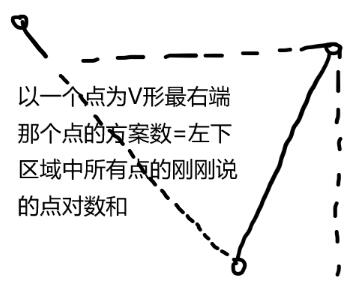
到这里,我们知道,我们要求的就是对于每个点,它左边任意一点的左上方的点的数量的和。我们先将点按y坐标排序,从小到大,每一次计算一层相同y坐标的点。我们用线段树维护x坐标(预先离散化)在这个区间内的点的左上方的点的数量的和。处理一个y坐标的时候,对于每一个点,把大于它x坐标的点的线段树区间-1,因为这个点已经低于之后处理的那些点了,无法成为V形左边的那个点。然后计算低于这个点的和,作为这个点能构成V形的数量。最后把这个点左边的点的个数加入线段树这个点x坐标的位置,和在这之前算过的-1合并作为这个点的左上点数量。需要注意的是,一层y坐标处理时,先对全部点处理-1,再对全部点计算答案,最后再对全部点计算左上点数量。这是因为同y坐标不能互为左上点,如果边计算答案边计算左上点数量,可能会算进去同y坐标的点的答案。
另一边左低右高的V形可以反着推一下,或者看代码的计算方法。
最后的答案为把同一个点两个V形的种类乘起来的和,原理是乘法原理。
这里我们需要对线段树进行魔改,因为有一些x坐标处没有点被计算过,这个位置的值还是负值,不应该加进去,所以要统计一下当前区间内有多少x坐标是算过的,维护一个len。细节看代码吧。
实话说,这个题属于“我知道我要求啥,但是我不知道怎么求要求的这个东西”的一类题目,看别人题解看的一脸懵逼,思路还是在写这篇文章的时候逐渐清晰的。考场上估计就是一脸不可做了。如果对过程还是很懵逼,在这篇文章下留言,我尽可能回答你的问题,并且改进题解叙述。
// Code by KSkun, 2018/3
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int readint() {
register int res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
// variables
const int MO = 1e9 + 7, MAXN = 200005, INF = 2e9;
int n;
LL f[MAXN][2], ans = 0;
struct Point {
int x, y, id, nx;
} pts[MAXN];
LL tmp[MAXN], ttot = 0;
inline bool cmpx(Point a, Point b) {
return a.x < b.x;
}
inline bool cmpy(Point a, Point b) {
return a.y < b.y;
}
// seg tree
struct Node {
LL val, add, len;
} tr[MAXN << 2];
inline void apply(int o, LL v) {
tr[o].add = (tr[o].add + v) % MO;
tr[o].val = (tr[o].val + v * tr[o].len) % MO;
}
inline void pushdown(int o, int l, int r) {
if(l == r) return;
int lch = o << 1, rch = o << 1 | 1;
if(tr[o].add != 0) {
apply(lch, tr[o].add);
apply(rch, tr[o].add);
tr[o].add = 0;
}
}
inline void merge(int o, int l, int r) {
if(l == r) return;
int lch = o << 1, rch = o << 1 | 1;
tr[o].val = 0;
tr[o].len = tr[lch].len + tr[rch].len;
if(tr[lch].len) tr[o].val = (tr[o].val + tr[lch].val) % MO;
if(tr[rch].len) tr[o].val = (tr[o].val + tr[rch].val) % MO;
}
inline void add(int o, int l, int r, int ll, int rr, LL v) {
if(ll > rr) return;
pushdown(o, l, r);
if(l >= ll && r <= rr) {
apply(o, v);
return;
}
int lch = o << 1, rch = o << 1 | 1, mid = (l + r) >> 1;
if(ll <= mid) add(lch, l, mid, ll, rr, v);
if(rr > mid) add(rch, mid + 1, r, ll, rr, v);
merge(o, l, r);
}
inline void add(int o, int l, int r, int x, LL v) {
pushdown(o, l, r);
if(l == r) {
tr[o].len = 1;
tr[o].val = (tr[o].add + v) % MO;
return;
}
int lch = o << 1, rch = o << 1 | 1, mid = (l + r) >> 1;
if(x <= mid) add(lch, l, mid, x, v);
if(x > mid) add(rch, mid + 1, r, x, v);
merge(o, l, r);
}
inline LL query(int o, int l, int r, int ll, int rr) {
if(ll > rr || !tr[o].len) return 0;
pushdown(o, l, r);
if(l >= ll && r <= rr) {
return tr[o].val;
}
int lch = o << 1, rch = o << 1 | 1, mid = (l + r) >> 1;
LL res = 0;
if(ll <= mid) res = (res + query(lch, l, mid, ll, rr)) % MO;
if(rr > mid) res = (res + query(rch, mid + 1, r, ll, rr)) % MO;
return res;
}
inline void add(int l, int r, LL v) {
add(1, 1, n, l, r, v);
}
inline void add(int x, LL v) {
add(1, 1, n, x, v);
}
inline LL query(int l, int r) {
return query(1, 1, n, l, r);
}
int main() {
n = readint();
for(int i = 1; i <= n; i++) {
pts[i].x = readint();
pts[i].y = readint();
tmp[++ttot] = pts[i].x;
}
tmp[++ttot] = INF;
std::sort(tmp + 1, tmp + ttot + 1);
std::sort(pts + 1, pts + n + 1, cmpx);
for(int i = 1; i <= n; i++) {
pts[i].nx = std::upper_bound(tmp + 1, tmp + ttot + 1, pts[i].x) - tmp;
pts[i].x = std::lower_bound(tmp + 1, tmp + ttot + 1, pts[i].x) - tmp;
pts[i].id = i;
}
std::sort(pts + 1, pts + n + 1, cmpy);
for(int i = 1; i <= n; i++) {
int j = i;
while(j < n && pts[i].y == pts[j + 1].y) j++;
for(int k = i; k <= j; k++) {
add(pts[k].nx, n, -1);
}
for(int k = i; k <= j; k++) {
f[pts[k].id][0] = query(1, pts[k].x - 1);
}
for(int k = i; k <= j; k++) {
add(pts[k].id, pts[k].x - 1);
}
i = j;
}
memset(tr, 0, sizeof(tr));
for(int i = 1; i <= n; i++) {
int j = i;
while(j < n && pts[i].y == pts[j + 1].y) j++;
for(int k = i; k <= j; k++) {
add(1, pts[k].x - 1, -1);
}
for(int k = i; k <= j; k++) {
f[pts[k].id][1] = query(pts[k].nx, n);
}
for(int k = i; k <= j; k++) {
add(pts[k].id, n - pts[k].nx + 1);
}
i = j;
}
for(int i = 1; i <= n; i++) {
ans = (ans + f[i][0] * f[i][1] % MO) % MO;
}
printf("%lld", ans);
return 0;
}
题目地址:洛谷:【P2042】[NOI2005]维护数列 – 洛谷、BZOJ:Problem 1500. — [NOI2005]维修数列
请写一个程序,要求维护一个数列,支持以下 6 种操作:(请注意,格式栏 中的下划线‘ _ ’表示实际输入文件中的空格)

输入格式:
输入文件的第 1 行包含两个数 N 和 M,N 表示初始时数列中数的个数,M 表示要进行的操作数目。 第 2 行包含 N 个数字,描述初始时的数列。 以下 M 行,每行一条命令,格式参见问题描述中的表格
输出格式:
对于输入数据中的 GET-SUM 和 MAX-SUM 操作,向输出文件依次打印结 果,每个答案(数字)占一行。
输入样例#1:
9 8 2 -6 3 5 1 -5 -3 6 3 GET-SUM 5 4 MAX-SUM INSERT 8 3 -5 7 2 DELETE 12 1 MAKE-SAME 3 3 2 REVERSE 3 6 GET-SUM 5 4 MAX-SUM
输出样例#1:
-1 10 1 10
你可以认为在任何时刻,数列中至少有 1 个数。
输入数据一定是正确的,即指定位置的数在数列中一定存在。
50%的数据中,任何时刻数列中最多含有 30 000 个数;
100%的数据中,任何时刻数列中最多含有 500 000 个数。
100%的数据中,任何时刻数列中任何一个数字均在[-1 000, 1 000]内。
100%的数据中,M ≤20 000,插入的数字总数不超过 4 000 000 。
样例说明:

这个题是Splay模板之集大全者哇,A掉了Splay的常见用法基本就见过了。
我们分开说这些操作吧。
这些操作都可以用split-perform这种模式去写。
以插入为例,首先对插入的内容现场建成splay,然后把x-1位置splay到根,x+tot位置splay到根的右儿子。在x+tot位置的左儿子处把新的splay挂上去就行。split操作就是上面的两次splay。
具体的实现可以参考代码。
可以维护四个量,区间和、区间最大子列,区间以左侧为起点的最大子列,区间以右侧为起点的最大子列。操作后动态更新这些量,询问的时候先split再查即可。
更新的方法如下。
区间最大子列:max(左儿子右侧最大子列+中间值+右儿子左侧最大子列,左右儿子的最大子列)
区间左侧最大子列:max(左儿子和+中间值+右儿子左侧最大子列,左儿子左侧最大子列)
右侧类似。
其他细节看代码吧。
// Code by KSkun, 2018/3
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while (c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline int readstr(char str[], int startpos) {
char c = '*';
int siz = startpos;
while((c < 'A' || c > 'Z') && c != '-') c = fgc();
while((c >= 'A' && c <= 'Z') || c == '-') {
str[siz++] = c;
c = fgc();
}
str[siz] = '\0';
return siz - startpos;
}
inline int readop() {
char ops[20];
readstr(ops, 0);
if(ops[2] == 'S') return 1;
if(ops[2] == 'L') return 2;
if(ops[2] == 'K') return 3;
if(ops[2] == 'V') return 4;
if(ops[2] == 'T') return 5;
if(ops[2] == 'X') return 6;
return 0;
}
// variables
const int MAXN = 500005, MAXI = 4000005, INF = 1e9;
int n, m, op, xt, lent;
LL ct, a[MAXI];
// splay
struct Node {
LL val, mxs, mxl, mxr, sum;
bool rev, rep;
int ch[2], siz, fa;
} tr[MAXN];
int tot = 0, sta[MAXN], stop = 0, rt = 0;
inline void update(int p) {
int lch = tr[p].ch[0], rch = tr[p].ch[1];
tr[p].siz = tr[lch].siz + tr[rch].siz + 1;
tr[p].sum = tr[lch].sum + tr[rch].sum + tr[p].val;
tr[p].mxs = std::max(tr[lch].mxr + tr[p].val + tr[rch].mxl, std::max(tr[lch].mxs, tr[rch].mxs));
tr[p].mxl = std::max(tr[lch].mxl, tr[lch].sum + tr[p].val + tr[rch].mxl);
tr[p].mxr = std::max(tr[rch].mxr, tr[rch].sum + tr[p].val + tr[lch].mxr);
}
inline void pushdown(int p) {
int lch = tr[p].ch[0], rch = tr[p].ch[1];
if(tr[p].rep) {
if(lch) {
tr[lch].rep = true;
tr[lch].val = tr[p].val;
tr[lch].sum = tr[p].val * tr[lch].siz;
if(tr[p].val >= 0) {
tr[lch].mxl = tr[lch].mxr = tr[lch].mxs = tr[lch].sum;
} else {
tr[lch].mxl = tr[lch].mxr = 0;
tr[lch].mxs = tr[p].val;
}
}
if(rch) {
tr[rch].rep = true;
tr[rch].val = tr[p].val;
tr[rch].sum = tr[p].val * tr[rch].siz;
if(tr[p].val >= 0) {
tr[rch].mxl = tr[rch].mxr = tr[rch].mxs = tr[rch].sum;
} else {
tr[rch].mxl = tr[rch].mxr = 0;
tr[rch].mxs = tr[p].val;
}
}
tr[p].rep = tr[p].rev = false;
}
if(tr[p].rev) {
std::swap(tr[lch].mxl, tr[lch].mxr);
std::swap(tr[lch].ch[0], tr[lch].ch[1]);
std::swap(tr[rch].mxl, tr[rch].mxr);
std::swap(tr[rch].ch[0], tr[rch].ch[1]);
tr[lch].rev = !tr[lch].rev;
tr[rch].rev = !tr[rch].rev;
tr[p].rev = false;
}
}
inline int newnode() {
int p;
if(stop > 0) {
p = sta[--stop];
} else {
p = ++tot;
}
memset(tr + p, 0, sizeof(Node));
return p;
}
inline void delnode(int a) {
sta[stop++] = a;
}
inline bool isleft(int p) {
return tr[tr[p].fa].ch[0] == p;
}
inline void rotate(int p) { // p is child
bool type = !isleft(p);
int fa = tr[p].fa, ffa = tr[fa].fa;
tr[fa].ch[type] = tr[p].ch[!type];
tr[p].ch[!type] = fa;
tr[tr[fa].ch[type]].fa = fa;
if(ffa) tr[ffa].ch[!isleft(fa)] = p;
tr[p].fa = tr[fa].fa;
tr[fa].fa = p;
update(fa);
update(p);
}
inline void splay(int p, int tar) {
for(int fa; (fa = tr[p].fa) != tar; rotate(p)) {
if(tr[tr[p].fa].fa != tar) {
rotate(isleft(fa) == isleft(p) ? fa : p);
}
}
if(!tar) rt = p;
}
inline int find(int p, int rk) {
pushdown(p);
int lch = tr[p].ch[0], rch = tr[p].ch[1];
if(tr[lch].siz + 1 == rk) return p;
else if(tr[lch].siz >= rk) return find(lch, rk);
else return find(rch, rk - tr[lch].siz - 1);
}
inline int build(int fa, int l, int r) {
if(l > r) return 0;
int p = newnode();
if(l == r) {
tr[p].siz = 1;
tr[p].val = tr[p].sum = tr[p].mxs = a[l];
tr[p].mxl = tr[p].mxr = a[l] >= 0 ? a[l] : 0;
tr[p].fa = fa;
return p;
}
int mid = (l + r) >> 1;
tr[p].ch[0] = build(p, l, mid - 1);
tr[p].ch[1] = build(p, mid + 1, r);
tr[p].fa = fa;
tr[p].val = a[mid];
update(p);
return p;
}
inline void insert(int x, int len) {
for(int i = 1; i <= len; i++) {
a[i] = readint();
}
int p = build(0, 1, len), a = find(rt, x + 1), b = find(rt, x + 2);
splay(a, 0);
splay(b, a);
tr[p].fa = b;
tr[b].ch[0] = p;
update(b);
update(a);
}
inline void eraset(int p) {
if(!p) return;
delnode(p);
eraset(tr[p].ch[0]);
eraset(tr[p].ch[1]);
}
inline void erase(int x, int len) {
int a = find(rt, x), b = find(rt, x + len + 1);
splay(a, 0);
splay(b, a);
eraset(tr[b].ch[0]);
tr[b].ch[0] = 0;
update(b);
update(a);
}
inline void replace(int x, int len, LL val) {
int a = find(rt, x), b = find(rt, x + len + 1);
splay(a, 0);
splay(b, a);
int p = tr[b].ch[0];
tr[p].val = val;
tr[p].rep = true;
tr[p].sum = val * tr[p].siz;
if(val >= 0) {
tr[p].mxl = tr[p].mxr = tr[p].mxs = tr[p].sum;
} else {
tr[p].mxl = tr[p].mxr = 0;
tr[p].mxs = val;
}
update(b);
update(a);
}
inline void reverse(int x, int len) {
int a = find(rt, x), b = find(rt, x + len + 1);
splay(a, 0);
splay(b, a);
int p = tr[b].ch[0];
if(!tr[p].rep) {
tr[p].rev = !tr[p].rev;
std::swap(tr[p].mxl, tr[p].mxr);
std::swap(tr[p].ch[0], tr[p].ch[1]);
update(b);
update(a);
}
}
inline LL querysum(int x, int len) {
int a = find(rt, x), b = find(rt, x + len + 1);
splay(a, 0);
splay(b, a);
int p = tr[b].ch[0];
return tr[p].sum;
}
inline LL querymxs() {
int a = find(rt, 1), b = find(rt, n);
splay(a, 0);
splay(b, a);
int p = tr[b].ch[0];
return tr[p].mxs;
}
int main() {
n = readint();
m = readint();
tr[0].mxs = a[1] = a[n + 2] = -INF;
for(int i = 1; i <= n; i++) {
a[i + 1] = readint();
}
rt = build(0, 1, n + 2);
n += 2;
while(m--) {
op = readop();
if(op != 6) {
xt = readint();
lent = readint();
}
if(op == 1) {
insert(xt, lent);
n += lent;
}
if(op == 2) {
erase(xt, lent);
n -= lent;
}
if(op == 3) {
ct = readint();
replace(xt, lent, ct);
}
if(op == 4) {
reverse(xt, lent);
}
if(op == 5) {
printf("%lld\n", querysum(xt, lent));
}
if(op == 6) {
printf("%lld\n", querymxs());
}
}
return 0;
}