Splay原理与实现
注:本文部分图片来自互联网,其相关权利归原作者所有,感谢原作者的分享。 概述 Splay( …
May all the beauty be blessed.
题目地址:洛谷:【SP10628】COT – Count on a tree – 洛谷、SPOJ:SPOJ.com – Problem COT、BZOJ:Problem 2588. — Spoj 10628. Count on a tree
You are given a tree with N nodes. The tree nodes are numbered from 1 to N. Each node has an integer weight.
We will ask you to perform the following operation:
u v k : ask for the kth minimum weight on the path from node u to node v给你一棵带点权的树,每次询问求u到v路径上的k小权值。
输入格式:
In the first line there are two integers N and M. (N, M <= 100000)
In the second line there are N integers. The ith integer denotes the weight of the ith node.
In the next N-1 lines, each line contains two integers u v, which describes an edge (u, v).
In the next M lines, each line contains three integers u v k, which means an operation asking for the kth minimum weight on the path from node u to node v.
输出格式:
For each operation, print its result.
输入样例#1:
8 5 105 2 9 3 8 5 7 7 1 2 1 3 1 4 3 5 3 6 3 7 4 8 2 5 1 2 5 2 2 5 3 2 5 4 7 8 2
输出样例#1:
2 8 9 105 7
这是一个主席树的题目。考虑每个点建一个权值线段树,维护从根到该点的路径权值。DFS一遍,对于一个点,从其父亲处插入该点的权值。权值需要离散化处理一下。直接钦点1为树根也行。询问的时候,查询该点LCA,查询时路径上的答案为u+v-lca-fa[lca],考虑像区间k小值那样,四个线段树一起跑。这里我的LCA是倍增写法。
// Code by KSkun, 2018/2
#include <cstdio>
#include <cmath>
#include <vector>
#include <algorithm>
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int readint() {
register int res = 0, neg = 1;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while (c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005;
int n, m, w[MAXN], ut, vt, kt;
std::vector<int> gra[MAXN];
int tmp[MAXN], tsiz;
// seg tree
struct Node {
int lch, rch, val;
} tree[MAXN << 5];
int tot = 0, rt[MAXN];
inline void insert(int &o, int l, int r, int x) {
tree[++tot] = tree[o];
o = tot;
tree[o].val++;
if(l == r) return;
int mid = (l + r) >> 1;
if(x <= mid) insert(tree[o].lch, l, mid, x);
else insert(tree[o].rch, mid + 1, r, x);
}
inline int query(int lo, int ro, int fo, int ffo, int l, int r, int k) {
if(l == r) return l;
int mid = (l + r) >> 1;
int num = tree[tree[lo].lch].val + tree[tree[ro].lch].val - tree[tree[fo].lch].val - tree[tree[ffo].lch].val;
if(k <= num) return query(tree[lo].lch, tree[ro].lch, tree[fo].lch, tree[ffo].lch, l, mid, k);
else return query(tree[lo].rch, tree[ro].rch, tree[fo].rch, tree[ffo].rch, mid + 1, r, k - num);
}
// lca
int l2n, dep[MAXN], anc[MAXN][20];
void dfs(int u) {
rt[u] = rt[anc[u][0]];
insert(rt[u], 1, tsiz, w[u]);
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(v == anc[u][0]) {
continue;
}
dep[v] = dep[u] + 1;
anc[v][0] = u;
dfs(v);
}
}
inline void init() {
for(int j = 1; (1 << j) <= n; j++) {
for(int i = 1; i <= n; i++) {
anc[i][j] = anc[anc[i][j - 1]][j - 1];
}
}
}
inline int lca(int a, int b) {
if(dep[a] > dep[b]) std::swap(a, b);
int del = dep[b] - dep[a];
for(int i = 0; (1 << i) <= del; i++) {
if((1 << i) & del) b = anc[b][i];
}
if(a != b) {
for(int i = l2n; i >= 0; i--) {
if(anc[a][i] != anc[b][i]) {
a = anc[a][i];
b = anc[b][i];
}
}
return anc[a][0];
} else {
return a;
}
}
int main() {
n = readint();
m = readint();
l2n = log(n) / log(2);
for(int i = 1; i <= n; i++) {
tmp[i] = w[i] = readint();
}
std::sort(tmp + 1, tmp + n + 1);
tsiz = std::unique(tmp + 1, tmp + n + 1) - tmp - 1;
for(int i = 1; i <= n; i++) {
w[i] = std::lower_bound(tmp + 1, tmp + tsiz + 1, w[i]) - tmp;
}
for(int i = 1; i <= n - 1; i++) {
ut = readint();
vt = readint();
gra[ut].push_back(vt);
gra[vt].push_back(ut);
}
dfs(1);
init();
while(m--) {
ut = readint();
vt = readint();
kt = readint();
int lcat = lca(ut, vt);
printf("%d\n", tmp[query(rt[ut], rt[vt], rt[lcat], rt[anc[lcat][0]], 1, tsiz, kt)]);
}
return 0;
}
题目地址:洛谷:、BZOJ:Problem 1568. — [JSOI2008]Blue Mary开公司
Blue Mary 最近在筹备开一家自己的网络公司。由于他缺乏经济头脑,所以先后聘请了若干个金融顾问为他设计经营方案。
万事开头难,经营公司更是如此。开始的收益往往是很低的,不过随着时间的增长会慢慢变好。也就是说,对于一个金融顾问 i,他设计的经营方案中,每天的收益都比前一天高,并且均增长一个相同的量 Pi。
由于金融顾问的工作效率不高,所以在特定的时间,Blue Mary 只能根据他已经得到的经营方案来估算某一时间的最大收益。由于 Blue Mary 是很没有经济头脑的,所以他在估算每天的最佳获益时完全不会考虑之前的情况,而是直接从所有金融顾问的方案中选择一个在当天获益最大的方案的当天的获益值,例如:
有如下两个金融顾问分别对前四天的收益方案做了设计:
| 第一天 | 第二天 | 第三天 | 第四天 | Pi | |
|---|---|---|---|---|---|
| 顾问 1 | 1 | 5 | 9 | 13 | 4 |
| 顾问 2 | 2 | 5 | 8 | 11 | 3 |
在第一天,Blue Mary认为最大收益是 2(使用顾问 2 的方案),而在第三天和第四天,他认为最大收益分别是 9 和 13(使用顾问 1 的方案)。而他认为前四天的最大收益是:
2 + 5 + 9 + 13 = 29
现在你作为 Blue Mary 公司的副总经理,会不时收到金融顾问的设计方案,也需要随时回答 Blue Mary 对某天的“最大收益”的询问(这里的“最大收益”是按照 Blue Mary 的计算方法)。一开始没有收到任何方案时,你可以认为每天的最大收益值是 0。下面是一组收到方案和回答询问的例子:
询问 2 回答 0 收到方案:0 1 2 3 4 5 …… 询问 2 回答 1 收到方案:2 2.1 2.2 2.3 2.4 …… 询问 2 回答 2.1
输入格式:
第一行 :一个整数 N,表示方案和询问的总数。
接下来 N 行,每行开头一个单词Query或Project。
若单词为Query,则后接一个整数 T,表示 Blue Mary 询问第 T 天的最大收益。
若单词为Project,则后接两个实数 S,P,表示该种设计方案第一天的收益 S,以及以后每天比上一天多出的收益 P。
输出格式:
对于每一个Query,输出一个整数,表示询问的答案,并精确到整百元(以百元为单位,例如:该天最大收益为 210 或 290 时,均应该输出 2)。没有方案时回答询问要输出 0。
吐槽:这个样例给了跟没给有啥区别?
输入样例#1:
10 Project 5.10200 0.65000 Project 2.76200 1.43000 Query 4 Query 2 Project 3.80200 1.17000 Query 2 Query 3 Query 1 Project 4.58200 0.91000 Project 5.36200 0.39000
输出样例#1:
0 0 0 0 0
数据范围:
1 \leq N \leq 100000, 1 \leq T \leq 50000, 0 < P < 100, |S| \leq 10^5
提示:
本题读写数据量可能相当巨大,请选手注意选择高效的文件读写方式。
这个要用到线段树的标记永久化用法。
标记永久化是指一个标记打到区间上以后,不再下放(即pushdown),而是由查询的时候向上查询标记并更新答案。
这里相当于加入若干直线,并且询问x坐标固定时y坐标最大的值。我们考虑让线段树中存下这些直线在每个区间对应的中点值最大的线段(这里的线段是抽象说法,而非实现写法)。对于插入一根直线,我们考虑这根直线跟现在已有的直线的关系。如下图,共有4种情况:
黑色为已有直线,蓝色为待加入直线。
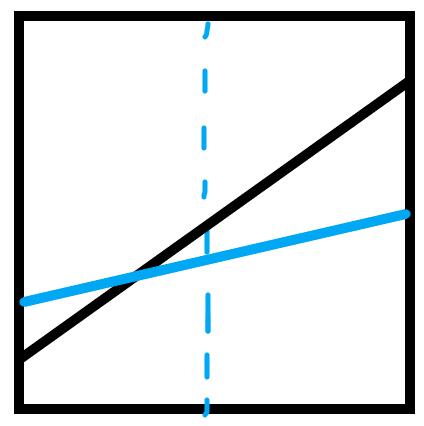
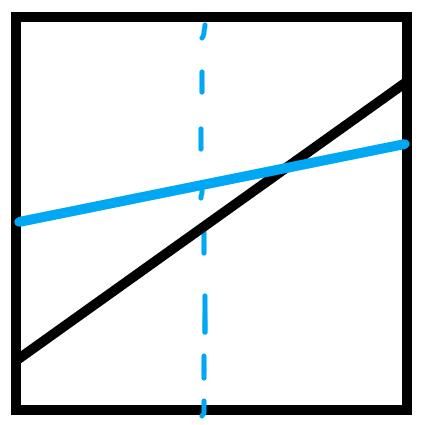
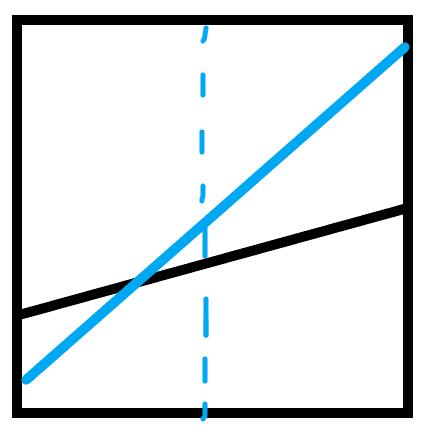
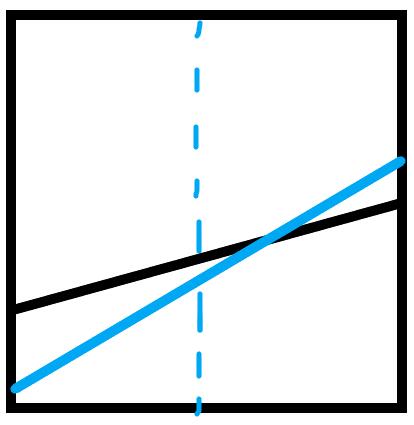
对于每种情况,我们把中点值大的直线存在这个区间,并且把有交点的那一半区间递归下去处理。
查询时,从该点往上找,更新区间存的直线该点的函数值。
// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while (c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline double readdemi() {
register double res = 0;
register int siz = 0, neg = 1;
register bool indem = false;
char c = fgc();
while (c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while ((c >= '0' && c <= '9') || c == '.') {
if(c == '.') {
indem = true;
c = fgc();
continue;
}
if(indem) siz++;
res = res * 10 + c - '0';
c = fgc();
}
while(siz--) res /= 10;
return res * neg;
}
const int MAXN = 50005, N = 50000, MAXM = 100005;
inline bool isop(char c) {
return c == 'P' || c == 'Q';
}
inline char readop() {
char c = fgc();
while (!isop(c)) c = fgc();
return c;
}
int q, t;
char op;
double s[MAXM], p[MAXM];
int ptot = 1;
inline double cal(int line, int x) {
return s[line] + (x - 1) * p[line];
}
inline bool cmp(int l1, int l2, int x) { // if l1 bigger than l2 on pos x
return cal(l1, x) > cal(l2, x);
}
#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)
int tree[MAXN << 2];
inline void modify(int o, int l, int r, int line) {
if(l == r) {
if(cmp(line, tree[o], l)) tree[o] = line;
return;
}
if(p[line] > p[tree[o]]) {
if(cmp(line, tree[o], mid)) {
modify(lch, l, mid, tree[o]);
tree[o] = line;
} else {
modify(rch, mid + 1, r, line);
}
} else {
if(cmp(line, tree[o], mid)) {
modify(rch, mid + 1, r, tree[o]);
tree[o] = line;
} else {
modify(lch, l, mid, line);
}
}
}
inline double query(int o, int l, int r, int x) {
double res = cal(tree[o], x);
if(l == r) {
return res;
}
if(x <= mid) res = std::max(res, query(lch, l, mid, x));
if(x > mid) res = std::max(res, query(rch, mid + 1, r, x));
return res;
}
int main() {
q = readint();
while(q--) {
op = readop();
if(op == 'P') {
s[ptot] = readdemi();
p[ptot] = readdemi();
modify(1, 1, N, ptot);
ptot++;
}
if(op == 'Q') {
t = readint();
printf("%.0lf\n", floor(query(1, 1, N, t) / 100));
}
}
return 0;
}
题目地址:洛谷:【P4243】[JSOI2009]等差数列 – 洛谷、BZOJ:Problem 1558. — [JSOI2009]等差数列
“一个长度为l的数列ai,若相邻两数间的差a_i - a_{i-1} \ (2 \leq i \leq l)全部相同,则这个数列为等差数列。”火星特级数学老师jyy,正在给他的火星学生们上数学课。
为了检验学生的掌握情况,jyy布置了一道习题:给定一个长度为N (1≤N≤100,000)的数列,初始时第i个数为vi(vi是整数,−100,000≤vi≤100,000),学生们要按照jyy的给出的操作步骤来改变数列中的某些项的值。操作步骤的具体形式为:A s t a b (s, t, a, b均为整数,1≤s≤t≤N,−100,000≤a,b≤100,000),它表示,在序列的[s, t]区间上加上初值为a,步长为b的等差数列。即vi变为v_i + a + b \times (i - s)(对于s≤i≤t)。
在焦头烂额地计算之余,可怜的火星学生们还得随时回答jyy提出的问题。问题形式为:B s t(s, t均为整数,1≤s≤t≤N),表示jyy询问当前序列的[s, t]区间最少能划分成几段,使得每一段都是等差数列。比如说1 2 3 5 7最少能划分成2段,一段是1 2 3,另一段是5 7。询问是需要同学们计算出答案后,作为作业交上来的。
虽然操作数加问题数总共只有Q(1≤Q≤100,000)个,jyy还是觉得这个题很无聊很麻烦。于是他想让你帮他算一份标准答案。
输入格式:
第1行:1个整数N,第2…N+1行:每行一个整数。第i+1行表示vi。
第N+2行:1个整数Q,第N+3…N+Q+2行:每行描述了一个操作或问题,格式如题中所述,不含引号。
输出格式:
若干行,每行一个整数,表示对一个问题的回答。请按照输入中的顺序依次给出回答。
输入样例#1:
5 1 3 -1 -4 7 2 A 2 4 -1 5 B 1 5
输出样例#1:
2
样例说明:
原数列1 3 -1 -4 7。经过操作之后,数列变为1 2 3 5 7。如题中所述,最少能划分成2段。
数据规模:
对30%的数据,N,Q≤5000。
对100%的数据,1≤N,Q≤100,000。
其他数据范围见题面。
本题题解思路来自bzoj1558 [JSOI2009]等差数列 – zbtrs – 博客园,感谢原作者。
看到维护等差数列,我们想到维护这个数列的差分数列。
差分数列是啥呀?简单来说就是把数列的每项换成相邻两项的差值,也就是说,b_i = a_{i+1} - a_i。等差数列在差分数列中的表现就是连续一段相同值,这个值就是等差数列的公差(或者叫步长)。
让我们探索一下在差分数列上加等差数列操作应该怎么做。可以发现这个操作只影响首项和前一项(l-1)、末项和后一项(r)的值。用线段树维护这个序列就是两个单点加加一个区间加公差。
假如我们已经有了一个差分数列,连续的相同数字这一段就是一个等差数列,那么零散的不连续值呢?
让我们举个例子:
1 2 3 (4 4 4) 1 2 (3 3) 1 2差分数列
1 2 4 (7 11 15 19) 20 (22 25 28) 29 31原数列
显然原数列中那些属于零散值的数字可以成对构成等差数列。也就是说,连续一段零散值能构成的等差数列数量应该是这一段的长度/2。
接下来是一个问题:差分数列上一段数对应原数列中的长度应该+1,为什么直接/2是正确的呢?当我们求数列中间的一段零散值,实际上左右两边都是等差数列。如果使左右两边等差数列的长度最大,实际上原数列中零散的数量应该是-1的,因为左右端点被包含进左右的等差数列了。如果是左右端的零散值,则有一端无法包含进等差数列,原数列对应的长度即为差分数列零散值的长度。
这一段是很多博主并没有注明的细节,我在理解中也遇到了困惑,在这里特别讲解了一下。
为什么我们需要知道以上内容呢?因为维护左右两端的零散值数量方便区间的合并,而区间合并是线段树的基本操作。
记下这个区间左右两端的零散值长度、左右两端点值(合并区间时检查左儿子的右端和右儿子的左端是否值相等,即并成一个等差数列)、除了零散值以外的那一段能够划分成最少多少等差数列、区间长度。另外区间加操作的lazy标记在这里也是可以用的。
从长度为1的区间开始设置初值即可。
不可避免地,这题会遇到分类讨论。下面让我们慢慢地整理一下。
默认:本区间划分数为左右儿子划分数之和。
1.左右儿子都是纯零散值
需要检查左儿子的右端点和右儿子的左端点是否相等。(以下省略这句话)
相等→中间构成长为2的等差数列,左端零散值长为左儿子-1,右端零散值长为右儿子-1,本区间内除两端零散值以外的部分的划分数(以下简称划分数)为1。
不相等→左右两端零散值长都为本区间长,划分数为0。
2.左儿子是纯零散值,右儿子不是
本区间右端零散值长为右儿子右端零散值长。
相等→中间构成长为2的等差数列,左端零散值长为左儿子-1,将右儿子左端零散值构成的等差数列数加入划分数。
不相等→将左儿子和右儿子左端零散值合并作为本区间左端零散值。
3.右儿子是纯零散值,左儿子不是
从2情况翻转一下即可。自己推一下吧。
以下情况即可认为:本区间左端零散值长等于左儿子左端零散值长,右端同理。
4.左儿子右端和右儿子左端无零散值
相等→划分数要-1,除去重复计算的跨左右儿子的等差数列。
不相等→算到当前步骤的结果就是本区间结果。
5.左儿子右端无零散值,右儿子左端有零散值
不相等→将右儿子左端零散值构成的等差数列数加入划分数。
相等→加入后-1,理由同上。
6.右儿子左端无零散值,左儿子右端有零散值
从5情况翻转一下即可。自己推一下吧。
7.除上的一般情况
不相等→将左儿子右端和右儿子左端零散值构成的等差数列数加入划分数。
相等→左儿子右端和右儿子左端零散值数先都-1再计算构成等差数列数,加入划分数后加1,为了特殊处理跨左右儿子的等差数列。
到此所有的情况都讨论完成了。把这些情况写全了就不会出事。
这个题是个线段树直接维护答案的题,关键点在差分数列和区间合并的讨论。细节处理很要命,考场上要冷静分析,讨论全面。我反正是写不出的(笑)。
其他细节参考一下底下的代码吧,自认为代码风格还是很整洁的。没有注释可能看起来比较费劲。可以尝试对应着上面的解析看。
注:区间信息中,l、r是左右端点值,llen、rlen是左右端零散值长,ans是划分数,tag是lazy标记,siz是区间长。
// Code by KSkun, 2018/2
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 100005;
LL n, q, s, t, a, b;
char op;
inline bool isop(char c) {
return c == 'A' || c == 'B';
}
inline char readop() {
char c = fgc();
while(!isop(c)) c = fgc();
return c;
}
#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)
struct Data {
LL l, r, llen, rlen, ans, tag, siz;
} tree[MAXN << 2];
LL val[MAXN];
inline void pushdown(int o) {
if(tree[o].tag) {
tree[lch].tag += tree[o].tag;
tree[lch].l += tree[o].tag;
tree[lch].r += tree[o].tag;
tree[rch].tag += tree[o].tag;
tree[rch].l += tree[o].tag;
tree[rch].r += tree[o].tag;
tree[o].tag = 0;
}
}
inline void merge(Data *dest, Data lson, Data rson) {
Data *rt = dest, *ls = &lson, *rs = &rson;
bool flag = ls->r == rs->l;
memset(rt, 0, sizeof(Data));
rt->siz = ls->siz + rs->siz;
rt->l = ls->l;
rt->r = rs->r;
rt->ans = ls->ans + rs->ans;
if(ls->ans == 0 && rs->ans == 0) {
if(flag) {
rt->llen = ls->llen - 1;
rt->rlen = rs->rlen - 1;
rt->ans++;
} else {
rt->llen = rt->rlen = rt->siz;
}
return;
}
if(ls->ans == 0) {
rt->rlen = rs->rlen;
if(flag) {
rt->llen = ls->llen - 1;
if(rs->llen) {
rt->ans += (rs->llen - 1) / 2 + 1;
}
} else {
rt->llen = ls->siz + rs->llen;
}
return;
}
if(rs->ans == 0) {
rt->llen = ls->llen;
if(flag) {
rt->rlen = rs->rlen - 1;
if(ls->rlen) {
rt->ans += (ls->rlen - 1) / 2 + 1;
}
} else {
rt->rlen = rs->siz + ls->rlen;
}
return;
}
rt->llen = ls->llen;
rt->rlen = rs->rlen;
if(ls->rlen == 0 && rs->llen == 0) {
if(flag) {
rt->ans--;
}
return;
}
if(ls->rlen == 0) {
if(flag) {
rt->ans += (rs->llen - 1) / 2;
} else {
rt->ans += rs->llen / 2;
}
return;
}
if(rs->llen == 0) {
if(flag) {
rt->ans += (ls->rlen - 1) / 2
} else {
rt->ans += ls->rlen / 2;
}
return;
}
LL toadd = (ls->rlen + rs->llen) / 2;
if(flag) {
toadd = std::min(toadd, (ls->rlen - 1) / 2 + (rs->llen - 1) / 2 + 1);
}
rt->ans += toadd;
}
inline void build(int o, int l, int r) {
if(l == r) {
tree[o].l = tree[o].r = val[l];
tree[o].llen = tree[o].rlen = tree[o].siz = 1;
return;
}
build(lch, l, mid);
build(rch, mid + 1, r);
merge(&tree[o], tree[lch], tree[rch]);
}
inline void add(int o, int l, int r, int ll, int rr, LL v) {
if(l >= ll && r <= rr) {
tree[o].l += v;
tree[o].r += v;
tree[o].tag += v;
return;
}
pushdown(o);
if(mid >= ll) {
add(lch, l, mid, ll, rr, v);
}
if(mid < rr) {
add(rch, mid + 1, r, ll, rr, v);
}
merge(&tree[o], tree[lch], tree[rch]);
}
inline Data query(int o, int l, int r, int ll, int rr) {
if(l >= ll && r <= rr) {
return tree[o];
}
pushdown(o);
if(rr <= mid) {
return query(lch, l, mid, ll, rr);
} else if(ll > mid) {
return query(rch, mid + 1, r, ll, rr);
} else {
Data res;
merge(&res, query(lch, l, mid, ll, mid), query(rch, mid + 1, r, mid + 1, rr));
return res;
}
}
int main() {
n = readint();
for(int i = 1; i <= n; i++) {
val[i] = readint();
}
for(int i = 1; i <= n - 1; i++) {
val[i] = val[i + 1] - val[i];
}
n--;
build(1, 1, n);
q = readint();
while(q--) {
op = readop();
if(op == 'A') {
s = readint();
t = readint();
a = readint();
b = readint();
if(s > 1) {
add(1, 1, n, s - 1, s - 1, a);
}
if(t <= n) {
add(1, 1, n, t, t, -(a + (t - s) * b));
}
if(s < t) {
add(1, 1, n, s, t - 1, b);
}
}
if(op == 'B') {
s = readint();
t = readint();
if(s == t) {
printf("1\n");
continue;
}
Data res = query(1, 1, n, s, t - 1);
LL ans = (t - s + 2) / 2;
if(res.ans == 0) {
printf("%lld\n", ans);
} else {
ans = std::min(ans, res.ans + (res.llen + 1) / 2 + (res.rlen + 1) / 2);
printf("%lld\n", ans);
}
}
}
return 0;
}