[工程师死绝的世界D4003]アンドロイドの生産工場 翻译及题解
机器人生产工厂 Translation by KSkun 原题:問題「アンドロイドの生産工 …
May all the beauty be blessed.
Translation by KSkun
原题:問題「荒れ果てた警察署」 | エンジニアが死滅シタ世界 〜アンドロイドとふたりぼっちで生きろ〜
警察局的门有一个密码锁,密码由3位从0到9的数字构成,如果输入正确,锁就会打开。
你已经知道了密码的前两位,而第三位是由以下的规则来决定的:
你已经知道了前两位数字,所以请你计算出密码的第三位。
n_1 n_2
请根据以下规则计算密码的第三位数字。
在输出的末尾输出一个换行符,不应包含其他字符或空行。
输入:
4 8
输出:
2
输入:
9 1
输出:
0
// Code by KSkun, 2019/1
#include <cstdio>
#include <cctype>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
LL res = 0, neg = 1; char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
inline char readsingle() {
char c;
while(!isgraph(c = fgc())) {}
return c;
}
int n1, n2;
int main() {
n1 = readint(); n2 = readint();
printf("%d\n", (n1 + n2) % 10);
return 0;
}
配合音乐食用体验更佳
之前出过一档子事,有个朋友深夜特别容易焦虑,当时有一句话说的特别好:晚上就应该去睡觉,不要让胡思乱想扰了心。我也是个喜欢胡思乱想的人,晚上洗澡睡前这些个时候日常talking nonsense。
想来想去,觉得这些个想法也挺有意思的,就记录下来吧。这才有了这档子《胡思乱想》杂谈。今天离2019高考还有98天,怕不是踏了《高考恋爱100天》高考胡扯100天的路子。本栏目不定期更新,不欢迎大家关注。
本期主题:悲凉凄惨的人生(至今为止)
作为退役选手了,还经常关注OI方面的事情,甚至比现役选手还操心些,活的一点不像一个退役专心高三的人呢。
回想自己OI的历史,是真的非常不专业。去年1月去清北学堂的省选特训,半个字没听懂,群倒是水了一大堆,甚至还捡起了MC Modding,加入了他们晚自习游戏制作大军的行列。还就是这时候让我真实地感受到了在NOIP以后水到底有多深,做了停课的决心,苦苦啃培训的课件之类。
3个月后,省选Day 2爆零,成功垫底。同月APIO,比较拿手的树DP没grab住,打了个铜。狠狠心停到NOI,2w2买D,由于SAM太菜以及exCRT忘板子再次垫底。这些经历相比那些在考场现推各种数学原理不需要背板的头铁选手来说,无一不体现我学的知识是有多浅,很大一部分根本没有理解透彻就被拿来使用,结果就是浮于表面,没有什么大作用。
再说久一些吧,小学考本县最好私立,虽然被当时培训班的老师说有天赋,全免生依然还是无缘了。从广东回十堰读初中,入学考的很普通,逐渐变优秀了以后居然还出了一次排名断崖式下跌的岔子。考华一专县生,依然是知识学的不够精,连国际部都去不了。厚着脸皮call几次招生老师,肯定是没用的啦。高中来了郧中,好好的胚子被竞赛断送了(班主任观点)。
没有大成功过的我,现在在这个博雅班(火箭班)上,是很黯淡无光了。一次清华的招生座谈,话题是对清华的印象,理科这边有去过清华工科营的dalao分享现场激烈状况,文科有dalao发表有深度的认识,而我只有道听途说的浅薄印象和全是失败和不足的经历,活生生说成了长达两分钟的自我检讨和反省。自己不行,期待别人可怜,最后是没有结果的。毕竟,正如来招生的学长所说,清华注重公平性,而文化课又相对是比较公平的评判标准,所以还得我文化课争点气。
出身鄂西北小山沟,在省级贫困县成长,在高中之前从未看到过天空的这样一个可怜的孩子,在学竞赛的时候被举起来了。在离清北(梦想?)最近的时候拼了一把,然后被告知所作之事全都是无用功,可以说是我至今受到的第二大的打击了。虽然从实用性的角度考察,竞赛并没有给我带来一点点优势,反而创造了更大的差距,但是我倒是很乐在其中,也没有很后悔。
并没有从迷茫中走出来,并没有比以前变得更优秀,并比不起好友列表的dalao们,并不出众没有特长,并没有很多次尝到过成功的喜悦,并没有突破地理限制,并没有创造奇迹。我大概就是这样的一个人,努力没什么回报,倒是留给了我很多的故事,也让我偶遇了一个把故事说下去的机会。
机会?看了这篇软文就知道了。
本文已弃坑。
(多选)有一固定轨道ABCD如图所示,AB段为四分之一光滑圆弧轨道,其半径为R,BC段是水平光滑轨道,CD段是光滑斜面轨道,BC和斜面CD间用一小段光滑圆弧连接.有编号为1、2、3、4完全相同的4个小球(小球不能视为质点,其半径r<R),紧挨在一起从圆弧轨道上某处由静止释放,经平面BC到斜面CD上,忽略一切阻力,则下列说法正确的是
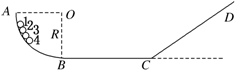
A. 四个小球在整个运动过程中始终不分离
B. 当四个小球在圆弧轨道上运动时,2号球对3号球不做功
C. 当四个小球在圆弧轨道上运动时,2号球对3号球做正功
D. 当四个小球在CD斜面轨道上运动时,2号球对3号球做正功
【解析】
这个系统由四个小球组成,其内力的关系非常复杂,对于这类问题,通常整体法是一种比较好的分析思路。本题的过程大致为:系统在斜面上下滑,动能增加→系统经过光滑平面→系统到达右侧斜面,逐小球进入斜面。在进入斜面的过程中,每个小球会发生一定的状态改变,这是我们需要单独考虑的。
A项无论在直觉还是受力分析上都是正确的,故不赘述。
B与C项,我们发现如果只有一个小球从圆弧轨道上滑下,越高的小球滑落到同一高度时速度越快,这是由于高处切线斜率较大,速度增加较快,故此处若不存在3号球,则2号球应当比在系统中运动得更快,则2号球会推着3号球运动,完成一个能量在小球之间的传递过程,C正确。
D项,我们只需要分析该球最大高度可以达到什么位置,若我们取极端数值,令斜面倾角为90°,则排列在斜面上时竖直长度会比在圆弧面上长一些,如果高度一致,则系统重力势能会偏小,因此判断这种极端情况下,最大高度应当比初始位置高一些。
这个问题中不存在小球与系统的完全分离,但是与分离问题具有相似的分析方法,即结合使用整体-隔离法分析能量变化与运动情况,值得参考。