[SHOI2008]汉诺塔 题解
题目地址:洛谷:【P4285】[SHOI2008]汉诺塔 – 洛谷、BZOJ: …
May all the beauty be blessed.
题目地址:洛谷:【P2354】[NOI2014]随机数生成器 – 洛谷、BZOJ:Problem 3671. — [Noi2014]随机数生成器
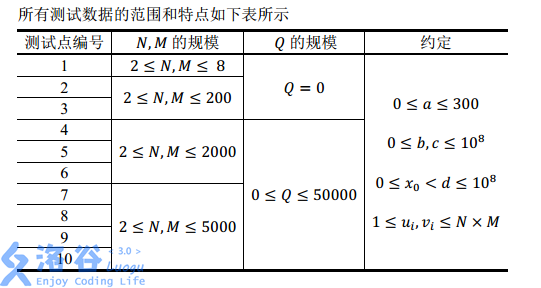
小 H 最近在研究随机算法。随机算法往往需要通过调用随机数生成函数(例如 Pascal 中的 random 和 C/C++中的 rand)来获得随机性。事实上,随机数生成函数也并不是真正的“随机”,其一般都是利用某个算法计算得来的。
比如,下面这个二次多项式递推算法就是一个常用算法:
算法选定非负整数 x0,a,b,c,d 作为随机种子,并采用如下递推公式进行计算。
对于任意 i ≥ 1, xi=(a*x[i-1]^2+b*x[i-1]+c)mod d 这样可以得到一个任意长度的非负整数数列{xi},i≥1,一般来说,我们认为这个数列是随机的。
利用随机序列{xi},i≥1,我们还可以采用如下算法来产生一个 1 到 K 的随机排列{Ti},i=1 to k:
此外,小 H 在这 K 次交换的基础上,又额外进行了 Q 次交换操作,对于第i 次额外交换,小 H 会选定两个下标 ui 和 vi,并交换 T[ui] 和 T[vi] 的值。
为了检验这个随机排列生成算法的实用性,小 H 设计了如下问题:
小 H 有一个 N 行 M 列的棋盘,她首先按照上述过程,通过 N × M + Q 次交换操作,生成了一个 1~N × M 的随机排列 {Ti},i=1 to N*M,然后将这 N × M 个数逐行逐列依次填入这个棋盘:也就是第 i 行第 i 列的格子上所填入的数应为 T[(i-1)*M+uj]。
接着小 H 希望从棋盘的左上角,也就是第一行第一列的格子出发,每次向右走或者向下走,在不走出棋盘的前提下,走到棋盘的右下角,也就是第 N 行第M 列的格子。
小 H 把所经过格子上的数字都记录了下来,并从小到大排序,这样,对于任何一条合法的移动路径,小 H 都可以得到一个长度为 N + M − 1 的升序序列,我们称之为路径序列。
小 H 想知道,她可能得到的字典序最小的路径序列应该是怎样的呢?
我们有一个随机序列生成算法,对于给定的$x_0, a, b, c, d$,有$x_i = (ax_{i-1}^2 + bx_{i-1} + c) \bmod d$。我们可以利用序列$x_i$来生成随机排列$T_i$,对于一个长为$k$的顺序排列$T_i$,我们进行$k$次交换,每次交换$T_i$和$T_{x_i \bmod i + 1}$。
我们有一个$n \times m$的矩阵,现在,我们按照上面的方法生成一个$n \times m$的随机排列,另外,给出$q$次额外交换,每次交换排列中$T_{u_i}$和$T_{v_i}$两个位置。然后,把这个排列放进矩阵中,即,矩阵$A$的元素$A_{i, j}$上填入$T_{(i-1)m+j}$。
现在,我们需要找到一条从矩阵左上角$(1, 1)$出发,每次向右或向下走一格,到右下角$(n, m)$的路径,这条路径上经过的格子的数字构成了一个长度$n+m-1$的序列,现在想求排序后字典序最小的这样的序列。
输入格式:
第1行包含5个整数,依次为 x_0,a,b,c,d ,描述小H采用的随机数生成算法所需的随机种子。
第2行包含三个整数 N,M,Q ,表示小H希望生成一个1到 N×M 的排列来填入她 N 行 M 列的棋盘,并且小H在初始的 N×M 次交换操作后,又进行了 Q 次额外的交换操作。
接下来 Q 行,第 i 行包含两个整数 u_i,v_i,表示第 i 次额外交换操作将交换 T_(u_i )和 T_(v_i ) 的值。
输出格式:
输出一行,包含 N+M-1 个由空格隔开的正整数,表示可以得到的字典序最小的路径序列。
输入样例#1:
1 3 5 1 71 3 4 3 1 7 9 9 4 9
输出样例#1:
1 2 6 8 9 12
输入样例#2:
654321 209 111 23 70000001 10 10 0
输出样例#2:
1 3 7 10 14 15 16 21 23 30 44 52 55 70 72 88 94 95 97
输入样例#3:
123456 137 701 101 10000007 20 20 0
输出样例#3:
1 10 12 14 16 26 32 38 44 46 61 81 84 101 126 128 135 140 152 156 201 206 237 242 243 253 259 269 278 279 291 298 338 345 347 352 354 383 395
对于样例 1,根据输入的随机种子,小 H 所得到的前 12 个随机数xi为:
9 5 30 11 64 42 36 22 1 9 5 30
根据这 12 个随机数,小 H 在进行初始的 12 次交换操作后得到的排列为:
6 9 1 4 5 11 12 2 7 10 3 8
在进行额外的 3 次交换操作之后,小 H 得到的最终的随机排列为:
12 9 1 7 5 11 6 2 4 10 3 8
棋盘为
12 9 1 7 5 11 6 2 4 10 3 8
最优路径依次经过的数字为 :12-9-1-6-28。
略有些无聊的卡空间阅读题。
首先,我们按照题目的要求处理出$T_i$,然后,发现开三个$5000 \times 5000$的int数组显然会爆炸,于是我们考虑重复利用最开始的$x_i$数组来存储每个数在$T_i$中的下标。
显然我们可以从小到大贪心地选择每个可行的数字,选择一个数字会对它所在行之前行可选择的列的右端点左移至该数所在列,且之后行可选择的列的左端点右移至该数所在列,我们开两个$5000$大小的int数组来存每一行能选择的列区间即可。
复杂度$O(nm)$,卡常卡空间,尽量控制吧。
// Code by KSkun, 2018/7
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
typedef long long LL;
inline int min(int a, int b) {
return a < b ? a : b;
}
inline int max(int a, int b) {
return a > b ? a : b;
}
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = (res << 1) + (res << 3) + c - '0';
return res * neg;
}
const int MAXN = 5005;
LL a, b, c, d;
int n, m, q, x[MAXN * MAXN], T[MAXN * MAXN], l[MAXN], r[MAXN];
int main() {
x[0] = readint(); a = readint(); b = readint(); c = readint(); d = readint();
n = readint(); m = readint(); q = readint();
for(int i = 1; i <= n * m; i++) {
x[i] = (1ll * a * x[i - 1] * x[i - 1] + 1ll * b * x[i - 1] + c) % d;
}
for(int i = 1; i <= n * m; i++) {
T[i] = i;
}
for(int i = 1; i <= n * m; i++) {
std::swap(T[i], T[x[i] % i + 1]);
}
while(q--) {
int u = readint(); int v = readint();
std::swap(T[u], T[v]);
}
for(int i = 1; i <= n * m; i++) {
x[T[i]] = i;
}
for(int i = 1; i <= n; i++) {
r[i] = m + 1;
}
int cnt = 0;
for(int i = 1; i <= n * m; i++) {
int X = x[i] / m + 1, Y = x[i] % m;
if(!Y) { X--; Y += m; }
if(Y >= l[X] && Y <= r[X]) {
printf("%d ", i); cnt++;
for(int j = 1; j <= n; j++) {
if(j < X) r[j] = min(r[j], Y);
if(j > X) l[j] = max(l[j], Y);
}
}
if(cnt >= n * m - 1) break;
}
return 0;
}
题目地址:洛谷:【P3649】[APIO2014]回文串 – 洛谷、BZOJ:Problem 3676. — [Apio2014]回文串
考虑一个只包含小写拉丁字母的字符串s。我们定义s的一个子串t的“出现值”为t在s中的出现次数乘以t的长度。请你求出s的所有回文子串中的最大出现值。
输入格式:
输入只有一行,为一个只包含小写字母(a-z)的非空字符串s。
输出格式:
输出一个整数,为所有回文子串的最大出现值。
输入样例#1:
abacaba
输出样例#1:
7
输入样例#2:
www
输出样例#2:
4
【样例解释1】
用 ∣s∣ 表示字符串 s 的长度。
一个字符串 s1s2…s∣s∣ 的子串是一个非空字符串 sisi+1…sj ,其中 1≤i≤j≤∣s∣ 。每个字符串都是自己的子串。
一个字符串被称作回文串当且仅当这个字符串从左往右读和从右往左读都是相同的。
这个样例中,有 7 个回文子串 a,b,c,aba,aca,bacab,abacaba。他们的存在值分别为 4,2,1,6,3,5,7 。
所以回文子串中最大的存在值为 7 。
第一个子任务共 8 分,满足 1≤∣s∣≤100 。
第二个子任务共 15 分,满足 1≤∣s∣≤1000 。
第三个子任务共 24 分,满足 1≤∣s∣≤10000 。
第四个子任务共 26 分,满足 1≤∣s∣≤100000 。
第五个子任务共 27 分,满足 1≤∣s∣≤300000 。
回文自动机直接做就行了,注意小回文串的siz值要加上大回文串的siz值,因此可以倒序(拓扑序)遍历PAM更新答案。
复杂度$O(n)$。
参考资料:「BZOJ3676」[Apio2014] 回文串 – 后缀自动机 – manacher – hzwer.com
// Code by KSkun, 2018/6
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
typedef long long LL;
const int MAXN = 300005;
int n;
char s[MAXN];
LL ans;
struct PalindromeAutomaton {
int ch[MAXN][26], fail[MAXN], len[MAXN], siz[MAXN], tot, lst;
PalindromeAutomaton() {
tot = 1; fail[0] = fail[1] = 1; len[1] = -1;
}
inline void extend(int c, int n) {
int p = lst;
while(s[n - len[p] - 1] != s[n]) p = fail[p];
if(!ch[p][c]) {
int now = ++tot, k = fail[p];
len[now] = len[p] + 2;
while(s[n - len[k] - 1] != s[n]) k = fail[k];
fail[now] = ch[k][c]; ch[p][c] = now;
}
lst = ch[p][c]; siz[lst]++;
}
inline void solve() {
for(int i = tot; i; i--) {
siz[fail[i]] += siz[i];
ans = std::max(ans, 1ll * siz[i] * len[i]);
}
}
} pam;
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
for(int i = 1; i <= n; i++) {
pam.extend(s[i] - 'a', i);
}
pam.solve();
printf("%lld", ans);
return 0;
}
题目地址:Codeforces:Problem – 916E – Codeforces、洛谷:【CF916E】Jamie and Tree – 洛谷
To your surprise, Jamie is the final boss! Ehehehe.
Jamie has given you a tree with n vertices, numbered from 1 to n. Initially, the root of the tree is the vertex with number 1. Also, each vertex has a value on it.
Jamie also gives you three types of queries on the tree:
1 v — Change the tree’s root to vertex with number v.
2 u v x — For each vertex in the subtree of smallest size that contains u and v, add x to its value.
3 v — Find sum of values of vertices in the subtree of vertex with number v.
A subtree of vertex v is a set of vertices such that v lies on shortest path from this vertex to root of the tree. Pay attention that subtree of a vertex can change after changing the tree’s root.
Show your strength in programming to Jamie by performing the queries accurately!
给你一棵有根树,最开始根是1,点上有点权,三种操作:
输入格式:
The first line of input contains two space-separated integers n and q (1 ≤ n ≤ 10^5, 1 ≤ q ≤ 10^5) — the number of vertices in the tree and the number of queries to process respectively.
The second line contains n space-separated integers a1, a2, …, an ( - 10^8 ≤ ai ≤ 10^8) — initial values of the vertices.
Next n - 1 lines contains two space-separated integers ui, vi (1 ≤ ui, vi ≤ n) describing edge between vertices ui and vi in the tree.
The following q lines describe the queries.
Each query has one of following formats depending on its type:
1 v (1 ≤ v ≤ n) for queries of the first type.
2 u v x (1 ≤ u, v ≤ n, - 10^8 ≤ x ≤ 10^8) for queries of the second type.
3 v (1 ≤ v ≤ n) for queries of the third type.
All numbers in queries’ descriptions are integers.
The queries must be carried out in the given order. It is guaranteed that the tree is valid.
输出格式:
For each query of the third type, output the required answer. It is guaranteed that at least one query of the third type is given by Jamie.
输入样例#1:
6 7 1 4 2 8 5 7 1 2 3 1 4 3 4 5 3 6 3 1 2 4 6 3 3 4 1 6 2 2 4 -5 1 4 3 3
输出样例#1:
27 19 5
输入样例#2:
4 6 4 3 5 6 1 2 2 3 3 4 3 1 1 3 2 2 4 3 1 1 2 2 4 -3 3 1
输出样例#2:
18 21
The following picture shows how the tree varies after the queries in the first sample.
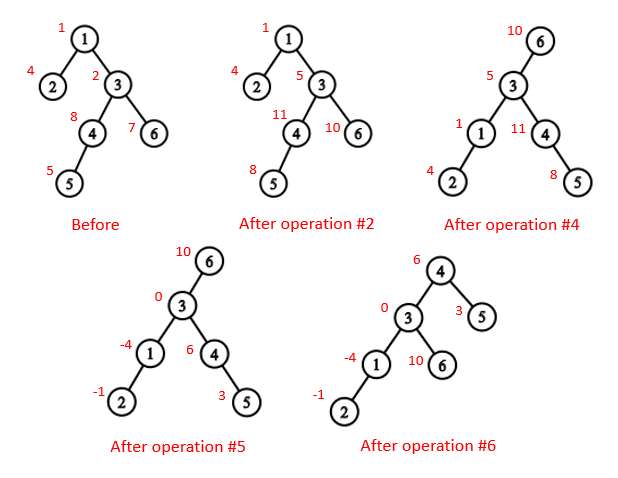
雅礼集训Day 1 Prob 1,然而并没能A掉。
换根用LCT做比较快,而子树和用DFS序线段树做比较快。我们要从里面选择一种方法实现。
LCT做的话,需要用到维护子树(包含虚边连的子树)信息的LCT,还要用LCT实现找LCA的算法。具体做法是,找access u和access v路径上最深的相同点。
用线段树做会好写一些,换根对子树加法求和的影响实际上可以讨论出来。试想一条现在根(即1)到换根后的根的路径,对于子树加法的操作,如果u到v的路径与当前根到1的路径无交集时,换根对它产生不了影响,例如样例1中,换根到6后的u=4, v=5这个点对就属于该种情况,这种情况的判定是u和v在根为1的树(下称原树)的LCA与现在的根再求一次LCA,若得到的结果不是原来的LCA,说明属于此种情况;反之,我们需要找到两条路径交集中最深的那个点,可以在LCA(u, rt)和LCA(v, rt)中取最深点,这个点在换根后的树上是最浅的点,子树加法时,只需要加这个点上面的那部分即可,即全树加x,再在当前根到1的路径上的这个点的子节点对应的子树处-x即可,查询同理加全树减这一部分权值即可。
需要保证操作是严格$O(\log n)$的否则会被卡,复杂度$O(n \log n)$。
// Code by KSkun, 2018/6
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <vector>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = (res << 1) + (res << 3) + c - '0';
return res * neg;
}
const int MAXN = 100005;
std::vector<int> gra[MAXN];
int n, q, a[MAXN];
int fa[MAXN], siz[MAXN], son[MAXN], dep[MAXN];
inline void dfs1(int u) {
siz[u] = 1;
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(v == fa[u]) continue;
fa[v] = u; dep[v] = dep[u] + 1;
dfs1(v); siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
}
int top[MAXN], dfn[MAXN], vn[MAXN], clk;
inline void dfs2(int u, int tp) {
dfn[u] = ++clk; vn[dfn[u]] = u; top[u] = tp;
if(son[u]) dfs2(son[u], tp);
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
inline int querylca(int u, int v) {
int tu = top[u], tv = top[v];
while(tu != tv) {
if(dep[tu] > dep[tv]) {
std::swap(u, v); std::swap(tu, tv);
}
v = fa[tv]; tv = top[v];
}
if(dep[u] < dep[v]) return u; else return v;
}
LL sum[MAXN << 2], tag[MAXN << 2];
#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)
inline void build(int o, int l, int r) {
if(l == r) {
sum[o] = a[vn[l]]; return;
}
build(lch, l, mid);
build(rch, mid + 1, r);
sum[o] = sum[lch] + sum[rch];
}
inline void pushdown(int o, int l, int r) {
if(tag[o]) {
tag[lch] += tag[o]; tag[rch] += tag[o];
sum[lch] += tag[o] * (mid - l + 1); sum[rch] += tag[o] * (r - mid);
tag[o] = 0;
}
}
inline void add(int o, int l, int r, int ll, int rr, LL v) {
if(l >= ll && r <= rr) {
sum[o] += v * (r - l + 1); tag[o] += v; return;
}
pushdown(o, l, r);
if(ll <= mid) add(lch, l, mid, ll, rr, v);
if(rr > mid) add(rch, mid + 1, r, ll, rr, v);
sum[o] = sum[lch] + sum[rch];
}
inline LL query(int o, int l, int r, int ll, int rr) {
if(l >= ll && r <= rr) return sum[o];
pushdown(o, l, r); LL res = 0;
if(ll <= mid) res += query(lch, l, mid, ll, rr);
if(rr > mid) res += query(rch, mid + 1, r, ll, rr);
return res;
}
int rt = 1;
int main() {
n = readint(); q = readint();
for(int i = 1; i <= n; i++) {
a[i] = readint();
}
for(int i = 1, u, v; i < n; i++) {
u = readint(); v = readint();
gra[u].push_back(v); gra[v].push_back(u);
}
dfs1(1); dfs2(1, 1); build(1, 1, n);
while(q--) {
int op, u, v, x;
op = readint();
if(op == 1) {
rt = readint();
} else if(op == 2) {
u = readint(); v = readint(); x = readint();
int lca = querylca(u, v), l1 = querylca(u, rt), l2 = querylca(v, rt);
if(rt == 1 || querylca(lca, rt) != lca) {
add(1, 1, n, dfn[lca], dfn[lca] + siz[lca] - 1, x);
} else {
lca = dep[l1] > dep[l2] ? l1 : l2;
add(1, 1, n, 1, n, x);
if(lca != rt) {
int p = rt;
while(dep[fa[top[p]]] > dep[lca]) p = fa[top[p]];
p = vn[dfn[p] - (dep[p] - dep[lca] - 1)];
add(1, 1, n, dfn[p], dfn[p] + siz[p] - 1, -x);
}
}
} else {
u = readint();
if(rt == 1 || querylca(u, rt) != u) {
printf("%lld\n", query(1, 1, n, dfn[u], dfn[u] + siz[u] - 1));
} else {
LL res = 0;
res += query(1, 1, n, 1, n);
if(u != rt) {
int p = rt;
while(dep[fa[top[p]]] > dep[u]) p = fa[top[p]];
p = vn[dfn[p] - (dep[p] - dep[u] - 1)];
res -= query(1, 1, n, dfn[p], dfn[p] + siz[p] - 1);
}
printf("%lld\n", res);
}
}
}
return 0;
}