[APIO2015]巴厘岛的雕塑 题解
题目地址:洛谷:【P3646】[APIO2015]巴厘岛的雕塑 – 洛谷、BZ …
May all the beauty be blessed.
题目地址:HDUOJ:Problem – 3022、Timus Online Judge:1658. Sum of Digits @ Timus Online Judge
Petka thought of a positive integer n and reported to Chapaev the sum of its digits and the sum of its squared digits. Chapaev scratched his head and said: “Well, Petka, I won’t find just your number, but I can find the smallest fitting number.” Can you do the same?
给定一个数字每位上数字的和和平方和,求符合条件的最小数字。
输入格式:
The first line contains the number of test cases t (no more than 10000). In each of the following t lines there are numbers s1 and s2 (1 ≤ s1, s2 ≤ 10000) separated by a space. They are the sum of digits and the sum of squared digits of the number n.
输出格式:
For each test case, output in a separate line the smallest fitting number n, or “No solution” if there is no such number or if it contains more than 100 digits.
输入样例#1:
4 9 81 12 9 6 10 7 9
输出样例#1:
9 No solution 1122 111112
是一个很巧妙的DP。
首先s1≤900,s2≤8100是很好确定的。大于的情况直接无解。
首先,考虑两个DP,f[i][j]代表和为i平方和为j的数字最小长度,g[i][j]代表和为i平方和为j的最小开头数字。容易知道最优解数字中肯定不含0。
我们枚举i和j,然后从小到大枚举扩展长度的数字k,如果在f[i][j]的基础上加入k后长度比f[i+k][j+k*k]更小,那么应当更新答案,此时k也就是g[i][j]的值。如果加入k后与f[i+k][j+k*k]长度一样,那么g[i][j]看一下是否比k大,更新g[i][j]答案。这是一个很暴力的转移。
上面的两个DP数组可以预处理出来,查询的时候先看是否可行,是否超100,然后每次用g[i][j]输出,s1-=g[i][j],s2-=g[i][j]*g[i][j],直到s1或s2为0。
// Code by KSkun, 2018/3
#include <cstdio>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int readint() {
register int res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN1 = 910, MAXN2 = 8110;
int T, s1, s2, f[MAXN1][MAXN2], g[MAXN1][MAXN2];
inline int sqr(int x) {
return x * x;
}
inline void init() {
for(int i = 1; i <= 9; i++) {
f[i][sqr(i)] = 1;
g[i][sqr(i)] = i;
}
for(int i = 1; i <= 900; i++) {
for(int j = 1; j <= 8100; j++) {
if(f[i][j]) {
for(int k = 1; k <= 9; k++) {
if(!f[i + k][j + sqr(k)] || f[i + k][j + sqr(k)] > f[i][j] + 1) {
f[i + k][j + sqr(k)] = f[i][j] + 1;
g[i + k][j + sqr(k)] = k;
} else if(f[i + k][j + sqr(k)] == f[i][j] + 1) {
g[i + k][j + sqr(k)] = std::min(g[i + k][j + sqr(k)] = k, k);
}
}
}
}
}
}
int main() {
T = readint();
init();
while(T--) {
s1 = readint();
s2 = readint();
if(s1 > 900 || s2 > 8100 || !f[s1][s2] || f[s1][s2] > 100) {
printf("No solution\n");
continue;
}
while(s1 && s2) {
int t = g[s1][s2];
printf("%d", t);
s1 -= t;
s2 -= sqr(t);
}
printf("\n");
}
return 0;
}
题目地址:ZCMU:Power Eggs
Benedict bought K identical power eggs from Dropeggs.com, and now he wants to test them by dropping them from different floors of his building. His building has N floors numbered 1 to N. F is an unknown number in the range from 0 to N, inclusive. Each egg will break if dropped from floor F+1 or above, but will not break if dropped from floor F or below. Benedict can drop each egg as many times as he wants from any floor until it breaks. He wants to know the minimum number of egg drops necessary to ensure that he can determine F.
For example, if there are three floors and Benedict has only one egg, then he has to first throw the egg from the first floor, then from the second floor (if the egg survived), and then from the third floor (if the egg survived). Therefore, three drops are required in the worst case.
有K个鹰蛋N层楼,鹰蛋从1~F层楼掉下来不会碎,F+1层及以上掉下来会碎,要求求确定F值最坏情况下的最小值。
输入格式:
The first line contains one number T (1 ≤ T ≤ 10000) which is the number of test cases, followed by T lines. Each of the next T lines contains two numbers: N, the number of floors (1 ≤ N ≤ 2000000007) and K, the number of eggs (1 ≤ K ≤ 32).
输出格式:
For each of the T lines, print the minimal number of drops required, or if it’s greater than 32, print the word Impossible. After that many drops, Benedict gets too tired and cannot continue.
输入样例#1:
4 10 1 100 2 30 30 2000000000 2
输出样例#1:
10 14 5 Impossible
其实把这个题放在这最重要的不是这个题,而是下面这个ppt的内容。
算法合集之《从《鹰蛋》一题浅析对动态规划算法的优化》.ppt
好的我们来说一下这题最后的解法。DP状态是dp[i][j]表示i个鹰蛋尝试j次最多能确定几层楼的情况。转移方程如下
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] + 1
如果这颗蛋碎了,剩下的蛋能确定的层数是第一项,如果没碎则是第二项。
初始值dp[1][j]=1,dp[i][1]=i。
对于可以交的这个题来说,预处理出32个蛋32次就可以做了。因为DP值具有单调性,甚至可以二分找到答案。
所以说这个题的意义不是去AC它,而是看上面那个PPT的内容啊!
如果是个老实的DP题,算法复杂度O(n \log n)
// Code by KSkun, 2018/3
#include <cstdio>
#include <algorithm>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int readint() {
register int res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 35;
int T;
LL n, k, dp[MAXN][MAXN];
int main() {
for(int i = 1; i <= 32; i++) {
dp[1][i] = i;
dp[i][1] = 1;
}
for(int i = 2; i <= 32; i++) {
for(int j = 2; j <= 32; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1] + 1;
}
}
T = readint();
while(T--) {
n = readint();
k = readint();
int res = std::lower_bound(dp[k] + 1, dp[k] + 33, n) - dp[k];
if(res > 32) printf("Impossible\n"); else printf("%d\n", res);
}
return 0;
}
题目地址:TopCoder Arena:Practice – TopCoder Arena、vjudge:MaximalTriangle – TopCoder 12054 – Virtual Judge
You are given ints n and z. We have a regular n-gon: a convex polygon with n sides, in which all sides have the same length and all internal angles are equal. We want to draw (n-3) non-intersecting diagonals in some way. Once we do that, we will have the polygon divided into exactly (n-2) triangles. We want to produce a situation in which one of these (n-2) triangles has a strictly larger area than each of the remaining (n-3).
The vertices of the polygon are labeled 1 through n in clockwise order. Two sets of diagonals are different if one of them contains a diagonal that is not present in the other one. Count all sets of (n-3) non-intersecting diagonals that produce an arrangement with the above property. Return that count modulo z.
求一个正n边形的三角剖分方案中面积最大的三角形唯一的方案数。给出n和模数k。
类名:MaximalTriangle
函数名:howMany
参数:int, int
返回值:int
函数声明:int howMany(int n, int z)
样例#1:
4 1000000000
样例#1结果:
0
其他样例参见原网站。
n will be between 3 and 444, inclusive.
z will be between 1 and 1,000,000,000 (10^9), inclusive.
其实这个题把我折磨了一下午。官方题解只有文字(英文)没有程序,我半天想不出来怎么写,然后学习使用TopCoder Arena进Practice Room抄代码才解决了这个题。在这里推荐各位在vjudge上交,TC真的很难学。附官方题解:SRM 547 – TopCoder Wiki。这道题是SRM 547 Div 1 Level 3。
让我们从浅入深地揭示这个出题人卡常毒瘤的实质。
首先,我们考虑最开始的想法,就是想一种动规去解决这个问题。我们考虑枚举面积最大的那个三角形,它最多将多边形分为3块,就像下面这个多边形。
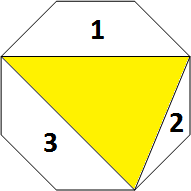
我们分别对这三块进行DP处理里面的三角剖分方案。我们考虑类似卡特兰数的计算方法,在一块中先找一个面积小于最大三角形的三角形,然后它会把这块再割成两块,再乘法原理将两块的答案乘起来。定义dp[i]为跨越i条边的一块的三角剖分方案数,转移方程即
dp[i] = \sum (dp[j] * dp[i - j])
如果我们给顶点命名为A1…An,那么上式能够转移的条件是A1、Ai、Aj组成的三角形面积小于最大三角形。
最后的答案应该是枚举的每一种三角形的三边跨越的边数的dp值乘起来,再把每种枚举情况的答案加起来。
枚举需要O(n^2)复杂度,而DP也需要O(n^2),因此总体复杂度应该是O(n^4)的。但是这会被毒瘤出题人卡掉常数。下面就是一些官方提供的卡常手段。
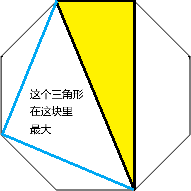
unsigned long long可以存很大的数,不用每乘一次都取模,可以考虑乘多个几次,到快超了的时候再取模,具体而言,这个题比较安全的分界点是8 \times 10^{18}。上面就是官方提供的卡常办法。实际上这个题的实现难度也是有的。比如快速搞出来正多边形内部各种三角形的面积。下面是这一段的代码。
for(int i = 0; i < n; i++) {
ang[i] = 2 * PI * i / n ;
}
for(int i = 1; i < n; i++) {
for(int j = 1; j < n - i; j++) {
area[i][j] = fabs(sin(ang[i]) + sin(ang[j]) - sin(ang[i + j]));
}
}
area[i][j]的意思是规定一个点不变,从这个点顺时针走i条边到达的顶点和逆时针走j条边到达的顶点(当然你可以反着定义)三个点构成的三角形的一个面积的表示。这个的原理是什么呢。我们看下面这张图。
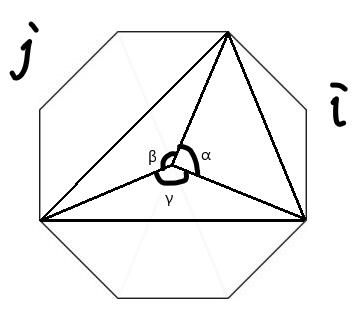
实际上在这个图里,若我们规定这个正八边形的中心到各顶点的距离为1,以α为内角的三角形面积为\frac{1}{2} \sin \alpha,相似地,剩下两个小三角形面积分别为\frac{1}{2} \sin \beta、\frac{1}{2} \sin \gamma。我们观察到\gamma = 2 \pi - \alpha - \beta,而\alpha = \frac{2 \pi}{n} \cdot i, \beta = \frac{2 \pi}{n} \cdot j, 2 \pi - \gamma = \frac{2 \pi}{n} \cdot (i + j)。那么我们把每个\sin(\frac{2 \pi}{n} \cdot i)都处理出来不就好办了嘛。至于上面的1/2,就不管它了,反正这个值能代表这个三角形的面积。
剩下的实现并不是很有难度,但是优化难理解。可以对照代码注释和上面的卡常手段一起对比理解。
由于TopCoder要求实现一个class,下面的代码并不是标准输入/输出格式(传统OI题目)的实现方式,但是把调试注释给去掉就可以用标准输入/输出了。
// Code by KSkun, 2018/3
//#include <cstdio>
#include <cmath>
#include <cstring>
typedef long long LL;
const int MAXN = 505;
const double PI = 2 * acos(0.0), EPS = 1e-9;
const LL INF = 8e18;
class MaximalTriangle {
public:
int MO;
double ang[MAXN], area[MAXN][MAXN];
LL cat[MAXN], dp[MAXN];
inline void add(LL &x, LL y) {
x += y;
if(x >= INF) x %= MO;
}
void caldp(double s, int m) {
dp[0] = 0;
dp[1] = 1 % MO; // 这是出题人的一个坑,模数可以为1,但是其实我很反感这种坑,考着玩可以,但是这根算法真的没啥关系吧
for(int i = 2; i <= m; i++) {
int mid = i / 2;
if(area[mid][i - mid] + EPS < s) { // “中间位置”的三角形最大,如果这个三角形都比最大三角形小,那么直接取卡特兰数
dp[i] = cat[i];
continue;
}
dp[i] = 0;
for(int j = 1; area[j][i - j] + EPS < s; j++) {
add(dp[i], dp[j] * dp[i - j]); // 如果当前枚举到的这个三角形符合条件,那么可以DP转移
}
dp[i] %= MO;
dp[i] += dp[i]; // 重复一遍,因为转移的情况是对称的,可以避免重复计算
dp[i] %= MO;
}
}
int howMany(int n, int z) {
MO = z;
// 下面是预处理卡特兰数
memset(cat, 0, sizeof cat);
cat[1] = 1 % MO;
for(int i = 2; i <= n; i++) {
for(int j = 1; j < i; j++) {
add(cat[i], cat[j] * cat[i - j]);
}
cat[i] %= MO;
}
// 下面是预处理各种三角形的面积
for(int i = 0; i < n; i++) {
ang[i] = 2 * PI * i / n ;
}
for(int i = 1; i < n; i++) {
for(int j = 1; j < n - i; j++) {
area[i][j] = fabs(sin(ang[i]) + sin(ang[j]) - sin(ang[i + j]));
}
}
// 下面是解题的核心
LL ans = 0;
for(int i = 1; i < n; i++) {
for(int j = i; j < n - i; j++) {
int k = n - i - j, comb = n; // i, j, k分别代表最大三角形三边分别跨越了多少原多边形的边
if(k < j) continue; // 总是使i, j, k递增,保证枚举的情况不重
if(i == j && j == k) comb /= 3; // 如果发现是正三角形,那么旋转n次中会有2/3的情况重叠
if(i != j && j != k) comb *= 2; // 如果发现三条边都不一样,那么把这个情况对称过来又是一种情况,这里避免重复计算
caldp(area[i][j], k);
add(ans, (comb * dp[i] % MO) * (dp[j] * dp[k] % MO));
}
}
return ans % MO;
}
};
/*int main() {
MaximalTriangle t;
int n, z;
scanf("%d%d", &n, &z);
printf("%d", t.howMany(n, z));
return 0;
}*/