2020年12月25日

随机数生成算法与其图形应用

随机数生成算法与其图形应用

By KSkun, 2020/12

注：由于本文章面向非专业读者，其中的描述可能不够准确。需要获取准确的说明请阅读参考资料等。

什么是随机数

随机数是一种在各种行业中被广泛应用的工具。在密码学中，我们利用随机数生成随机密钥；在图形学中，我们利用随机数进行蒙特卡洛积分，计算渲染的结果；在统计学中，我们利用随机数进行抽样调查，减小统计的工作量。

对于随机数的不同用途，我们对随机数的要求不一，因此随机数也存在着多种定义[1]：

  • 统计学伪随机数：指生成的随机数大致均匀分布在其取值空间中。 例如，对于统计学伪随机数比特流而言，其均匀分布即样本中的 1 与 0 的数量大致相同；对于在二维有限空间中生成的统计学伪随机数点而言，图 1-1 是较均匀的分布。
  • 密码学安全伪随机数：指取得随机数样本的一部分，不能轻易计算出样本的剩余部分。 在密码学中，随机数通常用于生成成对或成组的密钥，如果随机数样本可以预测，则获得其中的一部分密钥，其余密钥也有被破解的风险。
  • 真随机数：随机样本不可重现。 由量子力学可知，在自然界中存在具有真随机性的现象，但我们很难采集这些随机性；常用的随机性通过物理噪音采集，但也只是接近理想的真随机数。
289px Sobol sequence 2D.svg - 随机数生成算法与其图形应用
图 1.1 利用 Sobol 序列生成的二维随机数点[2]

以上三个随机数的条件是逐渐增强的，获得它们的难度也是逐渐增加的。因此我们需要面向随机数的使用场景选择合适的随机数产生方式，以实现安全性与性能的最佳匹配。

噪声也很有用：真随机数的获取与使用

真随机数的获取机理

真随机数生成器（True Random Number Generator，TRNG）用于生成真正的随机数，即不可预测、不可重现的随机数。目前应用中的真随机数大多来自于物理定律保证的随机性，根据原理可以分为量子和经典两种类型。接下来分别简单介绍两种随机性的采集。[3]

量子随机性

量子随机性的来源主要可以分为两类：原子或更小尺度的量子现象，如原子的衰变；或热噪声，如气体分子的碰撞。以下是一些可以被采集的量子随机性源：

  • 散粒噪声（Shot Noise）：观测微观粒子时，样本数量足够小时，可以观测到数据产生涨落变化，这种涨落便是散粒噪声。如可以用光电二极管采集光源的光子，由于不确定性原理，光子作用在二极管上会在电路中产生噪声；
  • 衰变辐射源：原子的衰变是随机过程。可以用盖革计数器采集这种衰变的随机性；
  • 晶体管实现的放大电路：在使用晶体管放大信号时，发射极富含电子，这些电子偶尔会穿越势垒从基极离开，可以使用放大电路放大这一随机性并采集。

经典随机性

经典随机性通常来源于热现象，但由于温度越高热现象越剧烈，降低温度可能会减少热随机性。以下是一些可以被采集的热随机性源：

  • 热噪声（Johnson-Nyquist Noise）：导体内部的电荷在热运动时产生的电噪声，可以通过放大电路放大并采集；[4]
  • 二极管的击穿：齐纳二极管通常工作在反向击穿区起稳压作用，击穿时也会产生噪声；
  • 大气噪声：环境中存在形式为电磁波的噪声，可以通过一个无线电接收器采集。

Linux 中的真随机数：/dev/random

Linux 中存在两个与随机数相关的虚拟设备：/dev/random 与 /dev/urandom。这两个设备可以输出随机比特流，用户也可以通过输入数据增加其熵池中的熵。两个设备的区别是，当熵池中的熵低到一定程度时，前者会阻塞并等待熵增加，后者则不会阻塞，但可能导致输出的随机性较差。

Linux 的这些设备可以认为是真随机数生成器。其随机性来源自计算机系统运行中的噪声，具体而言，是 IO 操作的时间戳。磁盘、网络以及键盘、鼠标等设备的输入时间戳会被捕捉，并截取其毫秒或微秒部分的数值，这一部分的数值通常具有随机性。[5]

采集到随机性后，系统将其与熵池中的现有熵进行一系列数学组合，增加熵池中的熵。在生成随机数时，系统使用 SHA-1 对整个熵池计算散列值，这个值便是随机数的输出。

统计学工具：准随机数生成器

蒙特卡洛方法往往需要均匀分布在一定空间中的随机数，准随机数生成器（Quasi-Random Number Generator，QRNG）便是用于生成这样一系列随机数的工具。具体而言，常用的准随机数序列包括：Halton 序列、Sobol 序列等。[6][7]这些序列在选取不同参数时，呈现出低相关性，因此可以用于生成随机数。

Van der Corput 序列

我们先给出 Van der Corput 序列的定义：给定一个正整数 $b$ 作为基，对于一个整数 $i$，其可表示为 $b$ 进制数 $i=\sum a_l(i) b^l$，则 Van der Corput 序列可以由正整数序列通过下列变换获得

$$ \mathbf{\Phi}_b(i) = (b^{-1} \ b^{-2} \ \cdots \ b^{-M}) \cdot (a_0(i) \ a_1(i) \ \cdots \ a_{M-1}(i))^{\mathbf{T}} = \sum a_l(b)\cdot b^{-(l+1)} $$

这可以看做将一个数字的 ​ 进制表示镜像翻转到小数点右侧，如下图所示是一个以 2 为基的 Van der Corput 序列的一部分：

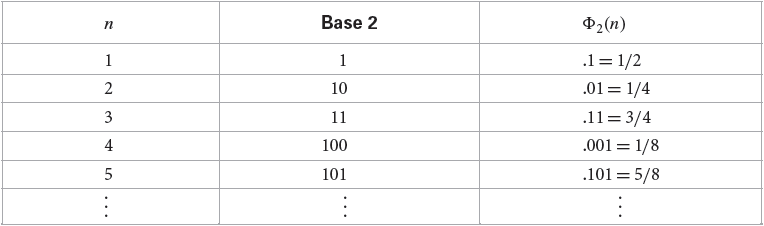
base 2 van der corput - 随机数生成算法与其图形应用
图 3-1 部分以 2 为基的 Van der Corput 序列[7]

容易发现，这个序列的每一个点都是取目前最长的未覆盖区域的中点，因此具有平均分布的特性。

Halton 序列与 Hammersley 点集

Halton 序列通过下式生成：

$$ \boldsymbol{X}_i = (\mathbf{\Phi}_{b_1}(i) \ \mathbf{\Phi}_{b_2}(i) \ \cdots \ \mathbf{\Phi}_{b_n}(i)) $$

其中，$b_1, b_2, \dots, b_n$ 取一些互质的质数。由于每一维都是一个 Van der Corput 序列，如此得到的 $n$ 维空间中的一些点在每一维上都是均匀分布的，因此其也具有均匀分布的性质。

而 Hammersley 点集通过下式生成：

$$ \boldsymbol{X}_i = \left(\dfrac{i}{N} \ \mathbf{\Phi}_{b_1}(i) \ \mathbf{\Phi}_{b_2}(i) \ \cdots \ \mathbf{\Phi}_{b_{n-1}}(i)\right) $$

它和 Halton 序列的区别只有第一维是 ​ 上均匀分布的，由于这一区别，其平均分布的性质较 Halton 序列更好。此外，生成 Hammersley 点集需要知道样本点的总数量。下图展示了数量为 100 的二维 Halton 序列和 Hammersley 点集的分布状况：

halton hammersley - 随机数生成算法与其图形应用
图 3-2 数量为 100 的二维 Halton 序列（左）[7]
图 3-3 数量为 100 的二维 Hammersley 点集（右）[7]

这些序列的缺点是，当基数选取的较大时，生成的前一些点容易呈线性相关性，如基为 17、19 的 Halton 序列的前 16 项为 $(1/17, 1/19), (2/17, 2/19), \dots, (16/17, 16/19)$。为了避免此问题，通常可以丢弃生成的前一些点，或使用一些手段打乱序列的顺序。打乱顺序并不会影响序列的平均分布性质和无关性。[8]

Sobol 序列

让我们修改一下 Van der Corput 序列的生成方式，在翻转之前先乘以一个生成矩阵 $\mathbf{C}$，即：

$$ \mathbf{\Phi}_{b,\mathbf{C}}(i) = (b^{-1} \ b^{-2} \ \cdots \ b^{-M}) \cdot [\mathbf{C} \cdot (a_0(i) \ a_1(i) \ \cdots \ a_{M-1}(i))^{\mathbf{T}}] $$

而 Sobol 序列则可以通过下式生成：

$$ \boldsymbol{X}_i = (\mathbf{\Phi}_{2,\mathbf{C}_1}(i) \ \mathbf{\Phi}_{2,\mathbf{C}_2}(i) \ \cdots \ \mathbf{\Phi}_{2,\mathbf{C}_n}(i)) $$

即，Sobol 序列的每一维都是以 2 为基的，带不同生成矩阵的类似 Van der Corput 序列。它也具有均匀分布性质，且是对于每一维的 2 的幂次等分区域都会恰好有一个样本点。为了得到分布良好的数列，且避免类似 Halton 序列前几个点出现的线性相关性，生成矩阵需要精心设计，可以在相关资料中获取设计好的生成矩阵。

很快啊，啪一下就生成了：伪随机数生成器

真随机数的获得需要采集物理现象，准随机数的获得可能需要大量运算，生成这些随机数的成本都较高。为了适应需要快速获得随机数的场景，我们可以降低对随机数性质的要求，则伪随机数生成器（Pseudo Random Number Generator，PRNG）就被提了出来。它用于生成近似具有随机数分布的特性，但可能可以通过分析预测的伪随机数，出于性能考量，其算法具有快速计算的特征。[9]

线性同余生成器

线性同余生成器（Linear Congruential Generator，LCG）生成随机数的原理基于一个迭代公式：

$$ X_{n+1}=(aX_n+c) \bmod m $$

这种算法在早期是最常用的随机数生成算法，因为其计算简单，且当时并没有发现更好的方法。例如，C 中的 rand() 函数便是以这种方法实现的。[10]

这一方法产生的随机数周期与参数 $a, c, m$ 值的选取有关，根据取模运算的性质，这一算法生成随机数的周期最多为 $m$，因此存在周期较小的问题。[11]

梅森旋转算法（梅森转转转）

梅森旋转算法（Mersenne Twister，MT）是一种于 1997 年新发明的伪随机数生成算法。该算法的运算非常适合计算，且周期达到了 $2^{19937}-1$ 规模，这个数字被称作梅森质数（Mersenne Prime），这也是该算法名的由来。[13]

为了清晰地分析 MT 算法的流程，我们先给出一个伪随机数生成器的抽象工作流程：

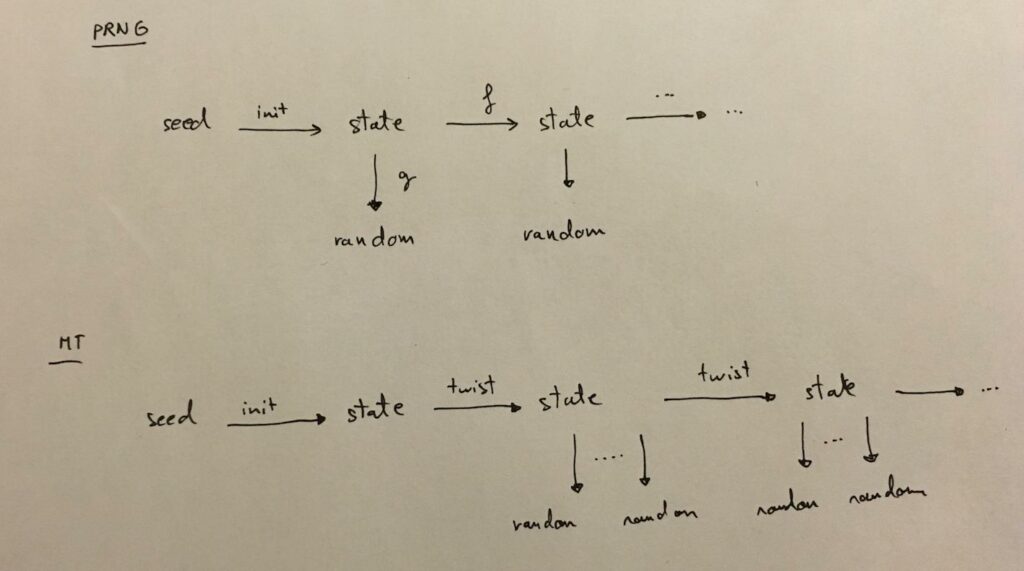
prng work flow 1024x571 - 随机数生成算法与其图形应用
图 4-1 伪随机数生成器的抽象工作流程[12]

如图所示，我们先用种子（seed）初始化一个初始状态，此时可以通过一个生成函数从状态中生成随机数，生成后通过一个转换函数将当前状态转换成下一个状态。在 MT 中，生成随机数的函数被称为 temper，转换状态的函数被称为 twist。接下来我们按照工作流的先后顺序解释算法各部分的流程[13][15]，下面给出了 MT 的全流程示意图，读者也可以结合该图理解。

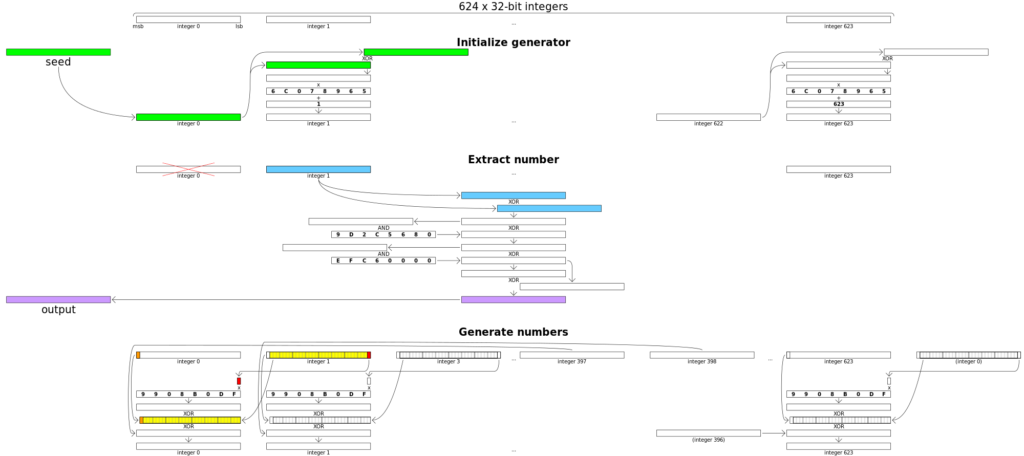
2000px Mersenne Twister visualisation.svg 1024x456 - 随机数生成算法与其图形应用
图 4-2 梅森旋转算法的全流程示意图[14]

初始化

MT 算法的工作区包含 $n$ 个 $w$ 位整数组成的数组 $x_0, x_1, \dots, x_{n-1}$，初始化的工作即是通过种子计算出这些整数的值。下式用于迭代地计算这些整数的值：

$$ x_i=f \cdot {x_{i-1} \oplus [x_{i-1} \gg (w-2)]} + i $$

其中，$\oplus$ 表示按位异或，$\gg$ 表示二进制右移，$\cdot$ 表示常规的整数乘法。通过上式即可获得初始状态的数值，但初始状态不能直接用于生成随机数，必须要经过一次 twist 转换到下一状态。

twist

twist 是 MT 的状态转换函数，其通过下式迭代地计算下一状态的值：

$$ x_{k+n} = x_{k+m} \oplus [(\operatorname{upperbits}x_k || \operatorname{lowerbits}x_{k+1}) \cdot \mathbf{A}] \ (\text{for } k: \ 0\rightarrow n-1)$$

其中，$\operatorname{upperbits}$ 代表该整数的高 $w-r$ 位（低位填 0），$\operatorname{lowerbits}$ 代表该整数的低 $r$ 位（高位填 0），$||$ 代表二进制或，在这里的作用是将高位和低位组合起来，其他记号同上。通过上式计算出的 $x_n, x_{n+1}, \dots, x_{2n-1}$ 即为下一状态的值。

这里的 $\mathbf{A}$ 是一个矩阵，如果将一个 $w$ 位的整数看成是 $w$ 维的向量，则上式中则是令此向量乘上矩阵 $\mathbf{A}$。该矩阵定义如下：

$$ \mathbf{A} = \begin{pmatrix} 0 & \mathbf{I}_{w-1} \\ a_{w-1} & (a_{w-2}, \dots, a_0) \end{pmatrix} $$

则乘上该矩阵的作用等效为下式：

$$ x\mathbf{A} = \begin{cases} x \gg 1, & x_0=0, \\ (x \gg 1) \oplus a, & x_0=1. \end{cases} $$

这一操作的设计将在之后提到。

temper

容易发现，MT 的一个状态包括了 $n$ 个整数 $x_0, x_1, \dots, x_{n-1}$，其中每一个整数都可以用于产生一个随机数，因此一个状态共可以产生 $n$ 个随机数。产生随机数时，我们取出下一个未使用的数字 $x_m$，并进行如下操作：

$$ \begin{cases} y=x\oplus[(x\gg u)\&d] \\ y=y\oplus[(y\ll s)\&b] \\ y=y\oplus [(y\ll t)\& c] \\ z=y\oplus (y\gg l) \end{cases} $$

其中 $u, s, t, b, c, d$ 都是参数，$\ll$ 和 $\gg$ 分别代表二进制左移和右移，$\&$ 代表按位与。操作后产生的 $z$ 即为此次生成的随机数。

线性反馈移位寄存器与 twist

为了解释 MT 算法的核心操作 twist，我们首先要引入一个概念：线性反馈移位寄存器（Linear Feedback Shifting Register，LFSR）。

学过数电的同学对移位寄存器的概念并不陌生，该寄存器支持存储几个位，并支持将存储的位进行左移或右移，空出来的一位通过外部输入的信号指定。而 LFSR 则是将空出来的一位通过一个反馈函数进行迭代异或来指定的，因此被称作线性反馈。

对于一个 4 位的 LFSR，有反馈函数 $f(x)=x^4+x^2+x+1$ ，则反馈应该通过高 4、2、1 位迭代异或后生成，即 $a_{\text{new}}=a_3\oplus a_1\oplus a_0$。令其初始状态为 1000，则迭代进行向右移位，其状态变化：1000→1100→1110→0111→0011→0001→1000。容易发现此处形成了一个长为 6 的状态环。

对于一个 $w$ 位的 LFSR，其最多有 $2^w$ 种可能的状态，其中全 0 是无效状态，因此有 $2^w-1$ 种有效状态。当反馈函数 $f(x)$ 满足某些条件时，可以让 LFSR 的状态环长度达到最大值 $2^w-1$。

mt lfsr - 随机数生成算法与其图形应用
图 4-3 MT 看做 LSFR 的示意图[15]

让我们回头来看 twist 的流程，它包含一个迭代进行的递推式，如果将 $x_{k+n}$ 看做 $x_{k-1}$，则可以认为 $x_{k+n}$ 便是其中的反馈位，该反馈位通过 $x_k$ 的高位和 $x_{k+1}$ 的低位拼接，再与 $x_{k+m}$ 进行迭代异或得到。因此 MT 可以看做一个 $nw-r$ 位的线性反馈移位寄存器，一次 twist 本质上在做 $w$ 次原子化的反馈移位。根据上面我们得到的结论，MT 的周期最大可达 $2^{nw-r}-1$，一组精心设计的参数可以令其达到梅森质数的周期大小，作为参考，MT19937 的参数为：

param mt199937 - 随机数生成算法与其图形应用
图 4-4 MT19937 的参数[13]

基于上述过程，容易发现，MT 的运算大多为简单的加、乘与位运算，对于 CPU 而言这些运算比取模、浮点数与矩阵更快，因此 MT 是高效率的。MT 的周期高达 $2^{19937}-1$，在一般应用中可以不用考虑其周期问题，因此 MT 是性质好的。这就是为什么现在主流的随机数算法都采用了 MT19937，其中包括 C++11 中引入的 std::mt19937。

一个 MT19937 的 C++ 实现可以参见参考资料的 [16]。

Xorshift 随机数生成器

2003 年发明的 Xorshift 随机数生成器系列也基于 LSFR，但并没有 MT 中那么复杂的规则。它通过多次异或移位后的状态来生成随机数，移位的规则需要精心构造才能保证随机数的性质。

例如，下面是一个最简单的 32 位 Xorshift 随机数生成器的 C 源代码[17]：

#include <stdint.h>
​
struct xorshift32_state {
  uint32_t a;
};
​
/* The state word must be initialized to non-zero */
uint32_t xorshift32(struct xorshift32_state *state)
{
    /* Algorithm "xor" from p. 4 of Marsaglia, "Xorshift RNGs" */
    uint32_t x = state->a;
    x ^= x << 13;
    x ^= x >> 17;
    x ^= x << 5;
    return state->a = x;
}

图形学中的随机数：全局光照渲染

随机数的一个应用便是在图形学中广泛存在的蒙特卡洛方法。蒙特卡洛方法通过随机采样对函数的积分值进行估计，从而快速计算出一些不便计算的积分值，且估计的过程可以并行化，便于在 GPU 上计算。

在这一节中将介绍全局光照渲染的光线追踪方法，来展现随机数与蒙特卡洛方法在图形学中的应用。[18][19]

蒙特卡洛方法

蒙特卡洛方法（Monte Carlo Method）是一种通过随机采样进行大量实验，根据实验结果来计算不易计算的积分结构或得到概率分布等。根据大数定理，蒙特卡洛方法在采样数越大的时候，估计结果越接近真实值。

下面以一个例子来理解蒙特卡洛方法。利用蒙特卡洛方法可以求圆周率 π，我们画一个半径为 1、圆心在原点的圆，并取其右上角在 (1, 1) 的外切正方形，接下来在 $(-1,1)^2$ 空间中随机取一些样本点，利用点到圆心的距离判断是否在圆内。假设总样本数为 $n$，在圆内的样本数为 $m$，则圆与外切正方形的面积之比为 $\dfrac{m}{n}$，而 π 可以根据下式求出：

$$ \pi = \dfrac{m}{n} \cdot 2^2 $$

pi sample - 随机数生成算法与其图形应用
图 5-1 利用蒙特卡洛方法求 π 的值[18]

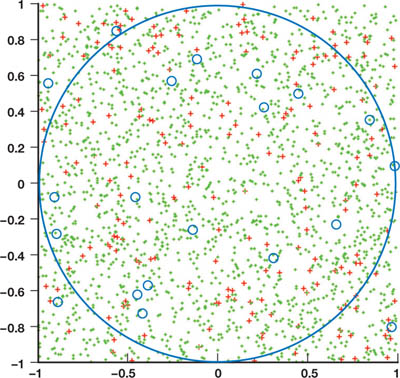
全局光照渲染原理

在本例中，我们只介绍较为简单的模型。

ray trace - 随机数生成算法与其图形应用
图 5-2 环境光渲染示意图[19]

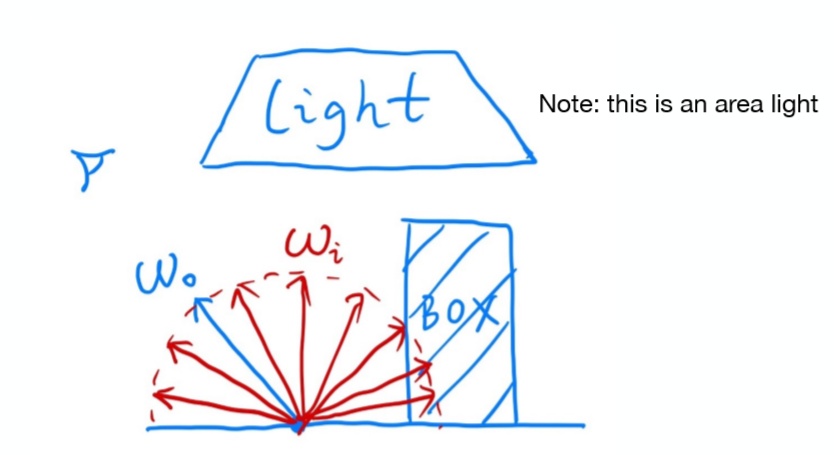
如上图所示，我们想求出观测者观测到给定点 $p$ 的亮度值 $L_o(p, \omega_0)$，其中 $\omega_0$ 为给定点 $p$ 出射到观测者的光线角度。考虑光线入射到 $p$ 点后发生反射，再出射到观测者眼中，则我们可以反着找出哪些入射光可以反射到观测者眼中即可。

给定一个入射角度 $\omega_i$，要找出入射光强 $L_i(p, \omega_i)$ 是简单的，根据光沿直线传播的原理，可以考虑反着求出该光的传播路径，即反着射出一束光，如果路径与某一光源相交，则该光的入射光强可通过光源参数求出。

由于 $p$ 点的反射性质存在漫反射成分，入射角度具有连续的取值区间。假设 $p$ 点自身不发光，则下式可以表示 $p$ 点出射的亮度：

$$ L_o(p,\omega_0) = \int L_i(p,\omega_i)f_r(p,\omega_i,\omega_o) \mathrm{d}S$$

此积分值往往较复杂，在实时渲染中通常采用蒙特卡洛方法快速计算出积分的值。即，从取值区间中取出随机样本，对于每一个角度进行光线追踪，并对所有追踪得到的亮度值求平均叠加。在实际应用中，样本数越多，则积分精度越高，渲染效果越接近理想的物理效果。

GPU 在计算上述流程时，可以并行地生成多组相关度低的随机数作为样本，之后并行地对大量样本进行追踪和计算，随机数生成与蒙特卡洛方法的并行性和高效性在此充分展现出来。

结语

本文的灵感来源为 NVIDIA Developer 上的一篇文章《Efficient Random Number Generation and Application Using CUDA》（参考资料 [18]），该文章启发我学习与研究各种随机数生成算法及其特征，以及文章本身提到的 GPU 上的随机数生成与随机数在图形学中的应用。

随机数是生活中常见的概念，但生活中的随机概念一般基于我们的定性认识。本文尝试从数学与计算机科学的角度研究随机数与其应用，大概介绍了常用的各类随机数与一个随机数在图形学中的应用实例，以期读者能建立对随机数的系统认知。

本文参考了大量网络与文献资料，在此对这些资料的贡献者表示感谢。

参考资料

Author:
Filed Under: 算法, 知识, Slider

2 thoughts on “随机数生成算法与其图形应用”

  • MT19937【多了个⑨
    xorshift的续作xoshiro系列可以提一下
    random.org
    RDRAND指令（以及如何被密码学人拒绝使用）
    以平面取点可视化的话要提一提随机泊松圆盘取点，这个才是专门为平面均匀度设计的
    最后这编辑框为什么键盘左右键被吃（半恼）

    回复

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

此站点使用Akismet来减少垃圾评论。了解我们如何处理您的评论数据。