未完，但是因为退役没机会续了。

前置模板

// Code by KSkun, 2018/7
const double EPS = 1e-8, PI = acos(-1);

inline int dcmp(double x) {
    if(fabs(x) < EPS) return 0; else return x < 0 ? -1 : 1;
}

struct Vector {
    double x, y;
    Vector(double x = 0, double y = 0) : x(x), y(y) {}
    inline Vector operator+(const Vector &rhs) const {
        return Vector(x + rhs.x, y + rhs.y);
    }
    inline Vector operator-(const Vector &rhs) const {
        return Vector(x - rhs.x, y - rhs.y);
    }
    inline Vector operator*(const double &rhs) const {
        return Vector(x * rhs, y * rhs);
    }
    inline Vector operator/(const double &rhs) const {
        return Vector(x / rhs, y / rhs);
    }
    inline bool operator==(const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 && dcmp(y - rhs.y) == 0;
    }
    inline bool operator<(const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 ? dcmp(y - rhs.y) < 0 : dcmp(x - rhs.x) < 0;
    }
    inline bool operator<=(const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 ? dcmp(y - rhs.y) <= 0 : dcmp(x - rhs.x) <= 0;
    }
    inline bool operator>(const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 ? dcmp(y - rhs.y) > 0 : dcmp(x - rhs.x) > 0;
    }
    inline bool operator>=(const Vector &rhs) const {
        return dcmp(x - rhs.x) == 0 ? dcmp(y - rhs.y) >= 0 : dcmp(x - rhs.x) >= 0;
    }
};

typedef Vector Point;

inline double dot(Vector u, Vector v) {
    return u.x * v.x + u.y * v.y;
}

inline double cross(Vector u, Vector v) {
    return u.x * v.y - u.y * v.x;
}

inline double length(Vector v) {
    return sqrt(dot(v, v));
}

inline double angle(Vector u, Vector v) {
    return acos(dot(u, v) / length(u) / length(v));
}

inline Vector rotate(Vector v, double rad) {
    return Vector(v.x * cos(rad) - v.y * sin(rad), v.x * sin(rad) + v.y * cos(rad));
}

struct Line {
    Point p; Vector v;
    Line(Point p = Point(), Vector v = Vector()) : p(p), v(v) {}
};

struct Ray : public Line {
    Ray(Point p = Point(), Vector v = Vector()) : Line(p, v) {}
};

struct Segment : public Line {
    Segment(Point a, Point b) : Line(a, b - a) {}
};

typedef std::vector<Point> Polygon;

struct Circle {
    Point c; double r;
    Circle(Point c = Point(), double r = 0) : c(c), r(r) {}
};

点到直线的射影

算法流程

根据点积的定义，即两个向量的点积等于其中一个向量在另一个向量方向上的投影有向长度乘以另一个向量向量长度。于是我们直接构造向量做点积除以长度即可。

实现

// Code by KSkun, 2018/7
inline Point projection(Line l, Point p) {
    return l.p + l.v * (dot(l.v, p - l.p) / length(l.v));
}

直线与圆的交点

算法流程

联立各自的方程可以得到一个一元二次方程，直接解就好。

实现

这里求得是圆内一点出发的射线与圆的交点。直线的稍微改一改就好。

// Code by KSkun, 2018/7
inline Point intersection(Circle o, Ray l) {
    double x0 = o.c.x, y0 = o.c.y, a = l.p.x, b = l.p.y, c = l.v.x, d = l.v.y;
    double A = c * c + d * d, B = 2 * (a * c - c * x0 + b * d - d * y0), 
        C = a * a - 2 * a * x0 + x0 * x0 + b * b - 2 * b * y0 + y0 * y0 - o.r * o.r;
    double delta = B * B - 4 * A * C;
    double t1 = (-B + sqrt(delta)) / 2 / A, t2 = (-B - sqrt(delta)) / 2 / A;
    if(dcmp(t1) > 0) return l.p + l.v * t1; else return l.p + l.v * t2;
}

转角法、射线法判定点是否在多边形内部

算法流程

对于多边形顶点外的一点P，多边形一条边的转角为该边两点与点P的连线作为角的边，P作为角的顶点构成的一个角。转角可以是钝角、直角或锐角。下图即是AB边对于P的转角$\angle \alpha$的示意图。

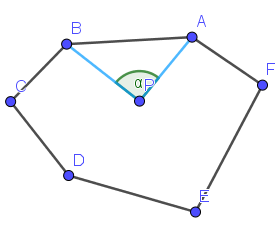
注意，转角是有向角度。为了方便，我们一般规定A→B逆时针的角度为正角，顺时针的角度为负角。
我们发现，当所有边对于点P的转角之和为360°(2π)时，这个点一定在多边形内；如果为0°(0)时，这个点一定在多边形外；如果为180°(π)时，这个点一定在多边形的某条边上（若该点所在边对该点的转角视为0）。下面是三种情况的示意图。
P在多边形内部

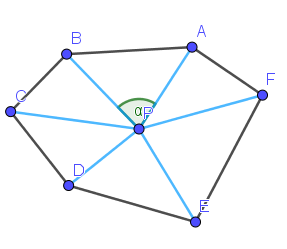
P在多边形某条边上

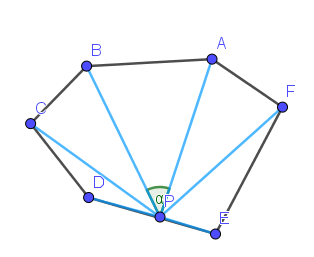
P在多边形外部

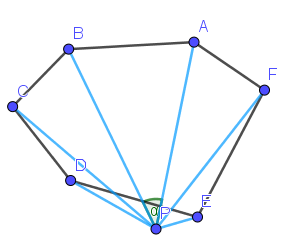
我们发现，这种方法对多边形的限制非常少，它甚至可以用于凹多边形甚至是产生自交的多边形。然而，如果按照上面的方法实现，会产生较大的精度问题，我们一般采用其他方法实现。
下面介绍比较好实现的射线法。
我们假想从P出发有一条水平向右的射线，来统计多边形的边穿过这条射线多少次，若次数为奇数，则在多边形内部，否则在多边形外部。
下面是两种情况的示意图。
P在多边形内部

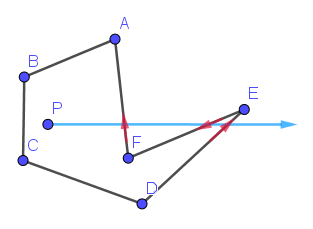
P在多边形外部

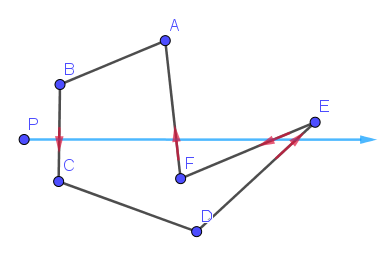
射线法实现

模板题：

• HDU1756 Cupid’s Arrow
• UVa634 Polygon

// Code by KSkun, 2018/7
inline bool onSegment(Segment seg, Point p) {
    Point a = seg.p, b = seg.p + seg.v;
    return dcmp(cross(a - p, b - p)) == 0 && dcmp(dot(a - p, b - p)) < 0;
}

inline int inPolygon(Polygon poly, Point p) {
    int wn = 0; int n = poly.size();
    for(int i = 0; i < n; i++) {
        if(onSegment(Segment(poly[i], poly[(i + 1) % n]), p)) return -1;
        int k = dcmp(cross(poly[(i + 1) % n] - poly[i], p - poly[i])),
            d1 = dcmp(poly[i].y - p.y), d2 = dcmp(poly[(i + 1) % n].y - p.y);
        if((k > 0 && d1 <= 0 && d2 > 0) || (k < 0 && d2 <= 0 && d1 > 0)) wn++;
    }
    if(wn & 1) return 1; else return 0;
}

Andrew算法求二维凸包

算法流程

凸包，是指对于给定点集中的点，最小的以点集中一些点为顶点的能够将点集中所有点包含进来的凸多边形。如下图就是该点集的凸包。

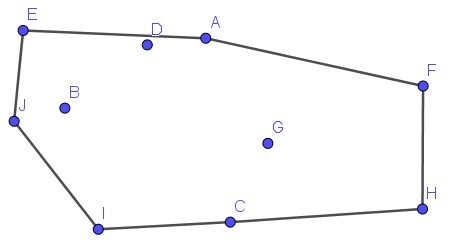
下面介绍基于水平序的Andrew算法。我们把点按横纵坐标双关键字升序排列，从排名最小的点开始找凸包。我们依次加入每个点，定义凸包的前进方向为从倒数第二个加入凸包的点指向最后一个加入凸包的点的向量，则加入每个点之前，要从最近加入凸包的点中依次删除，直到新点在前进方向的左侧。


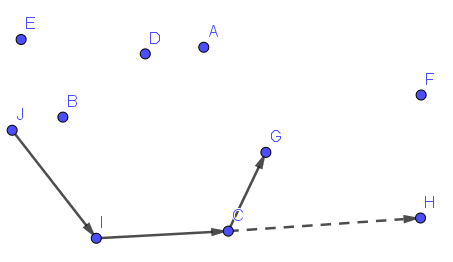
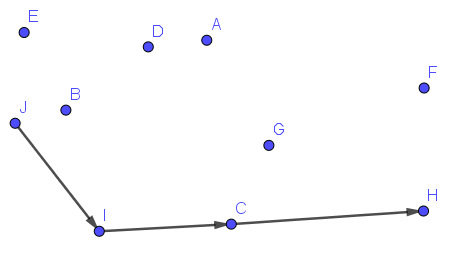
如图，我们正在加入H点的时候，前进方向是$\overrightarrow{CG}$，此时H在这个向量的右侧，所以我们删除G点，前进方向变为了$\overrightarrow{IC}$，可以加入了。

实现

模板题：洛谷2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

// Code by KSkun, 2018/7
inline Polygon convexHull(std::vector<Point> ps) {
    std::sort(ps.begin(), ps.end());
    ps.erase(std::unique(ps.begin(), ps.end()), ps.end());
    Polygon ch; int m = 0;
    for(int i = 0; i < ps.size(); i++) {
        while(m > 1 && dcmp(cross(ch[m - 1] - ch[m - 2], ps[i] - ch[m - 2])) <= 0) {
            ch.pop_back(); m--;
        }
        ch.push_back(ps[i]); m++;
    }
    int k = m;
    for(int i = ps.size() - 1; i >= 0; i--) {
        while(m > k && dcmp(cross(ch[m - 1] - ch[m - 2], ps[i] - ch[m - 2])) <= 0) {
            ch.pop_back(); m--;
        }
        ch.push_back(ps[i]); m++;
    }
    if(ps.size() > 1) ch.pop_back();
    return ch;
}

旋转卡壳

算法原理

首先读好这四个字，旋转卡壳（xuán zhuàn qiǎ ké）。
我们定义一个凸多边形的直径为它顶点中最远点对的距离，旋转卡壳算法就是用来求这个东西的（其实还可以求一些别的奇怪的东西）。
我们来看一下它的原理，如下图（图片来自网络）。

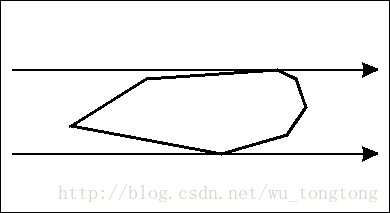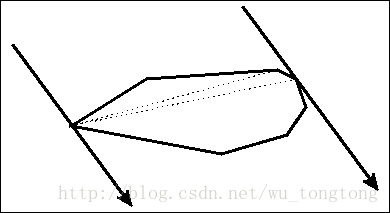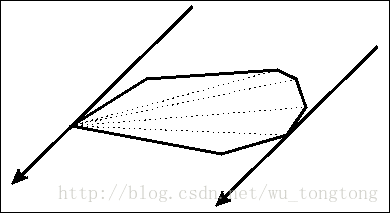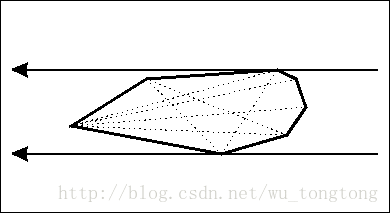
对于这个凸多边形的每一条边，我们找到这条边对面的距离这条边最远的点，而这个点可以通过上图的方式来$O(n)$地寻找。
具体而言，我们知道，以该边两顶点与对面一点构成的三角形面积最大的时候，该点为最远点，而我们发现，移动这条边的时候，最远点也会以同种方式在对面移动，因此我们只需要把这个凸多边形的边遍历一遍就可以找到最远点对的距离了。
在实现上，三角形面积不好找，我们就找第一个在$\overrightarrow{A_uA_{u+1}}$向量右侧的向量$\overrightarrow{A_vA_{v+1}}$就好，这个可以用叉积判断。就是另外要算一下平行的情况，这种情况有两个点到这条边最远。
注：顶点编号顺序是逆时针的。

实现

模板题：POJ2187 Beauty Contest

// Code by KSkun, 2018/7
inline double diameter(Polygon poly) {
    int n = poly.size();
    if(n == 1) return 0;
    if(n == 2) return distance(poly[0], poly[1]);
    double res = 0;
    for(int u = 0, v = 1; u < n; u++) {
        for(;;) {
            double diff = cross(poly[(u + 1) % n] - poly[u], poly[(v + 1) % n] - poly[v]);
            if(dcmp(diff) <= 0) {
                res = std::max(res, distance(poly[u], poly[v]));
                if(dcmp(diff) == 0) res = std::max(res, distance(poly[u], poly[(v + 1) % n]));
                break;
            }
            v = (v + 1) % n;
        }
    }
    return res;
}

参考资料

• 《算法竞赛入门经典 训练指南》，刘汝佳，陈锋著，清华大学出版社，9787302291077
• 旋转卡壳（rotate吧） – CSDN博客