[BZOJ4318]OSU! 题解
题目地址:BZOJ:Problem 4318. — OSU! 题目描述 osu …
May all the beauty be blessed.
题目地址:BZOJ:Problem 2438. — [中山市选2011]杀人游戏
一位冷血的杀手潜入 Na-wiat,并假装成平民。警察希望能在 N 个人里面,查出谁是杀手。警察能够对每一个人进行查证,假如查证的对象是平民,他会告诉警察,他认识的人, 谁是杀手, 谁是平民。 假如查证的对象是杀手,杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手,可看作他们是杀手的概率是相同的。问:根据最优的情况,保证警察自身安全并知道谁是杀手的概率最大是多少?
有$n$个人,其中一个人是杀手,警察知道了每个人认识的人的情况,询问一个人,如果他是平民,则会告诉警察他认识的人的身份,如果是杀手警察会被杀死。现在每个人是平民或杀手的概率是相等的,求在最优情况下,警察安全且得到答案的概率。
输入格式:
第一行有两个整数 N,M。
接下来有 M 行,每行两个整数 x,y,表示 x 认识 y(y 不一定认识 x,例如[一个宽为$w$高为$h$的矩形的面积])。
输出格式:
仅包含一行一个实数,保留小数点后面 6 位,表示最大概率。
输入样例#1:
5 4 1 2 1 3 1 4 1 5
输出样例#1:
0.800000
警察只需要查证 1。假如1是杀手,警察就会被杀。假如 1不是杀手,他会告诉警察 2,3,4,5 谁是杀手。而 1 是杀手的概率是 0.2,所以能知道谁是杀手但没被杀的概率是0.8。
对于 100%的数据有 1≤N ≤ 10 0000,0≤M ≤ 30 0000
首先,对于一个强连通分量里的点,只需要询问分量中一个不是杀手的人,那么这个分量及它连接的分量的信息都可以安全地知道,因此我们可以考虑缩点然后统计入度为0的点有多少个。
然后你就WA了,这是因为,如果$n-1$个点的信息都知道了,那么第$n$个点不用询问也可以知道,可以少冒一次险问一个未知的人。满足这样条件的点一定是在缩点后的新图中大小为1,入度为0且连接的分量入度都不小于2的这样的分量。
那么假如最后求出需要冒险询问的人数是$x$,那么概率就是$\frac{n-x}{n}$。
复杂度$O(n+m)$。
// Code by KSkun, 2018/7
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <set>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1; register char c = fgc();
for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
for(; isdigit(c); c = fgc()) res = res * 10 + c - '0';
return res * neg;
}
const int MAXN = 100005;
int n, m;
std::vector<int> gra[MAXN], gran[MAXN];
int deg[MAXN];
int dfn[MAXN], low[MAXN], clk, sno[MAXN], ssiz[MAXN], scc;
std::stack<int> sta;
bool insta[MAXN];
void tarjan(int u) {
dfn[u] = low[u] = ++clk;
sta.push(u); insta[u] = true;
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
} else if(insta[v]) {
low[u] = std::min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]) {
int p; scc++;
do {
p = sta.top(); sta.pop();
insta[p] = false;
sno[p] = scc;
ssiz[scc]++;
} while(p != u);
}
}
typedef std::pair<int, int> PII;
std::set<PII> edges;
inline bool check(int u) {
if(deg[u] != 0 || ssiz[u] != 1) return false;
for(int i = 0; i < gran[u].size(); i++) {
int v = gran[u][i];
if(deg[v] < 2) return false;
}
return true;
}
int main() {
n = readint(); m = readint();
for(int i = 1, u, v; i <= m; i++) {
u = readint(); v = readint();
gra[u].push_back(v);
}
for(int i = 1; i <= n; i++) {
if(!dfn[i]) tarjan(i);
}
for(int u = 1; u <= n; u++) {
for(int i = 0; i < gra[u].size(); i++) {
int v = gra[u][i];
if(sno[u] != sno[v] && !edges.count(PII(sno[u], sno[v]))) {
gran[sno[u]].push_back(sno[v]);
deg[sno[v]]++;
edges.insert(PII(sno[u], sno[v]));
}
}
}
int cnt = 0;
for(int i = 1; i <= scc; i++) {
if(!deg[i]) cnt++;
}
for(int i = 1; i <= scc; i++) {
if(check(i)) {
cnt--; break;
}
}
printf("%.6lf", double(n - cnt) / n);
return 0;
}
题目地址:洛谷:【P3830】[SHOI2012]随机树 – 洛谷
题面来自洛谷。
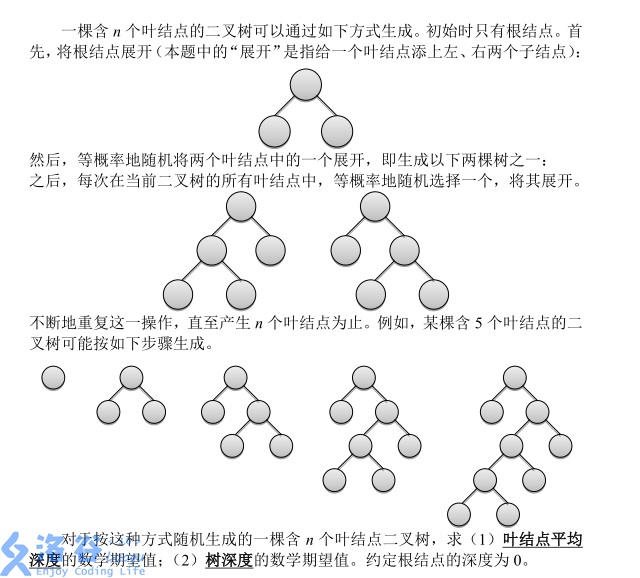
输入格式:
输入仅有一行,包含两个正整数 q, n,分别表示问题编号以及叶结点的个数。
输出格式:
输出仅有一行,包含一个实数 d,四舍五入精确到小数点后 6 位。如果 q = 1,则 d 表示叶结点平均深度的数学期望值;如果 q = 2,则 d 表示树深度的数学期望值。
输入样例#1:
1 4
输出样例#1:
2.166667
输入样例#2:
2 4
输出样例#2:
2.666667
输入样例#3:
1 12
输出样例#3:
4.206421
输入样例#4:
2 12
输出样例#4:
5.916614
2≤n≤100
参考资料:[SHOI2012]随机树 – GuessYCB – 博客园
我们把两个子任务分开看。
第一个求叶节点平均深度的期望,我们令展开i次后这个值为dp[i],则初值dp[1]=0,我们可以利用dp[i-1]来计算dp[i],即将展开的那个叶子节点的深度为dp[i-1],展开后变成了两个dp[i-1]+1深度的叶子,因此转移如下
\begin{aligned} dp[i] &= \frac{dp[i-1] \cdot (i-1) - dp[x-1] + 2(dp[x-1]+1)}{i} \\ &= dp[i-1] + \frac{2}{i} \end{aligned}
由于dp[i]只与dp[i-1]有关,我们甚至不用开数组。
第二个求树高的期望。期望的一种定义是所有情况的和除以情况数,跟展开的情况扯上关系是不好的,因为展开后的形态特别多,没法计算。我们其实并不在意树的形态,而在意树最终有几个儿子,考虑期望的另外一个定义\mathrm{E}(X) = \sum_i \mathrm{P}(X \geq i),我们设计状态dp[i][j]表示有i个叶子的树深度不小于j的概率。转移的时候枚举左子树有多少个叶子,容斥原理计算即可
dp[i][j] = \frac{\sum_{k=1}^{x-1} (dp[k][j-1] + dp[i-k][j-1] - dp[k][j-1] \cdot dp[i-k][j-1])}{x-1}
初始值是dp[i][0]=1。答案就是\sum_{i=1}^{n-1} dp[n][i]。
// Code by KSkun, 2018/4
#include <cstdio>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 105;
int q, n;
double dp[MAXN][MAXN];
int main() {
q = readint(); n = readint();
if(q == 1) {
double res = 0;
for(int i = 2; i <= n; i++) {
res += 2 / double(i);
}
printf("%.6lf", res);
} else {
for(int i = 1; i <= n; i++) dp[i][0] = 1;
for(int i = 2; i <= n; i++) {
for(int j = 1; j < i; j++) {
for(int k = 1; k < i; k++) {
dp[i][j] += dp[k][j - 1] + dp[i - k][j - 1] - dp[k][j - 1]
* dp[i - k][j - 1];
}
dp[i][j] /= i - 1;
}
}
double res = 0;
for(int i = 1; i < n; i++) res += dp[n][i];
printf("%.6lf", res);
}
return 0;
}
题目地址:洛谷:【P3343】[ZJOI2015]地震后的幻想乡 – 洛谷、BZOJ:Problem 3925. — [Zjoi2015]地震后的幻想乡
傲娇少女幽香是一个很萌很萌的妹子,而且她非常非常地有爱心,很喜欢为幻想乡的人们做一些自己力所能及的事情来帮助他们。 这不,幻想乡突然发生了地震,所有的道路都崩塌了。现在的首要任务是尽快让幻想乡的交通体系重新建立起来。
幻想乡一共有n个地方,那么最快的方法当然是修复n-1条道路将这n个地方都连接起来。 幻想乡这n个地方本来是连通的,一共有m条边。现在这m条边由于地震的关系,全部都毁坏掉了。每条边都有一个修复它需要花费的时间,第i条边所需要的时间为ei。地震发生以后,由于幽香是一位人生经验丰富,见得多了的长者,她根据以前的经验,知道每次地震以后,每个ei会是一个0到1之间均匀分布的随机实数。并且所有ei都是完全独立的。
现在幽香要出发去帮忙修复道路了,她可以使用一个神奇的大魔法,能够选择需要的那n-1条边,同时开始修复,那么修复完成的时间就是这n-1条边的ei的最大值。当然幽香会先使用一个更加神奇的大魔法来观察出每条边ei的值,然后再选择完成时间最小的方案。 幽香在走之前,她想知道修复完成的时间的期望是多少呢?
输入格式:
第一行两个数n,m,表示地方的数量和边的数量。其中点从1到n标号。 接下来m行,每行两个数a,b,表示点a和点b之间原来有一条边。 这个图不会有重边和自环。
输出格式:
一行输出答案,四舍五入保留6位小数。
输入样例#1:
5 4 1 2 1 5 4 3 5 3
输出样例#1:
0.800000
提示:
(以下内容与题意无关,对于解题也不是必要的。)
对于n个[0,1]之间的随机变量x1,x2,…,xn,第k小的那个的期望值是k/(n+1)。
样例解释:
对于第一个样例,由于只有4条边,幽香显然只能选择这4条,那么答案就是4条边的ei中最大的数的期望,由提示中的内容,可知答案为0.8。
数据范围:
对于所有数据:n<=10, m<=n(n-1)/2, n,m>=1。
对于15%的数据:n<=3。
另有15%的数据:n<=10, m=n。
另有10%的数据:n<=10, m=n(n-1)/2。
另有20%的数据:n<=5。
另有20%的数据:n<=8。
题目要求最小生成树上的最大边权Y的期望,因此我们只需要关心这个最大边权在所有边权中的排名,我们发现有下面的式子
\mathrm{E}(Y) = \sum_{i=1}^n \mathrm{E}(i)\mathrm{P}(i) = \sum_{i=1}^n \frac{i}{m+1} \cdot \mathrm{P}(i) = \frac{\sum_{i=1}^n i\mathrm{P}(i)}{m+1} = \frac{\mathrm{E}(Z)}{m+1}
最后我们发现要求的就是最小生成树上最大边权排名的期望值Z。考虑怎么求这个Z,设L为同定义的随机变量,有
\mathrm{E}(Z) = \sum_{i=1}^m i\mathrm{P}(L=i) = \sum_{i=1}^m \mathrm{P}(L \geq i)
如果说最大边排名大于等于i不好求,我们就正难则反,求排名小于i的边集无法构成生成树的概率,由于所有的边权都是随机分布的变量,这个概率可以转化为从边集中随机选择i条边无法构成生成树的概率,我们考虑计算出选择i条边无法构成生成树的方案数,进而计算概率。
通过观察题目数据范围,我们发现n的范围很适合状压。考虑状压DP,用f[S][i]表示在S点集构成的子图中,选i条边使得该点集不连通的方案数,这个状态似乎没法转移,但是我们考虑与其意义互补的量:g[S][i]表示在S点集构成的子图中,选i条边使得该点集连通的方案数,显然有
f[S][i] + g[S][i] = \mathrm{C}_{ecnt[S]}^i
ecnt表示该点集构成子图内的边数。如果知道了其中一个,我们就可以知道另外一个。那么怎么转移成了问题,我们考虑固定S中的某个点,对于S这个点集的一个包含定点的真子集T,只要使T连通但\complement_S T与T之间没有连边就能保证S不连通了,而枚举每一个T可以实现对S不连通情况的遍历。最后我们的转移式就是
f[S][i] = \sum_{T \subsetneqq S, U \in T} \sum_{j=0}^{ecnt[T]} g[T][j] \cdot \mathrm{C}_{ecnt[\complement_S T]}^{i-j}
最后,我们获得了 \mathrm{E}(Z) = \sum_{i=0}^{n-1} f[\mathbb{U}][i] ,直接计算答案即可。
注意爆int。
需要证明的内容:对于n个[0,1]之间的随机变量x1,x2,…,xn,第k小的那个的期望值是k/(n+1)。
我们首先令x_1为第k小值,我们现在来求它的期望。
对于这种情况,我们显然有其中k-1个值比它小,n-k个值比它大,我们分别计算概率,乘起来,就得到了概率密度,对其积分就是x_1为第k小值时x_1的期望值,即\mathrm{E}(x_1, x_1是第k小数)
\begin{aligned} & \int_0^1 x_1 \cdot x_1^{k-1} (1-x_1)^{n-k} \mathrm{d}x_1 \\ = & \int_0^1 x_1^k (1-x_1)^{n-k} \mathrm{d}x_1 \\ = & \mathrm{B}(k+1, n-k+1) \\ = & \frac{k!(n-k)!}{(n+1)!} \end{aligned}
我们知道了这个,但是要求的是E(第k小数),即\mathrm{E}(x_1|x_1是第k小数)。我们记x_1是第k小数这一事件为A,根据下面的关系
\mathrm{E}(x_1|A) = \frac{\mathrm{E}(x_1, A)}{\mathrm{P}(A)}
我们又容易知道
\mathrm{P}(A) = \frac{1}{n \cdot \mathrm{C}_{n-1}^{k-1}}
直接就可以算出来了,结果就是
\mathrm{E}(x_1|A) = \frac{k}{n+1}
// Code by KSkun, 2018/3
#include <cstdio>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
const int MAXN = 13, MAXM = 50;
int n, m, ut, vt;
LL gra[MAXN], cnt[1 << MAXN], ecnt[1 << MAXN], f[1 << MAXN][MAXM], g[1 << MAXN][MAXM];
LL C[MAXM][MAXM];
inline void calc() {
for(int i = 0; i <= m; i++) {
C[i][0] = 1;
for(int j = 1; j <= i; j++) {
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
int main() {
n = readint(); m = readint();
calc();
for(int i = 0; i < m; i++) {
ut = readint(); vt = readint();
gra[ut] |= (1 << (vt - 1));
gra[vt] |= (1 << (ut - 1));
}
for(int i = 0; i < 1 << n; i++) {
cnt[i] = cnt[i >> 1] + (i & 1);
}
for(int i = 0; i < 1 << n; i++) {
for(int j = 1; j <= n; j++) {
if(i & (1 << (j - 1))) {
ecnt[i] += cnt[gra[j] & i];
}
}
ecnt[i] >>= 1;
}
for(int i = 0; i < 1 << n; i++) {
if(cnt[i] == 1) {
g[i][0] = 1;
continue;
}
int t = i & (-i);
for(int j = (i - 1) & i; j; j = (j - 1) & i) {
if(j & t) {
for(int k1 = 0; k1 <= ecnt[j]; k1++) {
for(int k2 = 0; k2 <= ecnt[i ^ j]; k2++) {
f[i][k1 + k2] += g[j][k1] * C[ecnt[i ^ j]][k2];
}
}
}
}
for(int j = 0; j <= ecnt[i]; j++) {
g[i][j] = C[ecnt[i]][j] - f[i][j];
}
}
double ans = 0;
for(int i = 0; i <= m; i++) {
ans += double(f[(1 << n) - 1][i]) / C[m][i];
}
printf("%.6lf", ans / (m + 1));
return 0;
}